空腹楼盖在工程实际应用中的配筋分析

曹文泽

（贵州理工学院土木工程学院 ，贵州 贵阳 550003）

0 引言

磷石膏膜壳空腹楼盖采用石膏模盒，在楼盖施工中作为填充内模，施工结束后，石膏空腔模与混凝土层合成一体，形成现浇混凝土石膏空腔模空腹楼盖[1]。空腹楼盖因其良好的力学性能[2]、保温性能和经济性能，在工程应用中逐渐增多，把工业废料磷石膏制成膜壳内置于楼板内还能进一步利用工业废料[3]，减少环境污染。目前空腹楼盖在工程应用中大多数是密肋式空腹楼盖[4]，而更多性能更优新型空腹形式楼盖因设计者对其配筋方式不够了解，在工程实际中应用不够广泛。

文献[5]以拓扑分析[6]结果为基础，提出了两类施工便利、经济节约、受力性能更好的新型空腹楼盖形式。两类空腹楼盖的具体构造及尺寸如图1所示，两类楼盖的差异在于内部剪力传递部分的布置形式不同。空腹板架式无梁楼盖内部剪力健分布均匀，能够较好的协调空腹板的上下两层面板，9区格式无梁楼盖内部肋梁布置连续，内部形成较大的空腔，在施工上便于操作。

图1 结构平面图

目前在工程实际应用中，尚无专门针对空腹楼盖配筋设计的软件，部分软件虽然含有空腹楼板的配筋设计功能，但该功能只局限于普通的密肋式空腹楼盖。本文以图1中两类新型空腹楼盖形式为例，具体分析非常规空腹楼盖的实际应用配筋方式。

1 原理介绍

楼板在竖向荷载作用下，截面上既有由弯矩引起的正应力σ，又有剪切应力τ，但一般情况下，剪切应力对板的强度和变形为次要因素。非常规空腹楼盖在设计配筋上可按照刚度等代原理等代为常规楼板进行设计。板楼板刚度等代原理可分为剪切刚度等代和抗弯刚度等代。楼盖弯刚度的表达式为D=EI（E：材料弹性模量，I：截面惯性矩），故对于抗弯刚度等代只需要等代截面抗弯刚度相同即可。楼盖剪切刚度表达式为C=GA（G：材料剪切模量，A：截面面积），故对于剪切刚度等代只需要面积相同即可。

2 等代计算

由于剪切应力对于楼板强度和变现为次要因素，一般情况下楼板不会出现抗剪破坏，对于剪切应力不满足部位，可在板柱节点位置布置柱帽或在节点附近布置暗梁等形式以增加截面面积解决。而楼板设计主要是根据竖向荷载下的弯矩来计算配筋，对于空腹板架式无梁楼盖，由于内部肋梁分布规律，只需要取肋梁宽度楼板来进行刚度等代计算如图2-a所示。先求出空腹板的截面形心，对截面型心求矩，根据I1=I2即可求出等代实体板厚度H2。对于9区格式无梁楼盖由于内部梁分布无规律，刚度等代时只算入上下两层板如图2-b所示。先求出空腹板的截面形心，对截面型心求矩，根据I1=I2即可求出等代实体板厚度H2。

图2 抗弯刚度等代示意图

3 受力分析

计算得到楼板等代厚度后，即可把非常规空腹板当成普通楼板在常规设计软件中进行建模分析。常规的设计软件如SLABCAD等软件都可进行楼板内力、配筋计算。本文以图1所示楼板跨度为例，在软件中建立模型，按实际设置材料属性，并输入楼板承受的恒、活荷载，在输入恒载时要考虑因刚度等代造成的楼板厚度不同的影响。

软件分析结束后，可以得到板的内力分布以及楼板挠度情况。因空腹楼板的配筋不同于普通实体板，我们只能利用软件分析出内力，然后利用内力人为进行配筋。楼板受力后在跨中为正弯矩，底部受拉，支座附近为负弯矩，顶部受拉；故在分析时我们需要提取楼板面部与底部的弯矩。在应用上通常楼板尺寸多为矩形，及在两边上尺寸不一，故对楼板的面部和底部弯矩需区分X向和Y向。本例中因楼板具有双向对称性，故截取了楼板1/4部分的力学分析结果如图3所示。从分析结果可以看出板面负弯矩只有在支座附近才出现，板底正弯矩在跨中出现，这与楼板实际受力情况相符。

图3 楼板弯矩（kN.m/m）

4 楼板配筋

通过分析，可得到的弯矩值即为空腹板在受力情况下的弯矩。知道弯矩即可利用混凝土配筋计算式对楼板进行配筋计算，配筋时还需结合现行规范进行配筋。两类空腹楼盖的配筋构造如图4所示。空腹板架式无梁楼盖内部剪力健和小肋梁分布均匀，上层板的跨度不大只配置一层钢筋；而9区格式无梁楼盖上层板的跨度较大，在受力时区格中部会出现正弯矩，需配置两层钢筋。

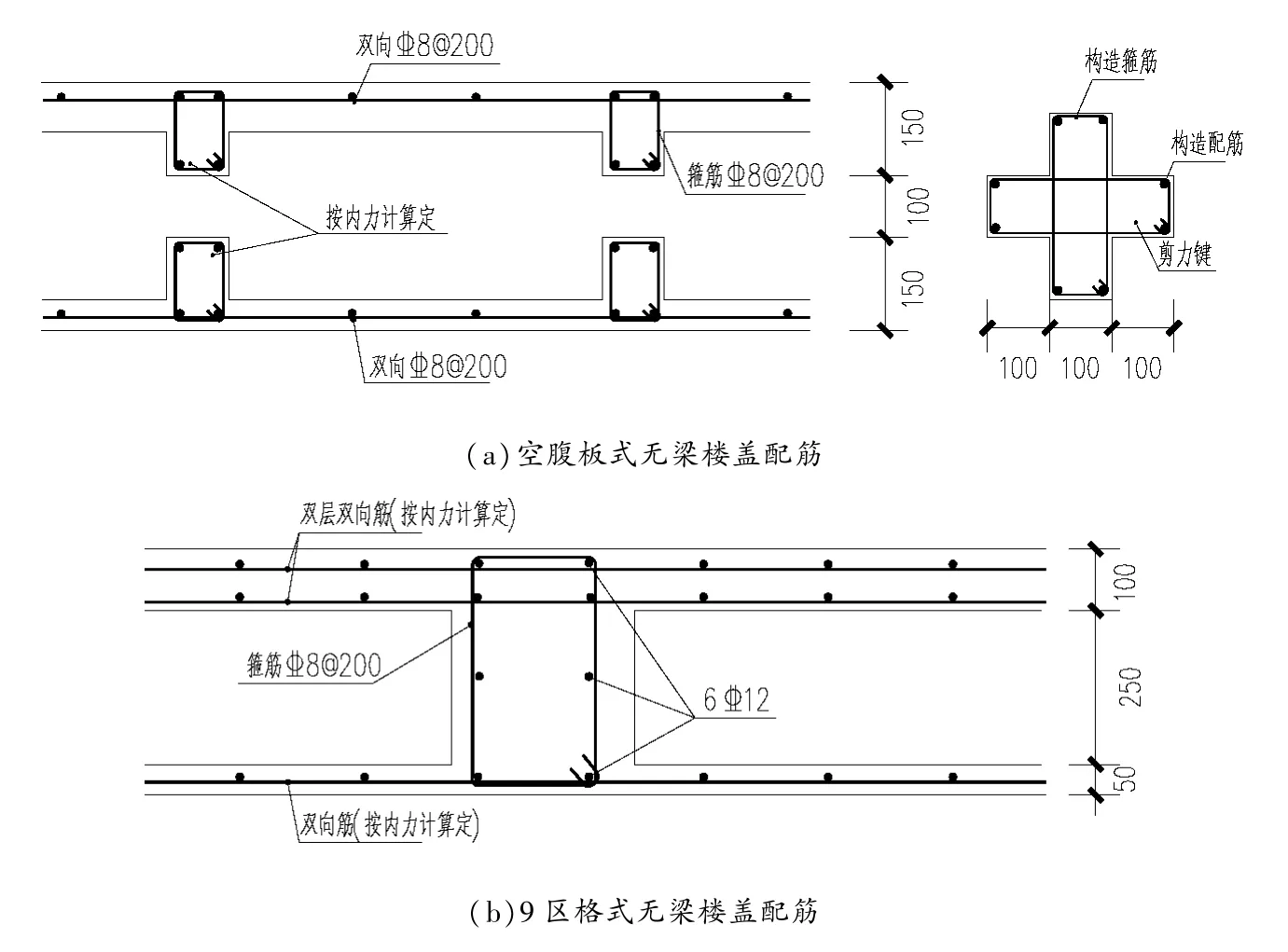
图4 配筋示意图

5 结论

本文以空腹板架式无梁楼盖和9区格式无梁楼盖为例，讨论了非常规空腹板配筋的方法及过程。非常规空腹板在工程应用上还没广泛使用，对于其配筋还未有成熟的专用软件来设计，只能用现有设计软件和力学分析来进行设计，在配筋上还需空腹板内部构造来考虑配筋构造。以上配筋方法在实际应用上简单易行，可结合常用的结构设计软进行整体建模，既不影响结构整体分析，又可对空腹板配筋进行分析，可为空腹楼板设计配筋提供参考。