固体结构内部瞬态非均匀温度场的重建方法研究
2017-01-07石友安魏东桂业伟钱炜祺曾磊刘骁
石友安, 魏东, 桂业伟, 钱炜祺, 曾磊, 刘骁
(1.中国空气动力研究与发展中心 空气动力学国家重点实验室, 四川 绵阳 621000;2.中国空气动力研究与发展中心 计算空气动力学研究所, 四川 绵阳 621000)
固体结构内部瞬态非均匀温度场的重建方法研究
石友安1,2, 魏东2, 桂业伟2, 钱炜祺2, 曾磊2, 刘骁2
(1.中国空气动力研究与发展中心 空气动力学国家重点实验室, 四川 绵阳 621000;2.中国空气动力研究与发展中心 计算空气动力学研究所, 四川 绵阳 621000)
固体结构内部瞬态非均匀温度场的无损测量在航空航天、机械制造、材料加工和医疗卫生等领域都具有十分重要的作用。基于超声波脉冲回波法,建立了超声测量各向同性均匀介质结构内部瞬态温度分布的理论模型,发展了预测结构内部非均匀温度场的灵敏度法和共轭梯度法,并系统比较分析了两种瞬态温度场重建算法的精度、抗噪性和稳定性等特性。实验验证表明:基于热传导反问题的两种方法,重建得到的结构内部瞬态非均匀温度分布精度均较高,实时性好,适用性强;对结构内部瞬态温度场的预测与评估以及探索研究结构内部量的新型测量和控制技术等具有参考意义。
兵器科学与技术; 瞬态温度场; 超声测温; 温度场重建; 灵敏度法; 共轭梯度法
0 引言
温度作为一个基本物理量,是确定介质状态最重要的参数之一。结构内部瞬态温度场的测量在航空航天、机械制造、材料加工和医疗卫生等领域都具有十分重要的作用[1-2]。目前,结构内部的温度测量主要采用内埋传感器(譬如热电阻、热电偶)的接触式探测,但这种方法有一些局限性,如打孔安装传感器容易破坏结构的原有形态,并可能导致结构局部的温度变化或产生应力集中等问题。无损非接触式测温方法中的红外技术、磷光热图等目前还仅适用于结构表面温度的测温[3-4]。因此,发展应用范围更广的无损温度测量技术成为目前固体结构内部温度测量与控制中亟待解决的热点之一。
超声波测温技术可以实现对结构内部温度场的无损非接触式探测。相比传统的测温方法,超声波测温具有更快速、更精确、使用范围更宽的优势[5-6],且已经在气体、液态材料等方面取得一系列研究成果。但是,对于探测固体结构内部瞬态温度场的研究还比较少,需要进一步研究诸如纳秒级声时测量技术、瞬态温度场重建的数理模型和多参数的反演计算方法等关键技术问题[7-8]。
本文从热声学理论和超声测温感知机理[9-10]出发,建立了结构内部瞬态非均匀温度场非接触探测的理论模型;从求解反问题角度入手,将瞬态非均匀温度场的重建问题转化为热边界的反演和热传导正问题的求解;应用参数辨识中的灵敏度法和共轭梯度法,发展了基于求解热传导反问题的结构内部瞬态温度场重建技术,并开展了一系列的数值仿真分析和有效性验证,得到了一些有意义的结果。
1 超声测温模型
如图1所示,假设一均质结构左端受到沿空间均布的时变热流加热。结构内部的非均匀温度场沿其受热面垂直方向可视为一维分布状态,即结构内部各点的温度值仅是x的函数。超声测温中声波探头安装在结构右端。采用脉冲回波法进行测量时,超声波在固体介质中的传播时间ttof[11]可表示为

(1)
式中:T为温度;L为超声波在固体介质中单向传播的距离(被检测结构的厚度);v是固体介质中超声波的传播速度,与材料性能和结构所受温度相关。

图1 超声测温的一维模型Fig.1 One-dimensional model of ultrasound speed measurement of temperature
在各向同性介质中,v通常可以表示为结构所受温度的线性函数,如
v(T)=mT+n,
(2)
式中:m和n为常数,由实验标定得到。
固体介质中的温度T,其一维情况下可以表示为位置x和时间t的函数,显然T(x,t)即为待求的一维结构内部非均匀温度场分布状态。
图2描述了钢中超声波纵波的传播速度与温度的变化关系[12]。
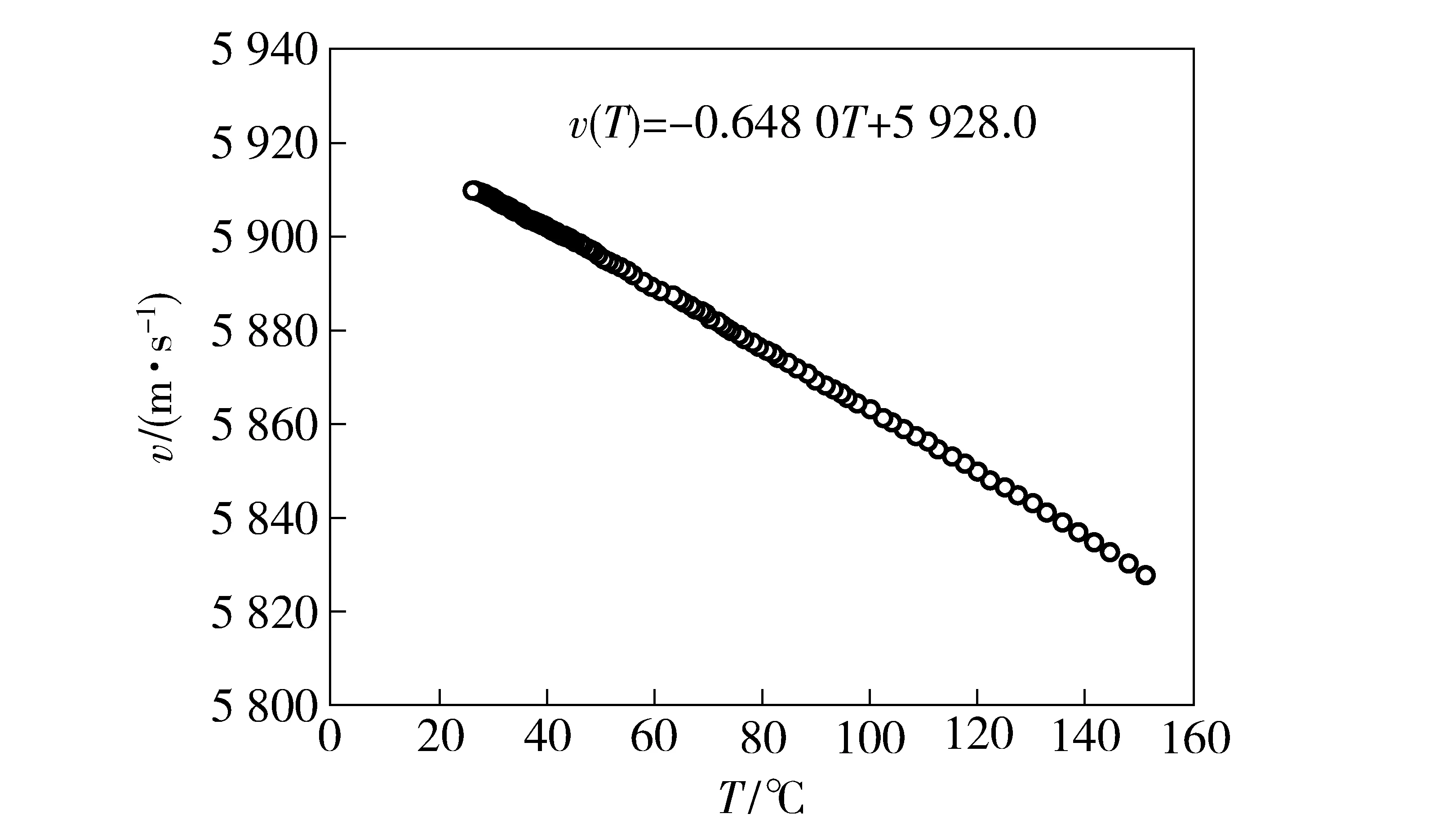
图2 钢中纵波波速与温度的关系Fig.2 Longitudinal wave velocity vs, temperature in steel
因此,基于超声波波速与温度的相关性,首先采用超声波脉冲回波法,准确获得超声波在固体介质中的传播时间ttof. 然后,基于参数反演,根据(1)式以及声波传播速度与介质温度的函数关系反演出等效的边界条件。最后,基于热传导的正问题求解获得结构内部不同时刻的温度场分布状态。
2 瞬态温度场的反演算法
基于传播时间进行温度场的重建,本质上是一个热- 声- 固体耦合的反问题。对于一维温度场重建而言,可暂不考虑超声波传播路径的变化。
一维无内热源热传导正问题可描述为
主控方程

(3)

T|x=L=Tcons,
初值条件T|t=0=Tcons,
观测方程
ttof,m=ttof,ex+εtof,m,
(4)
式中:Ttop为待反演的温度边界;Tcons为恒定温度值;k为导热系数;ρ为密度;cp为比热容;q为热流密度;ε为测量误差;t为时间;下标“m”表示测量得到,下标“ex”表示精确值。反问题描述为:已知测量的超声波传播时间ttof(见(4)式),求解主控方程中的边界热流q(t)或Ttop.
反演算法思路:以传播时间为依据,在数值求解正问题的基础上,根据输出误差原则,将反问题转化为一个优化问题,等价于寻求合适的函数q(t)(或者Ttop),使目标泛函J达极小值的过程:

(5)
式中:下标“c”表示计算得到。边值条件q(t)或Ttop的反演估计中,目标函数J(q(t))设定后,则物理系统参数反分析问题就可以归结为求解如下非线性优化问题:
minJ(q(t)),

T(x,t),t>0,x∈[0,L].
(6)
2.1 灵敏度法
灵敏度法[13]的描述如下:目标函数达到极小的必要条件为∂J(θ)/∂θ=0,θ是待辨识参数,当在第i迭代层次上Ji(θi)不是极小值时,必须调整θi使Ji+1达到极小值,则有

(7)
略去2阶以上小量后得


(8)
式中:M称为信息矩阵。向量∂J/∂θ和矩阵M中都含有状态变量对参数的导数,该导数称为灵敏度,由(8)式构成的算法称之为灵敏度法。对于稳态边界,信息矩阵则退化为单一元素;对于瞬态边界,则为n×n矩阵。由于热传导方程的扩散性,n×n矩阵多为病态矩阵[14]。
因此,在本文中,灵敏度法主要用于稳态边界Ttop的反演。根据变分原理,对目标函数取变分,得到目标函数关于待辨识边界的导数为

(9)
对(9)式再求导,则得到信息矩阵为

(10)
式中:∂T/∂Ttop为温度场关于待辨识加热边界的灵敏度。将主控方程(3)式关于待辨识边界求导即可得到灵敏度方程。优化步骤见(8)式。
2.2 共轭梯度法
共轭梯度法也称为迭代正则化方法[15-16],分解为热传导正问题、灵敏度问题和伴随变量问题进行求解。优化算法[15]描述如下:
(11)

为了得到伴随方程,引入伴随变量λ,将目标函数(5)式写为如下的扩展形式:

(12)
对(12)式右边第二部分做分部积分后再做变分,得到伴随方程为

(13)

(14)
步长由(15)式计算:

(15)
式中:Δttof是Δq=Pn引起的传播时间的变化值。在优化过程中,收敛准则根据输出误差原则获得
J<δ,δ=Mmσ2,
(16)
式中:Mm为测量点数。至此,梯度、步长均已求出,共轭梯度可由梯度、步长构造。具体优化过程可参阅文献[17]。
3 精度、抗噪性和稳定性分析
本节通过数值仿真,分析两种反演算法的精度、抗噪性以及稳定性等。
数值仿真中,假定超声波波型为纵波,介质材料为钢,长度5 cm. 钢中纵波波速与温度的关系见(17)式。通过计算相应的正问题获得超声波传播时间ttof的真值。
v(T)=-0.648 0T+5 9280.0.
(17)
首先,针对灵敏度法开展仿真分析。假设加热面温度为350 K,计算时间为60 s. 为了更好地模拟实际测量数据,在精确时间的基础上,分别叠加标准差为0,均方差σ为1×10-7s、5×10-7s、1×10-6s和5×10-6s的白噪声作为模拟传播时间。表1给出了超声波传播时间叠加不同噪声情况下加热边界的辨识结果对比。
图3给出了距加热面15 mm测点处辨识的温升对比。从图3中可以发现,随着信噪比的降低(噪声的增大),辨识精度下降,相对温升的误差增长较快。例如无白噪声时,温升相对误差(即加热面温度辨识值与实际值的比值)为0.000 3%;叠加5×10-7s的白噪声后,相对误差约为1.67%. 由此可以看出,灵敏度算法具有较好的抗噪性。

表1 灵敏度法辨识的温度边界结果对比Tab.1 Comparison of boundary temperatures estimated by sensitivity method

图3 采用灵敏度法反演的测点处温升历程对比Fig.3 Temperature variation at measurement point estimated by sensitivity method
接着,通过典型热流的反演,分析共轭梯度法的精度和抗噪性等。
边界热流为正弦和阶跃热流,计算时间为5 s. 通过计算相应的正问题,得到模拟传播时间。在实际应用中,误差不可避免。因此,在模拟值的基础上分别叠加标准差为1×10-8s、1×10-9s和1×10-10s的白噪声作为实际测量值,具体见图4. 从图4中可以发现,超声波的传播时间非常短暂,为微秒量级;相较于传播时间总的变化值(约0.11×10-6s),1×10-8s的误差标准差相当于带来了近10%的敏感度误差。

图4 模拟的传播时间Fig.4 Simulated transit time of ultrasonic wave
图5显示基于超声传播时间,采用共轭梯度法反演得到的热流值对比情况。从图5中可以发现,在非连续点处,辨识值存在一定的“数值振荡”,如阶跃热流的阶跃点;此外,在起始点和尾点处与模拟真值还存在一定的差异。除此之外,随着误差的减小,辨识值与模拟真值的吻合度增加;当误差标准差为1×10-8s时,两种热流的反演值均较差,这主要与信号的信噪比过小有关;当误差标准差为1×10-9s时,正弦热流反演值的偏差带约为±5%,阶跃热流反演值的偏差带约为±10%;当误差标准差为1×10-10s时,正弦热流反演值的偏差带约为±3%,阶跃热流反演值的偏差带约为±5%. 起始点处、尾点处与真值的差异,主要是与起始点处灵敏度较小,尾点处伴随变量始终为0有关(可参见第2节中的(13)式)。起始点处的灵敏度较小,是由热传导过程的扩散特性决定的,修正较为困难;尾点处的辨识值较差可以通过修正伴随变量而改善,如λtmax=λtmax-1.

图5 采用共轭梯度法反演的热流值对比Fig.5 Comparison of heat fluxes estimated by conjugate gradient method
图6显示了基于反演的热流重建得到的典型时刻温度分布的对比情况。从图6中可以发现:最大偏差出现在热边界处,除此之外,计算值与模拟真值吻合较好;随着误差的增加,偏差增大;5 s时刻,当白噪声的标准差为1×10-8s时,正弦热流边界的温度最大偏差55 ℃(起始点处),约10%,而阶跃热流边界的最大偏差为75 ℃,约12%;1×10-9s时,正弦热流的最大偏差降为45 ℃,约8.8%,阶跃热流则降为30 ℃,约6%;1×10-10s时,正弦热流的温度最大偏差急剧减小至10 ℃,约2%,阶跃热流则降为5 ℃,约1%. 最大偏差出现在起始点处,主要是与该点的灵敏度较小有关。

图6 重建的不同时刻温度分布对比Fig.6 Comparison of reconstructed temperature distributions at different time
通过上述分析,不难发现,为了保持重建的温度场具有较好的精度,传播时间的精度需要保持1×10-9s量级。结合(17)式可知,纵波在钢中传播时,温度变化1 ℃,波速变化0.648 m/s. 传播时间与传播路径长度和波速有关。在本算例中,材料长度为5 cm,则材料的温度变化1 ℃,传播时间变化约1.8×10-9s. 由此可见,超声波对于结构内部温度的敏感度非常微弱。这对测试信号的信噪比和重建算法的抗噪性提出要求。
最后,分析一下算法的稳定性。热传导反问题是一个不适定的问题,体现在解不连续依赖于数据,即观测数据的细微误差可能导致巨大变化。要克服这种不适定性,通常的做法是对目标函数正则化,使不适定性问题变为适定。
正则化主要有两种方法,一种是Beck[10]的正则化方法,另一种是文献[18]中Alifanov的迭代正则化方法,通过设定合适的收敛准则来达到正则化的目的,例如,本文的(16)式。该方法实现方便,适于工程应用。
定义辨识值与真值之间的相对偏差E为

(18)
式中:下标“av”表示平均值。
定义计算传播时间与测量值之间的平均偏差S为
(19)
从图7可以看出:在反演过程中,E的极小值并非出现在J的极值处,而是某一局部值处,约Mmσ2,即(16)式。E与J关系实质上是输出误差原则的体现,只要合理的利用这种关系就可以使算法具有良好的抗噪性与稳定性。

图7 E随目标函数J下降的变化关系Fig.7 Variation of E with objective function J
综上可知,基于灵敏度法和共轭梯度法建立的固体结构内部瞬态温度场的反演方法,精度较高、抗噪性较好,并且具有可靠的稳定性。
4 算法验证
为了进一步分析算法的有效性,本节借鉴文献[19]中的实验数据,进行两种算法的有效性验证。实验示意如图8所示。

图8 文献[19]实验示意图Fig.8 Schematic diagram of experimental setup for ultrasonic temperature monitoring in Ref. [19]
测试材料为不锈钢,长度为30 mm. 底部采用75 ℃热水加热10 s,其他边界可以近似为绝热。为了对比分析超声测温数据,在试件内部的长度方向,均布5个热电偶。初始温度为26 ℃. 试件中超声波的波速与温度的关系式为
v(T)=-0.648T+5 934.9.
(20)
图9给出了超声波传播时间的计算值与文献[19]实验测量值的对比。从图9中可以发现:对于共轭梯度法而言,传播时间计算值的变化趋势与测量值吻合非常好,最大偏差小于0.1%;对于灵敏度算法而言,6 s前,计算得到的传播时间偏大,偏差随时间增加而减小;6 s后,计算值偏小,偏差随时间增加而增大;全时间域内平均偏差小于0.5%. 分析认为,在共轭梯度法中,反演的热边界为瞬态,更符合实验中加热边界的物理描述,而在灵敏度算法中,反演的热边界为稳态,若物理边界为瞬态,则是一种等效近似处理。

图9 渡越时间计算值与文献[19]对比Fig.9 Comparison of estimated transit time of ultrasonic waveand that in Ref.[19]
图10给出了不同时刻温度分布的重建值与文献[19]测量值的对比。从图10中可以发现,采用共轭梯度法重建的温度分布与热电偶的测量值吻合得最好;对于灵敏度算法而言, 5 s时刻的重建精度高于文献[19]中的重建算法,接近共轭梯度法,但是1 s、和2.6 s的精度则最差;距离加热边界越近,重建误差越大,在热电偶1点处,共轭梯度的偏差小于0.1 ℃,灵敏度法约1 ℃,而文献[19]中的算法则为2.2 ℃. 由此可见,共轭梯度法具有较高精度,且适用性较好,而灵敏度算法受限于稳态边界限制,适用范围有限。

图10 重建的不同时刻温度分布值与文献[19]测量值对比Fig.10 Comparison of reconstructed temperature distribution at different time and those in Ref.[19]
图11给出了不同测点的温升历程与测量值的对比。从图11中可以发现:5 s时刻,采用共轭梯度法重建得到的温升历程与测量值吻合最好,最大偏差小于0.1 ℃,灵敏度法与文献[19]中的重建算法精度相当,最大偏差约2.2 ℃;对于1 s和2.6 s时刻,采用灵敏度法重建得到的温升历程与测量值吻合得最好,最大偏差小于0.1 ℃,共轭梯度法与文献[19]中的重建算法精度相当,最大偏差约0.3 ℃. 这主要是因为1 s和2.6 s时刻,加热时间太短,热边界可以近似为稳态,而共轭梯度法由于初始时刻灵敏度较小,重建精度略受影响。

图11 不同测点处温升历程与文献[19]测量值对比Fig.11 Comparison of estimated temperature histories at different measuring points and those in Ref.[19]
为了增强灵敏度算法的适用性,本文针对灵敏度算法,采用准定常近似处理,分段重建结构内部瞬态温度分布。图12给出了采用准定常近似后,传播时间计算值与文献[19]测量值的对比。从图12可以发现,采用准定常近似后,传播时间随时间的变化趋势与测量值的吻合度增加。

图12 准定常修正后传播时间计算值与文献[19]测量值对比Fig.12 Comparison of quasi-steady corrected estimated transit time of ultrasonic wave and that in Ref.[19]
图13给出了采用准定常近似后不同测点的温升历程与测量值的对比。从图13中可以发现,采用准定常近似后,采用灵敏度算法重建的温度分布的精度得到了有效的改善,其精度接近于共轭梯度法。图14给出了共轭梯度法反演得到的热流。从图14可以清晰地分辨出热边界几乎保持为一个恒定值,符合物理实际。起点处和尾点处的热流值偏低,这主要与起始点处灵敏度较小,尾点处伴随变量始终为0有关。这两个点的反演值受初值影响较大。

图13 准定常近似后不同时刻温度分布值与文献[19]测量值对比Fig.13 Comparison of quasi-steady corrected temperature distributions at different time and those in Ref.[19]

图14 共轭梯度法反演得到的热流Fig.14 Heat flux estimated by CGM
总体来看,基于超声传播时间,建立的两种结构内部瞬态温度场重建方法有效,反演的热边界条件符合物理实际,重建的瞬态温度分布精度较高,实时性好,将有利于促进超声无损测温技术的发展。
5 结论
1)本文基于反演稳态、瞬态边界重建的结构内部瞬态温度分布,除个别点外,与真值吻合良好,算法精度高、抗噪性好、稳定性强。
2)比较两种算法,灵敏度法主要适用于稳态边界的反演,推导和实现较为方便,精度和计算效率较好,但是对于瞬态边界反演而言,则受限于信息矩阵的病态特性,效果欠佳,若采用准定常近似,可以有效改善;共轭梯度法能很好地适用于瞬态边界的反演,精度较高,但是推导和实现较为复杂,起点和尾点的反演值需修正。
3)对比文献[19]实验结果可知:基于超声传播时间反演的热边界条件,符合物理实际,重建的瞬态温度分布精度较高,实时性好,适用性强,将有利于促进超声无损测量固体结构内部温度分布技术的发展,具有一定的工程应用价值。
References)
[1] Lu C H, Tsai C C. Adaptive decoupling predictive temperature control for an extrusion barrel in a plastic injection molding process[J]. IEEE Transactions on Industrial Electronics, 2001, 48(5):968-975.
[2] Brown E C, Olley P, Coates P D. In line melt temperature measurement during real time ultrasound monitoring of single screw extrusion[J]. Plastics Rubber & Composites, 1999, 29(1):3-13.
[3] Smith T B, Schetz J A. Development and ground testing of heat flux gages for high enthalpy supersonic flight tests[C]∥22nd Aerodynamic Measurement Technology and Ground Testing Conference. St Louis, Missouri ,US: AIAA, 2002.
[4] Gartenberg E, Roberts A S. Twenty-five years of aerodynamic research with infrared imaging[J]. Journal of Aircraft, 1992, 29(2): 161-171.
[5] Wang H Z, Yu H B, Lin F L. Method and experiment of noninvasive temperature estimation by ultrasound echo pulses[C]∥Proceedings of the 20th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Hong Kong, China: IEEE,1998: 1513-1516.
[6] Koo K M, Jeong D G, Chio J H , et al. A new measurement system of very high temperature in atomic pile using ultrasonic delay time[C]∥IEEE Region 10 International Conference on Electrical and Electronic Technology. Singapore: IEEE,2001.
[7] 孙崇正. 超声波测温技术进展[J]. 宇航计测技术, 1995, 15(2):34-41. SUN Chong-zheng. Progress of ultrasonic thermometry[J]. Astronautic Metrology and Measurement, 1995, 15(2):34-41. (in Chinese)
[8] 常蕾,赵俭. 超声波测温技术在高温气流温度场测量中的应用[J]. 计测技术,2014, 34(1):1-9. CHANG Lei, ZHAO Jian. Application of ultrasonic thermometry in measuring temperature field of high temperature gas flow[J]. Metrology & Measurement Technology, 2014, 34(1):1-9.(in Chinese)
[9] 魏培君, 章梓茂. 弹性动力学反问题的数值反演方法[J]. 力学进展, 2001,31(2):172-180. WEi Pei-jun, ZHANG Zi-mao. Numerical methods for inverse problems in elastic dynamic[J]. Advances in Mechanics, 2001,31(2):172-180.(in Chinese)
[10] Beck J V. Nonlinear estimation applied to the nonlinear inverse heat conduction problem[J]. International Journal of Heat and Mass Transfer, 1970, 13(4):703-716.
[11] Ihara I, Takahashi M. Ultrasound thermometry for monitoring internal temperature gradient in heated material[C]∥IEEE International Ultrasonic Symposium. Rome: IEEE, 2009:1199-1202.
[12] Ihara I, Takahashi M. A new method for internal temperature profile measurement by ultrasound[C]∥Instrumentation and Measurement Technology Conference. Warsaw, Poland: IEEE, 2007.
[13] 钱炜祺, 蔡金狮. 再入航天飞机表面热流密度辨识[J]. 宇航学报, 2000, 21(4): 1-6. QIAN Wei-qi, CAI Jin-shi. Surface heat flux identification of reentry space shuttle[J]. Journal of Astronautics, 2000, 21(4): 1-6.(in Chinese)
[14] 蔡金狮, 汪清, 王文正. 飞行器系统辨识学[M]. 北京:国防工业出版社, 2003. CAI Jin-shi, WANG Qing, WANG Wen-zheng. The aircraft system identification[M]. Beijing: National Defense Industry Press, 2003.(in Chinese)
[15] 钱炜祺, 何开锋, 汪清. 三维非稳态热传导逆问题反演算法研究[J]. 力学学报, 2008, 40(5):611-618. QIAN Wei-qi, HE Kai-feng, WANG Qing. Inverse estimation of heat source term in three dimensional transient heat conduction problems [J]. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40(5):611-618.(in Chinese)
[16] Shi Y A, Zeng L, Qian, W Q, et al. A data processing method in the experiment of heat flux testing using inverse methods[J]. Aerospace Science and Technology, 2013, 29(1): 74-80.
[17] 解可新, 韩健, 林友联. 最优化方法[M]. 天津: 天津大学出版社, 1997. XIE Ke-xin, HAN Jian, LIN You-lian. The optimization methods[M]. Tianjin: Tianjin University Press,1993.(in Chinese)
[18] Alifanov O M. Inverse heat transfer problems[M]. Berlin: Springer-Verlag, 1994.
[19] Takahashi M, Ihara I. Ultrasonic sensing of internal temperature distributions in heated materials[C]∥ International Joint Conference. Busan, Korea: SICE-ICASE,2006:1071-1074.
Reconstruction of Transient Nonuniform Temperature Field in Solid Structures Using Inverse Methods
SHI You-an1,2, WEI Dong2, GUI Ye-wei2, QIAN Wei-qi2, ZENG Lei2, LIU Xiao2
(1.State Key Laboratory of Aerodynamics,China Aerodynamics Research and Development Center, Mianyang 621000, Sichuan, China;2.Computational Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000,Sichuan,China)
A new method is presented for reconstruction of internal transient nonuniform temperature field in solid structures . The proposed method consists of a joint of heat conduction calculation and an inverse analysis for boundary parameter estimation using ultrasonic time of flight by conjugate gradient method or sensitivity method. The principle for internal temperature sensing is based on temperature dependence of the velocity of ultrasonic wave that propagates through solid material. Serial simulation and stability analysis are made, in which classic function form of heat flux or constant temperature is estimated to illustrate the calculating accuracy and the factors of influencing two parameter estimation methods. Comparison experiments with a steel plate which single side is heated by hot water are referred. The temperature gradient and its variation estimated by the two methods agree well with the data measured using thermocouples installed in a steel structure. The results show that the proposed method is a promising means for high accurate reconstruction of internal transient temperature field in solid structure.
ordnance science and technology; transient temperature field; ultrasound speed measurement of temperature; reconstruction of temperature field; sensitivity method; conjugate gradient method
2016-03-17
国家自然科学基金项目(11402285、11372338); 国家“973”计划项目(2015CB755800)
石友安(1985—),男,助理研究员。E-mail:youanshi@sina.com
TB942
A
1000-1093(2016)12-2347-09
10.3969/j.issn.1000-1093.2016.12.022
