将“学思结合”融入初中数学教学
2017-01-06江苏省仪征市第四中学李孝兵
江苏省仪征市第四中学 李孝兵
将“学思结合”融入初中数学教学
江苏省仪征市第四中学 李孝兵
古语有云“学而不思则罔,思而不学则殆”,学习与思考相结合的教学模式被大家称为学思习行,这种学习模式的主要目的就是在教学过程中全面优化教学方式,将学生的各个方面的素质都全面的提升起来。在初中数学的教育过程中,这种学与思互相结合的模式有助于学生更好地理解数学知识。“学”只是一个知识的输入过程,学生通过课本的阅读、教师的讲解获得了新知识,但是所学习的知识很快就会被遗忘,这时“思”就起到了一个非常重要的作用,思考引导学生对知识进行深化和理解。本文就如何将学思结合融入初中数学的课堂,给出了以下几点建议。
一、巧设情境法,将学生作为主体
初中阶段的学生正处于青春期,自我控制能力还达不到一定的高度,如果教师在课堂的教学中墨守成规,严肃认真地向学生们讲课,那么很多同学就无法在课堂上专注听课了,因为课堂枯燥而乏味。因此教师要根据不同年龄段的学生,制定不同的教学方法,其中建立情境法就是有效的教学方式,情境的建立往往是贴近学生的日常生活的,因此很容易就吸引了学生的兴趣。比如在进行《有理数加法》的教学中,教师就可以构建一个生活中的情境帮助学生们理解。比如:星期天的早上,小明的妈妈让小明去超市买一瓶酱油回来,给了小明十块钱,一瓶酱油是六块钱,这时小明就剩余了四元钱。这是学生们在生活中也经常遇见的情况,教师向学生提出疑问:那么小明的钱用有理数的加法该如何表达呢?并将全班学生分为几个小组进行讨论,经过几分钟激烈的讨论,很多小组都探讨出如何用有理数来表达小明所剩余的钱了,就是10+(-6)=4。
这个构建情境的过程不仅让同学们能够更好地理解有理数的加法,而且还将学与思有机结合在一起了,教师在课堂上教授给学生知识后,再向学生提出相关的问题,引发学生思考,对这个知识点有了自己的理解,进一步加深了印象。为什么要思考?原因在于如果某个公式学生忘记了,没关系,只要学生之前很好的进行了思考,理解了这个公式的由来,那么就算忘记了公式,学生还可以顺着思路一步步地推导出正确的公式来,但是如果当时学生在学习这个公式时就是死记硬背下来的,那么忘记了就推导不出来这个公式了。因此思考是学习中不可缺少的一部分。
二、举一反三法,提高学习效率
培养学生的思维能力是学与思结合中一个重要的部分,尤其是在初中数学这门课程中,学习的目的绝对不仅仅是为了解决试卷上的几道题,而是学习数学中的思维方法,并且在日积月累中总结出自己的一套思维模式。初中数学的课堂不应该是静悄悄的,而应该是抒发自己观点的场所,因此课堂讨论是必不可少的,在讨论的过程中进行思维交流,才能学习到更多有用的东西。例如在讲解《轴对称》这一节内容时,教师利用多媒体向学生展示中国古代建筑的图片,让学生们观看,并列举出其中一些关于轴对称的例子,接下来就交给学生讨论,以小组为单位讨论:生活中有哪些地方是轴对称的?在热烈的讨论中,学生的思维活跃程度大幅提高,每个人都积极地思考生活中哪些地方是有轴对称的,当讨论结束后,由教师总结出大家的答案,如果有不是轴对称的图形,要及时改正学生出现的这个问题。
这种小组学习的模式不止在课堂讨论中可以运用,在课下也可以使用这种合作学习的方法。每个学生都有自己的长处和短处,在小组合作学习的过程中可以取长补短,拓宽思维的广度。举一个例子,在教授“圆与圆的位置关系”这一知识点时,由于较为抽象,学生很难及时反应过来,这时教师为了化抽象为具体,给每一个学习小组都发放两张一模一样的圆形纸,在接下来的讲解中,让学生们比对着手中的图纸进行学习和思考,教师也可以在教学前让学生们自己思考圆与圆的位置关系应该有几种,并分组讨论。这都是学习和思考融会贯通的方法。
三、勤学多练法,统一学与思
学习与思考的融合是少不了做题的,从题目中思考解题方式或是反思这道题为什么做错了,都是初中数学课堂中必不可少的一部分,在实际题目中,把所学习的知识变成解题最重要的思想路线,这是最基本也是最有效的一种办法。想要将新学习到的种种知识变成学生自己的所有物,首先第一步就是多做题练习。题目是千变万化的,但是知识点是不会改变的,当学生十分熟悉了某一知识点,就会发现那些变来变去的题目所涉及的知识点无非就那两三个,以后再遇到这种题目时,就不用担心不会做这件事了。比如这道题:如图所示,三角形ABC中,AD为中线,P为AD上任意一点,过P的直线交AB于M,交AC于N,若AN=AM,求证PM/PN=AC/AB。
证明:如图所示,过P点作BC的平行线交AB,AC分别于点M′,N′;再分别过M,M′两点分别作AC的平行线分别交AD(或延长线)于P′,A′两点。
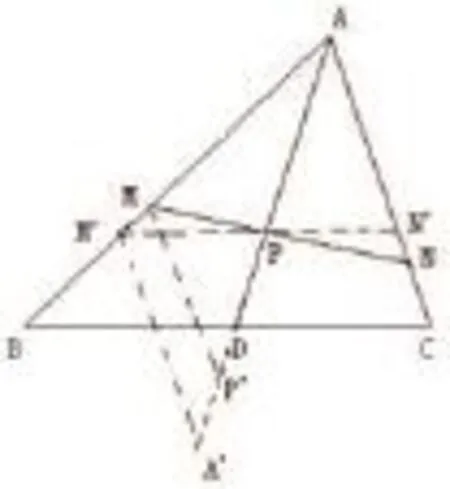
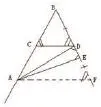
由M′N′∥BC得:AC/AN′=AB/AM′,即AC/AB=AN′/AM′,且M′P=N′P。
由三角形AN′P全等于三角形A′M′P得:M′A′=AN′。所以AC/AB=A′M′/AM′。
由三角形AM′A′相似于三角形AMP′得:AM/AM′=MP′/A′M′,即A′M′/AM′=MP′/AM。
所以AC/AB=MP′/AM。
由三角形MP′P相似于三角形ANP得:MP′/AN=MP/PN。
而AN=AM,
所以MP/PN=AC/AB。
在这道题中,学生看到题目就要思考:这道题中运用了哪几个知识点,在平时的课堂中教师一定也讲过不少类似的题目,慢慢整理思路,一步一步地写出解题步骤,如果这道题做错了,也要及时反思哪里出现了问题,及时整改,才能在以后的学习中更加轻松。
综上所述,将学与思结合在一起可以有很多的方法,数学本就是一个严谨的科目,教师在进行教学时要注重知识和方法的双重教授,学思结合,知行合一,才能更好地提高学生的学习能力。
