反比例函数最值问题解题方法分析
2017-01-06江苏省南京市玄武外国语学校
江苏省南京市玄武外国语学校 沈 艳
反比例函数最值问题解题方法分析
江苏省南京市玄武外国语学校 沈 艳
反比例函数的最值问题由于其强大的兼容性,可以结合多种函数知识,能更好地考查学生综合运用数学知识的能力以及对数学思想方法的掌握情况,成为了近年来中考的热门题型。本文针对不同的最值情况提出不同的解题方法,以供学生复习参考。
最值问题;反比例函数;综合应用
本文从线段最值,周长最值,面积最值三个角度依次举例说明与反比例函数相关的最值问题的解法,数形结合思想、方程思想等数学思想在此过程中有着重要的应用。
一、三角形性质法
巧妙构造三角形,利用三角形中两边之和大于第三边以及两边之差小于第三边的性质,可以判断出线段和或差的最值问题。
解析:先利用点的坐标求出函数中的未知量,再结合三角形各边的关系找出最小值。将A点坐标分别代入y1、y2求得k=-2/3,m=-12。

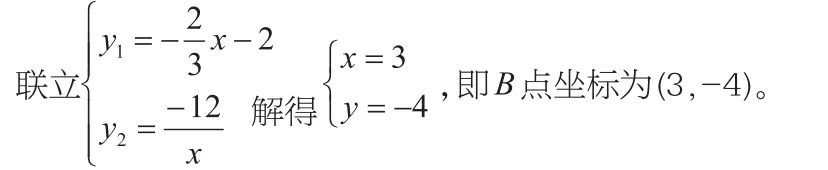
当PA,PB与AB构成一个三角形时,由三角形三边关系可知|PA+PB|>|AB|恒成立,故当且仅当P在AB上时,|PA+PB|最小,且等于。
点拨:本题中通过三角形解题,不需要分别列式计算PA、PB的长,使问题由繁化简,节省了很大的计算量,是数形结合思想的完美体现。
二、配方法
配方法就是将关系式配成二次函数或者三次函数的形式,再利用相关知识解答,在解题时出现不在课本上介绍过的初等函数范围内时,常用配方法解决。

OABC的周长,然后利用配方法求最小值。
AC=m,AB=,因为AB⊥x轴和AC⊥y轴,OC⊥OB,所以四边形OBAC为矩形,故其周长为:
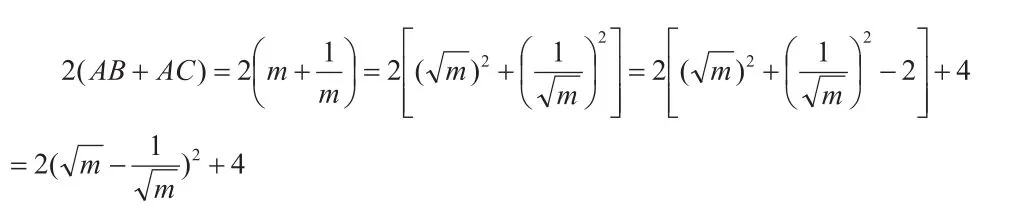
点拨:本题用四边形周长代数式的特点列出的函数式是中学阶段较为常见的也是很重要的关系式,利用配方法解此式是学生应该掌握的解题能力。
三、二次函数法
将数量关系表达为二次函数,根据其函数性质就可以很直接地看出最值的有无以及大小了,此法多见于求多边形周长或者面积的最值问题。下面例题中为面积最值。

解析:将点B的坐标代入,解得c=-5,则,将点的坐标代入y2,得d=-2,则,而一次函数y1=kx+b的图象经过B(-1,5)、两点,故。令y1=0,解得x=3/2,故,由题意,设,因为DP∥x轴,且点D在y2的图象上,故,即。则△PAD的面积为。又n=-2m+3, -1<m<3/2,得0<n<5,而,故当时,即时,△PAD的面积S最大,为。
点拨:本题在反比例函数的知识点上又综合考査了一次函数的解法、二次函数的解法等初中的核心内容,在能力上检验了学生在动态情形下对图形的观察分析能力及函数知识的综合应用能力。
从本文的举例中可以看出,反比例函数最值问题应用的数学方法多,纵横联系复杂,注重数学思想的运用,希望在提升学生解此类问题能力的同时可以激发学生的探索兴趣,塑造自身的思维品质。
