农作物品种最佳聚类方法研究

杜海平

（山西省农业科学院农业科技信息研究所，山西太原030031）

农作物品种最佳聚类方法研究

杜海平

（山西省农业科学院农业科技信息研究所，山西太原030031）

筛选中国知网上的期刊文献，选择4篇文章中的4种豆类数据作为评判标准，对数据变换7种方法、样品间5种距离公式、类间7种距离定义，共组合成的245种分类方法，应用系统聚类分析、方差分析、非参数检验和描述性统计分析等方法进行了比较研究。结果表明，过去最常使用的类间最短距离法和类平均距离法都不是最佳的类间距离方法，它们的准确性极显著地低于最小离差平方和法；原始数据Z标准化变换也不是最佳的变换方法,而是“全距从0到1”、“全距从-1到1”、“1的最大量”这3种变换方法；样品间5种距离分类最准确的是Manhattan距离，其次才是欧氏距离。据此得出了最佳的聚类方法和步骤。

农作物品种；聚类方法；数据变换；类间距离；样品间距离

聚类分析是根据事物的多个数值特征来观察事物个体之间或样品之间的亲疏关系和相似程度的一种多元统计分析方法，内容涉及面广，分类方法多而杂[1-3]，其理论上还不是至善至美，但是它比凭感官分类效果要好、分类结果明确，借助计算机和统计软件，分类速度很快。

在农业和生物学研究中，聚类分析有着广泛的应用，比如品种分类、生产性状分类、表型性状分类、土壤分类等。经过分类，可以发现每类的特征，再通过特定试验，从而可以应用方差分析、相关分析、回归分析等进一步揭示类群间的关系。

聚类分析是根据样品之间的亲疏关系进行分类，亲疏关系是根据样品与样品之间、类与类之间的距离远近来衡量的，而距离远近又与多种距离公式和聚类方法的选择有关。

从应用的角度，申慧芳等[4-6]使用最短距离法，李莉等[7-9]使用最长距离法，要燕杰等[10-12]使用类间平均法，赵明辉等[13-15]使用离差平方和法，孙敏等[16]使用质心聚类法。从理论的角度，陈庆富等[17-18]推崇最短距离法，向晓群[19]持相反态度；张文彤等[20-21]认为，类平均距离法表现最为优异，克劳斯·巴克豪斯等[22]却认为Ward法最好，而盖钧镒[23]认为最小组内平方和法和组平均法效果都较好。因此，产生了折中办法，李静萍等[24-25]建议，尽量多用几种距离公式和分类方法进行聚类分析，从多种结果中找出合适的分类，于是对同样一批样品进行分类，由于多种选择，就会得到多种分类结果。这就造成了许多科技人员在使用聚类分析方法时的疑惑和困难，计算量、工作量大增，而分类结果却未尽合理。

为了对多种距离公式、聚类方法及数据转换方法的不同组合进行比较，探索最佳的聚类分析方法，本研究仅从农业科研试验数据的角度出发，选用4种豆类品种作为评判比较标准，经过数千次的计算、分析、验证，寻找基于SPSS软件当中系统聚类方法下所有组合的最优聚类搭配，以期给农业科技人员在对农作物品种应用聚类分析时提供理论依据和实际操作方法。

1 材料和方法

1.1 数据来源

4组豆类数据，即绿豆、红小豆、豌豆、大豆，分别来源于文献[4-5，7，26]。

1.2 数据选取方法

从品种上考虑，第1，2组采用文献[4-5]中的全部品种；第3组只取用文献[7]中的10个品种，剔除5个极端值品种；第4组取用文献[26]中的第1个试验点品种，剔除第2个点的品种。

从性状上考虑，选取4组豆类共有性状的数据，它们是“株高、分枝数、主茎节数、单株荚数、单荚粒数、百粒质量、生育期、单株产量”。

另外，根据公式“单株粒数＝单株产量/（百粒质量/100），单荚粒数＝单株粒数/单株荚数”，计算补充了第3组中“单荚粒数”的数据缺失。

除8个生物学性状变量外，再增加一个变量“豆类”，相当于方差分析中的处理，它有4个水平，分别是绿豆、红小豆、豌豆和大豆。这样，这组数据共有9个变量45个品种。其中，绿豆12个品种，红小豆13个品种，豌豆10个品种，大豆10个品种（表1）。

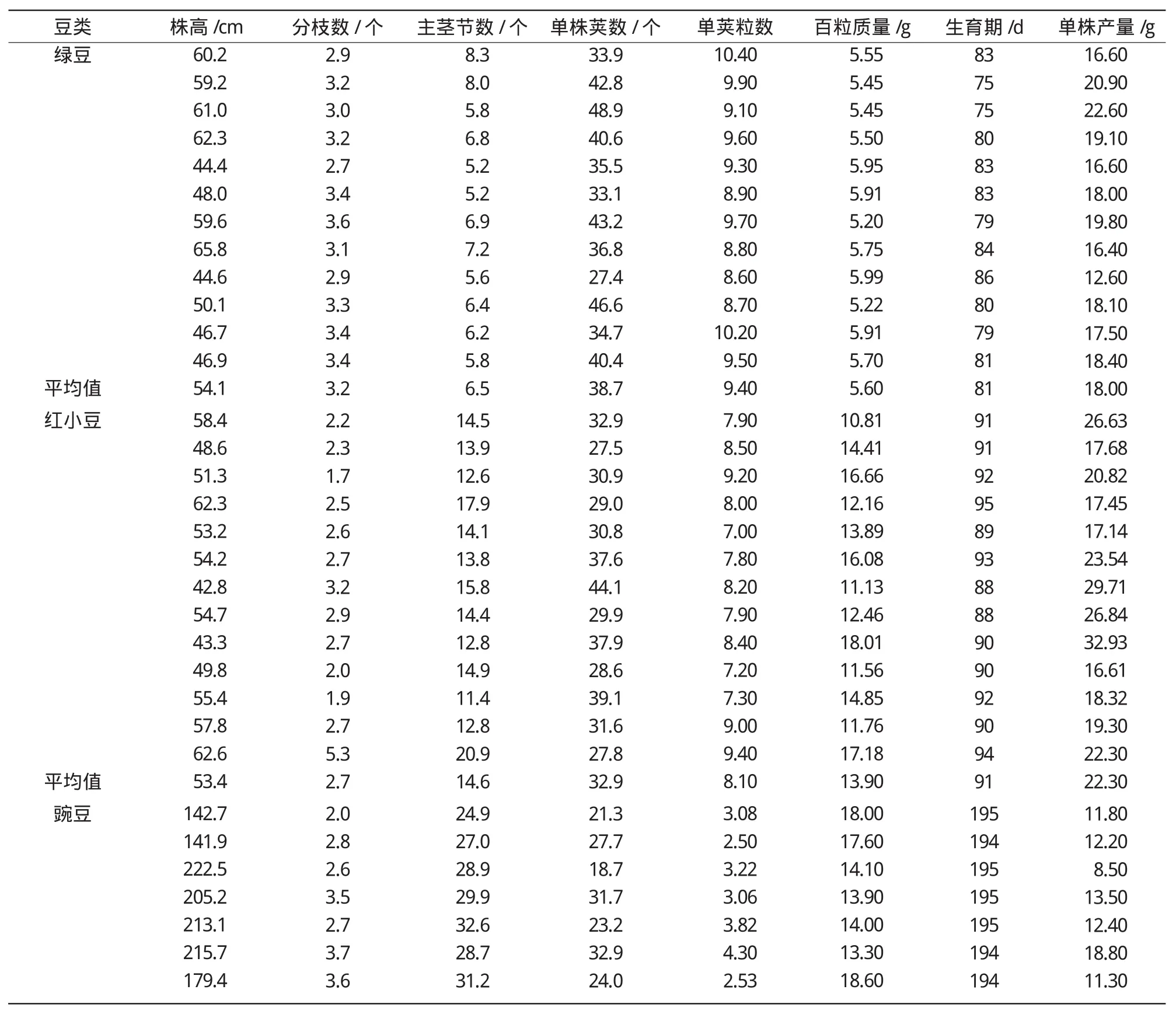
表1 原始数据

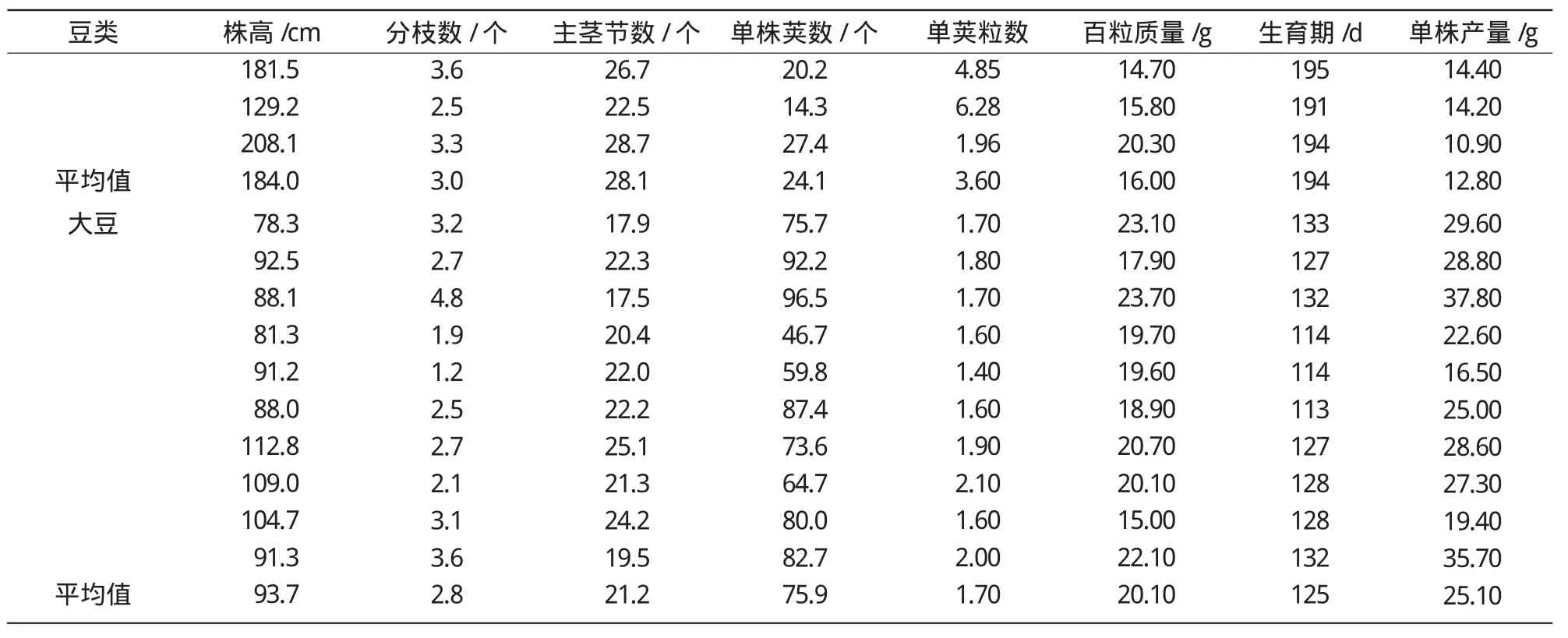
续表1

1.3 研究方法

本研究基于SPSS统计软件，采用系统聚类方法，对样品间5种距离公式、类间7种距离公式、数据变换7种方法这三者之间245个组合都进行一次聚类分析，要求把所选样品分为四类，以此聚类结果与标准的四类范本进行比较，统计出分错类样品的数目，再应用统计手段进行分析，从而得出不同聚类组合之间的优劣。本研究中“样品”等同于品种，只是它适用范围更广。

1.4 距离公式定义及数据变换方法

假设有n个样品Xi，对每个样品Xi观测了m个指标或性状，即Xi＝[xi1xi2… xim]，其中xik为第i个样品的第k个指标的观测值。这样，得到原始观测数据阵如下。

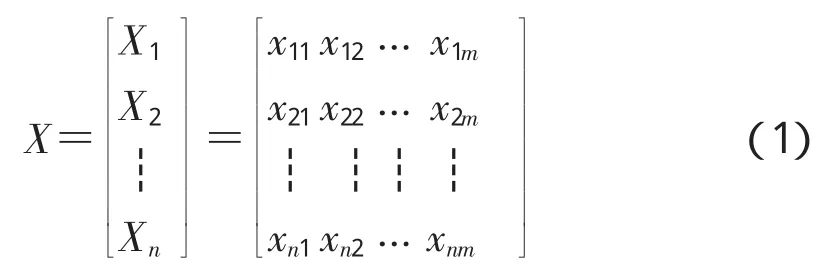
设第i个样品Xi与第j个样品Xj之间的距离用dij表示，即dij＝d（Xi，Xj）。

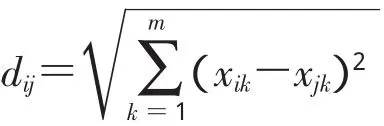
从以上各公式可以看出，各指标或性状的单位要相同才能进行运算，才有实际意义，否则需要先对各指标进行标准化变换后才能使用这些公式。

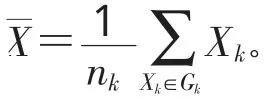
类间平均距离（组间联接法），即2类之间两两样品距离之和的平均值。

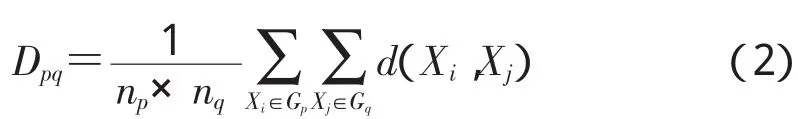
类内平均距离（组内联接法），即两类合并为一类后所有样品两两间距离之和的平均值。

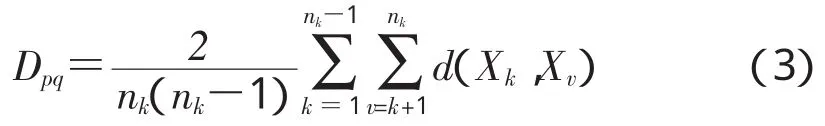
最近邻元素法，即2类之间最近2个样品的距离作为2类之间的距离。

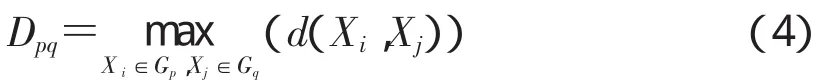
最远邻元素法（完全连接法），即2类间最远的2个样品的距离作为2类之间的距离。

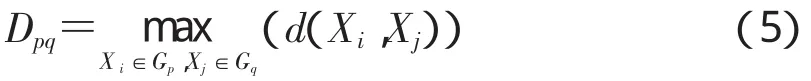
重心聚类法（质心聚类法），即2类中各自样品均值之间的距离作为类间距离。

中间距离法（中位数法或median method）：Gk与任一类Gr的距离公式如下。

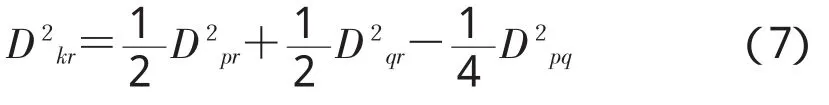
Ward法（离差平方和法），即两类合并后增加的离差平方和作为两类间的距离，选择使离差平方和增加最小的两类合并，直到所有的样品归为一类为止。

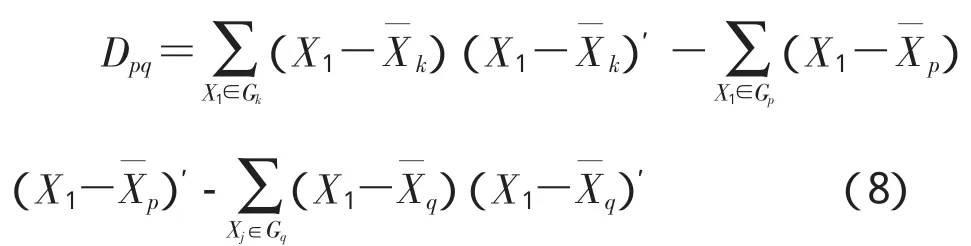
1.4.3 原始数据7种转换方法

1.4.3.1 不转换 不对原始数据进行标准化。

1.4.3.2 Z得分 将原数标准化为均值为0、标准差为1的数值。计算方法为原数减去其变量均值，再除以标准差；如果标准差为0，转换后的值也为0。

1.4.3.3 全距从-1到1 将原数标准化为-1～1的数值。计算方法为原数减去均值，再除以极差；若极差为0，则原值不变。该方法适用有负值情况。

1.4.3.4 全距从0到1 将原数变换为0～1的值。计算方法为原数减去其变量中最小值，再除以极差；若极差为0，则变换后的值设为0.5。

1.4.3.5 1的最大量 将原数标准化为最大不超过1的数值。计算方法为原数除以其变量中最大值；如果最大值为0，则为原数除以其变量中最小值的绝对值，再加1。

1.4.3.6 均值为1 将原数标准化为均值为1的数值。计算方法为原数除以其变量的均值；如果均值为0，则为原数加1。

1.4.3.7 标准差为1 将原数标准化为标准差为1的数值。计算方法为原数除以其变量的标准差；如果标准差为0，则原数值不变。

1.5 系统聚类过程

将n个样本或样品看成n类，计算所有样品两两之间的距离；把最短距离的2个样品聚成一类，于是总类数就减少了一类，变成了n-1类；继续计算样品之间、或样品与类之间、或类与类之间的距离；每次都把距离最短的聚成一类，这样每次减少一类；循环往复，直到最后所有样品聚成了一个大类。

2 结果与分析

2.1 4种豆类间差异显著性分析

从表1中8个指标的平均数可以看出，它们各自在4种豆类之间都有不同程度的差异，但是其差异是否能够达到把4种豆类区分清楚的显著程度，还有必要进行方差分析。

经过检验、数据转换、再检验，数据符合正态性和方差同质性；显然，数据也符合独立性。这样，数据具备了方差分析的3个必要条件，可以进行方差分析。

多变量方差分析显示，4种豆类在8个指标的总体上差异极显著。8个指标各自的单变量方差分析显示，除分枝数不显著外，其他7个指标各自在4种豆类间都差异极显著。对极显著的7个指标分别进行4种豆类间的多重比较，结果表明，绝大多数都显著，只有红小豆与绿豆在株高间、单株荚数间差异不显著。

综上所述，4种豆类除在分枝数上差异不显著、红小豆与绿豆在株高和单株荚数上差异不显著外，其他40个多重比较间都差异显著或极显著，有很好的分类基础，与直观上认为它们容易被区分的判断是一致的。因此，把这4种豆类作为评判众多聚类方法优劣的标准是可行的。

2.2 对原始数据进行分类的结果与分析

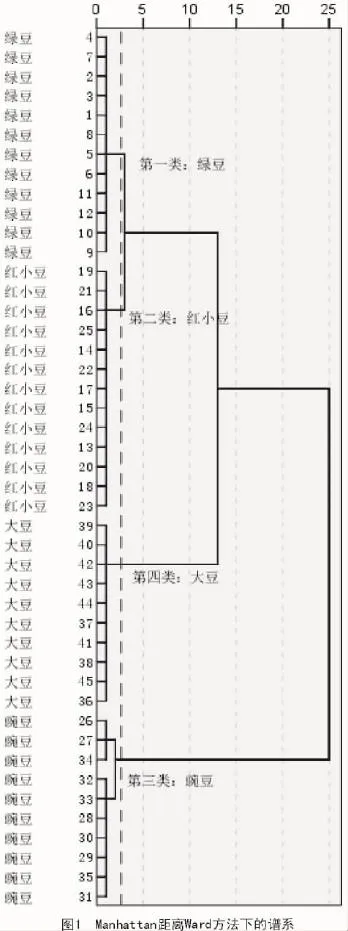
使用样品间距离与类间距离的35种组合方法，分别对原始数据进行聚类分析。结果表明，35种方法中，有34种不能准确把45个品种分成四类，只有Ward法对应Manhattan距离这个组合能够准确分成四类（图1），完全正确率小于3%。在图1中2.6处样品被分成了4类，分别是绿豆、红小豆、大豆和豌豆。

在35次聚类中，分错最多的是最近邻元素法和中间距离法分别对应Chebychev距离这2个组合，它们把绿豆、红小豆和大豆都分到同一类里，而把豌豆拆分为3类，分错数达27个，分错率达60%。

由此可见，如果直接对原始数据进行分类，其分类效果很差，因为各变量单位不统一，数量级别差异也大。所以，要想提高分类的正确率，必须对原始数据进行一定的变换处理。

2.3 7种数据变换（包括原始数据）的分类结果与分析

对7种数据变换、7种类间距离、5种样品间距离，共245种组合方法的聚类结果，汇总其分类样品数，结果如表2所示。

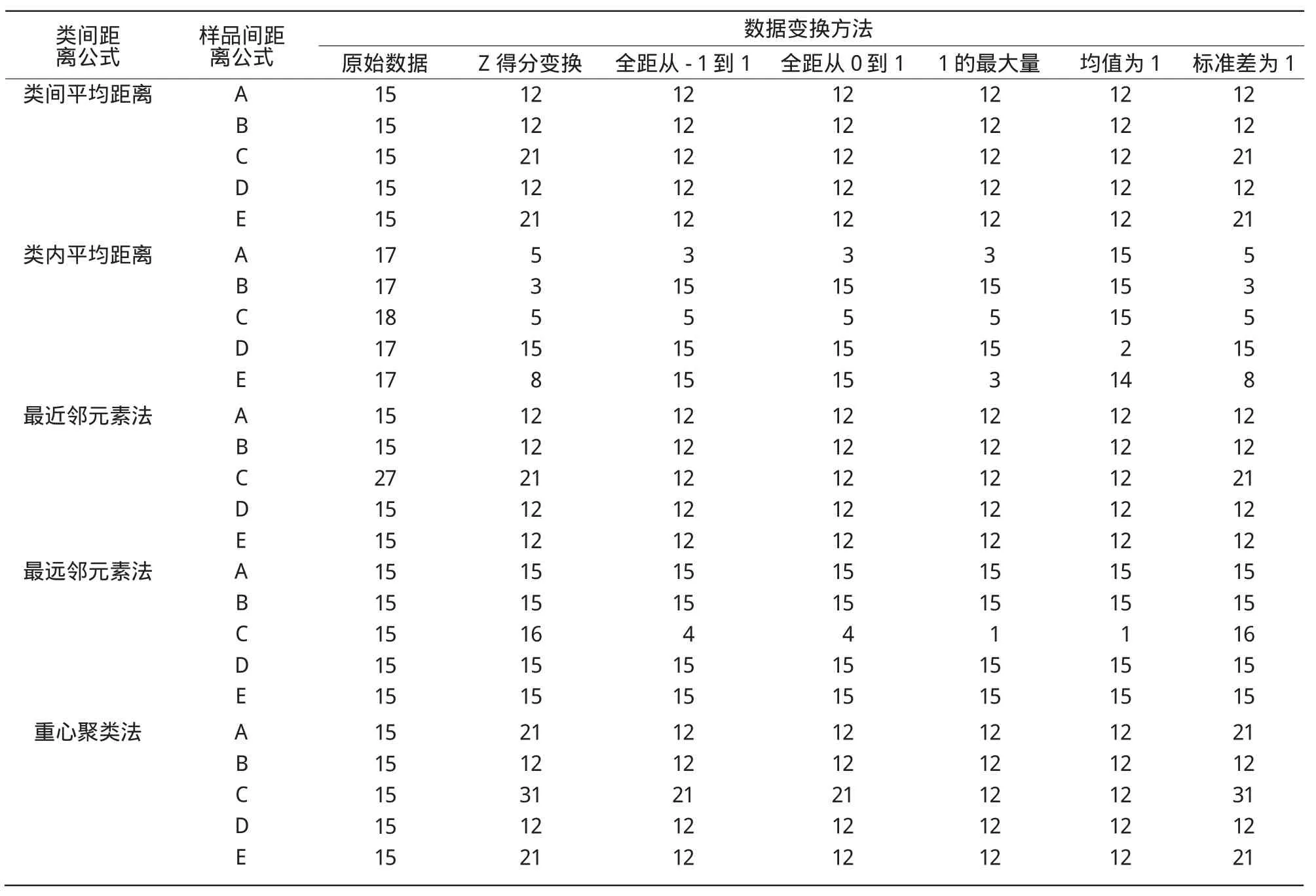
表2 原始数据7种变换下分错样品数汇总

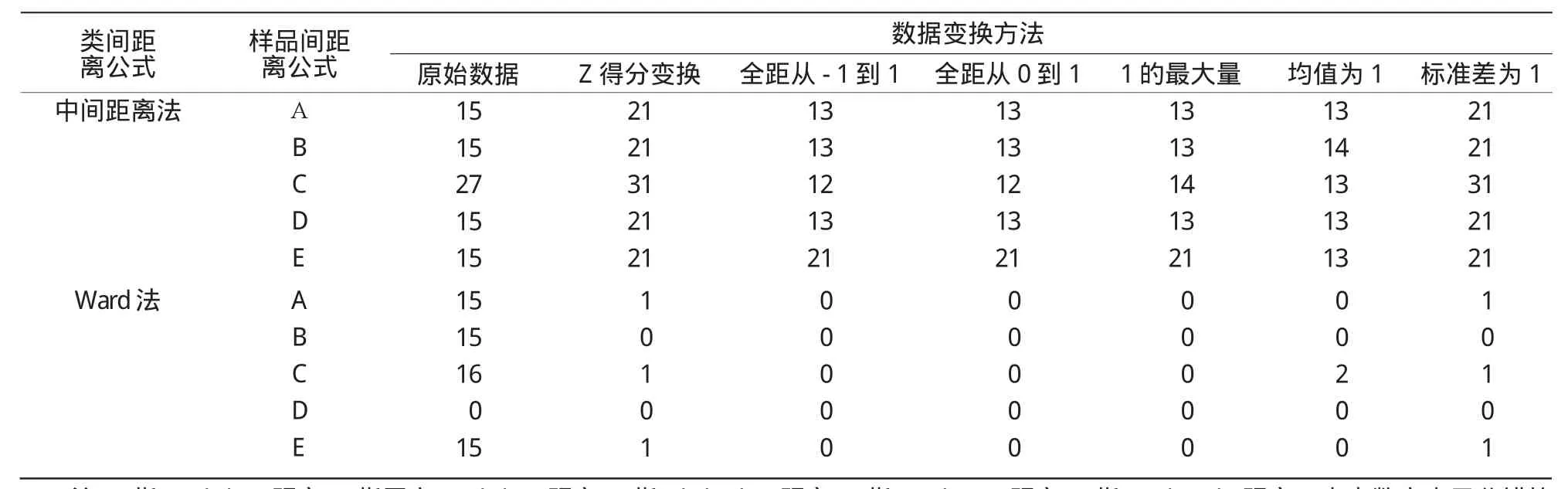
续表2

由表2可知，“原始数据”这一列中，只有Ward法对应的D行为0，表示分类正确。“Z得分变换”一列中，分类效果最好的是Ward法，其次是类内平均距离法。但能够准确分成四类的只有类间距离Ward法对应的B行和D行，即Ward法对应平方Euclidean距离和Manhattan距离的分类效果最好。Ward法对应的另外3行各分错了一个样品；类内平均距离法对应的A行分错了5个，对应的B行分错了3个，对应的C行分错了5个。可见，经过Z标准化变换，分类正确率有明显的提高。

为准确把握各种方法和距离的优劣，本该应用方差分析和多重比较进一步分析，但是通过检验，发现此表数据不满足正态性和方差同质性要求，只能改用非参数检验和描述性统计进行分析。

通过Kruskal Wallis检验，得出类间7种距离之间、数据变换7种方法之间差异极显著，而样品间5种距离之间差异不显著。

经Mann-Whitney检验显示，Ward法分错数极显著低于其他6种方法；数据变换中，“1的最大量”、“均值为1”、“全距从-1到1”、“全距从0到1”都极显著低于原始数据的分错数，但这4个间差异不显著，有必要加入新的品种数据进一步分析。2.4 60个品种的分类结果与分析

把前面分析时剔除的15个品种（1.2中5个豌豆品种和10个大豆品种），也参与了分类。豌豆品种变成15个，大豆品种变成20个，绿豆和红小豆分别还是12，13个品种。对这60个品种进行245次聚类分析，对分错数结果进行独立样本的非参数检验等分析。其部分分析结果如图2～4、表3所示。

由图2～4可知，类间距离、数据变换、样品间距离分错数最少的分别是Ward法、“全距从-1到1”和“全距从0到1”、Manhattan距离，并且通过Mann-Whitney检验，显示它们的分错数都极显著低于别的距离或方法的分错数。

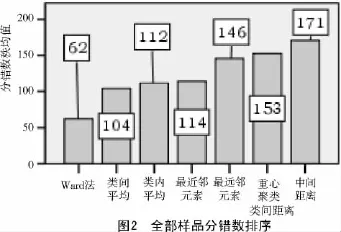
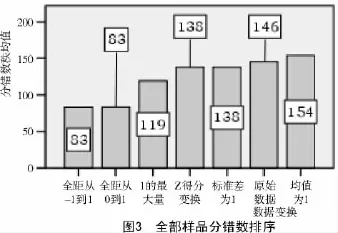
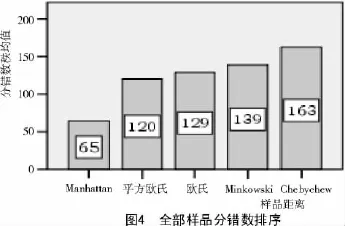
表3 60个品种Ward法变换下分类错误汇总

3 结论与讨论

本研究以4种豆类数据为评判标准，进行了大量的推演和计算，最后得出了比较可靠的品种最佳聚类方法。首先，选择数据变换方法。这一步是为了消除不同指标不同量纲的影响和数量级别落差大的影响。在最常用的7种数据变换方法中，得出最好的方法是“全距从0到1”、“全距从-1到1”、“1的最大量”（因为它们3个在配合使用Ward法和Manhattan距离以及原始数据没有负数时差异不大）。其次，选择类间距离。类间距离显然应该选Ward方法，它的分类准确性远高于其他6种方法。第三，选择样品间距离。最好的样品间距离方法是Manhattan距离，其次是Euclidean距离和Minkowski距离3次方。

为了验证上述最优组合在某一类样品比较少的情况下准确性如何，本研究把表1每一类只留2个品种、而其他三类品种数不变，又针对2.4中60个品种把每一类只留3个品种，而其他三类品种数不变，共8种情况，进行了数千次计算分析，得出了和上面一致的结论。

本研究的缺憾是样本量仍然不是很大，每类样本数没有超过20个，有待以后收集更多的数据进一步检验这种最优组合方法的外延正确率。

［1］Jain A K.Data clustering：50 years beyond k-means[J].Pattern Recognition Letters，2010，31（8）：651-666.

［2］孙吉贵，刘杰，赵连宇.聚类算法研究 [J].软件学报，2008，19（1）：48-61.

［3］王骏，王士同，邓赵红.聚类分析研究中的若干问题[J].控制与决策，2012，27（3）：321-328.

［4］申慧芳，李国柱.不同绿豆突变体主要农艺性状的多元遗传分析[J].激光生物学报，2010，19（2）：194-200.

［5］申慧芳，李国柱.红小豆主要数量性状的主成分与聚类分析[J].山西农业科学，2012，40（4）：310-313，385.

［6］张学余，苏一军，李国辉，等.部分地方鸡种蛋品质与生态环境的聚类和主成分分析[J].天津农业科学，2013，19（1）：47-50.

［7］李莉，万正煌，焦春海，等.外引豌豆资源的鉴定及主要数量性状的主成分分析[J].湖北农业科学，2014，53（23）：5643-5648.

［8］王林海，王晓伟，詹克慧，等.黄淮麦区部分小麦种质资源农艺性状的聚类分析[J].中国农学通报，2008，24（4）：186-191.

［9］马蓉丽，焦彦生，成妍，等.基于表型性状的辣椒资源遗传多样性分析[J].山西农业科学，2015，43（12）：1577-1581.

［10］要燕杰，高翔，吴丹，等.小麦农艺性状与品质特性的多元分析与评价[J].植物遗传资源学报，2014，15（1）：38-47.

［11］王成，闫峰，崔秀辉，等.绿豆农艺性状的遗传多样性分析[J].杂粮作物，2010，30（3）：182-184.

［12］叶伟庆，王光琴，杨芬霞，等.信宜怀乡鸡体质量与体尺性状的相关性及聚类分析[J].河南农业科学，2015，44（2）：132-134.

［13］赵明辉，李会敏，孟祥海，等.斯洛伐克104份冬小麦种质资源农艺性状的分析及评价 [J].华北农学报，2014，29（增刊）：120-124.

［14］史凤玉，朱英波，龙茹，等.野生大豆抗大豆花叶病毒病评价、聚类及性状间相关分析[J].大豆科学，2010，29（6）：976-981.

［15］孙振纲，姜艳丽，陈耕，等.27个陆地棉新种质材料主要性状研究及聚类分析[J].山西农业科学，2015，43（7）：773-776.

［16］孙敏，黎娟，周清明，等.湖南浓香型烟叶不同类型区化学成分比较[J].天津农业科学，2016，22（5）：58-62，66.

［17］陈庆富.生物统计学 [M].北京：高等教育出版社，2011：225，238.

［18］方开泰.实用多元统计分析[M].上海：华东师范大学出版社，1992：241.

［19］何晓群.多元统计分析[M].2版.北京：中国人民大学出版社，2009：73.

［20］张文彤，董伟.SPSS统计分析高级教程[M].2版.北京：高等教育出版社，2013：298.

［21］李卫东.应用多元统计分析[M].北京：北京大学出版社，2008：129.

［22］克劳斯·巴克豪斯，本德·埃里克森，伍尔夫·普林克，等.多元统计分析方法[M].上海：世纪出版集团格致出版社，上海人民出版社，2009：328.

［23］盖钧镒.试验统计方法[M].4版.北京：中国农业出版社，2013：215.

［24］李静萍.多元统计分析[M].北京：中国人民大学出版社，2015：49，65.

［25］顾志峰，叶乃好，石耀华.实用生物统计学[M].北京：科学出版社，2012：245.

［26］张玉革，胡绪彬.基于主成分和聚类分析的大豆品种生物学性状的比较研究[J].大豆科学，2004，23（3）：178-183.

Study on the Best Clustering M ethod of Crop Varieties

DU Haiping
（InstituteofAgricultural Information，Shanxi Academy ofAgricultural Sciences，Taiyuan 030031，China）

Screening CNKI journal literature,four kinds of legume data from four articles were used as evaluation criteria.245 clustering methods consisting of 7 methods of data transformation,5 distance formulas between samples,7 distance definitions between classes were compared by cluster analysis,ANOVA,nonparametric test and descriptive statistical analysis.The results showed that, nearest neighbor and between-groups linkage used most commonly in the past were not the best clustering method,because their accuracy was significantly lower than Ward's method.Z standardization was not the best method of data transformation,but it was the "Range from 0 to 1","Range from-1 to 1"and"Maximum Magnitude of 1"3 kinds of transformation methods.Among the 5 distance formulasbetween samples,themostaccurate classification was the Manhattan distance,followed by the Euclidean distance.Accordingly, we got the bestclusteringmethodsand steps.

crop varieties;clusteringmethod;data transformation;between-classdistance;distance between samples

TP399

A

1002-2481（2016）07-0918-07

10.3969/j.issn.1002-2481.2016.07.07

2016-03-21

山西省农业科学院科技攻关项目（2012ygg30）

杜海平（1962-），男，山西太原人，助理研究员，主要从事试验统计分析和大数据应用研究工作。