基于改进加权灰色GM(1,1)模型的高速公路交通量预测

潘 勇，吴小丽，李 科

(招商局重庆交通科研设计院有限公司， 重庆 400067)

基于改进加权灰色GM(1,1)模型的高速公路交通量预测

潘 勇，吴小丽，李 科

(招商局重庆交通科研设计院有限公司， 重庆 400067)

针对具有跳跃性的中长时数据预测，提出一种改进加权灰色GM(1，1)模型对高速公路收费站交通量进行预测。将原始交通量数据经过1阶弱化和1-AGO处理后，利用灰色关联度对初始值的取值进行加权优化，同时对背景值采取光滑优化处理，从而组合成新型灰色GM(1，1)模型。应用某收费站实际交通量统计数据来验证新型灰色GM(1，1)模型算法预测准确性，结果表明：改进加权灰色GM(1,1)模型具有更好的适用性和准确性。

改进灰色GM(1,1)模型；交通量预测；加权

交通量预测一直都是智能交通的核心问题之一，对交通规划设计具有决定性的作用[1]。随着国内交通运输业的快速发展，交通量预测的理论和方法也不断创新。现阶段，学者们提出了多种模型预测交通量，如神经网络模型、马尔科夫链模型、数据挖掘模型[2-4]等。目前，基于灰色模型的交通量预测方法的研究多是对短时数据或贫瘠数据的分析预测；而涉及中长时数据时，由于数据序列跳跃性增长较大，原有模型存在不同程度的局限性和不准确性[5-7]。

文献[7]提出一种对背景值的优化方法，该方法成功提高了灰色模型的预测精度。借鉴该文献对背景值的优化，改进加权灰色GM(1,1)模型又利用灰色关联度对初始值进行加权优化，以改善中长时原始离散数据和背景值的光滑度，提高初始值的准确性。本文应用某收费站实际交通量统计数据来验证改进加权灰色GM(1,1)模型，首次提出用小段数据加权计算总数据间的关联度。对比试验表明，改进加权灰色GM(1,1)模型在精度和适用性上更为优越。

1 改进加权灰色GM(1,1)模型

1.1 灰色GM(1,1)模型原理

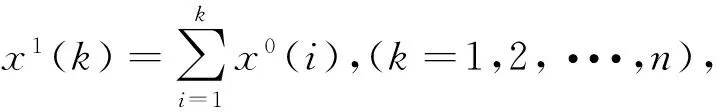
x0(k)+ax1(k)=b

(1)

为灰色模型的最初形式。式中：a为发展系数；b为灰作用量。

定义2：设X0、X1如定义1所示，Z1为X1的紧邻均值生成序列Z1=(z1(1),z1(2),···,z1(n))，其中Z1为背景值，且Z1(k)=θx1(k)+(1-θ)x1(k-1),k=2,···,n，一般取θ值为0.5，则

x0(k)+az1(k)=b

(2)

为GM(1，1)模型的基本形式。

若φ=[a,b]T为参数列，且设参数B、Y为：

则灰色模型x0(k)+az1(k)=b的最小二乘法参数列满足

(3)

根据初始状态x1(1)=x0(1)，可得

(4)

进行1-AGO的逆操作，可得

(5)

1.2 灰色关联度

目前已有各种灰色关联度计算方法。邓聚龙最初给出的关联度是根据时间曲线和几何图形的相识程度来判断关联程度[8]。考虑到邓氏关联度应用的局限和关联度不足等缺陷[9]，文献[9]提出按照因素的时间序列曲线变化形态来计算灰色关联度。本文通过改进的灰色关联度来加权优化初始值。

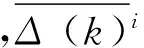
xi(k-1))

(6)

设序列X0与Xi的灰色关联度为：

(7)

式中：i=0,1,2,…,m;k=0,1,2,…,n。

1.3 改进加权灰色GM(1,1)模型

由灰色GM(1,1)模型的建立可知，最初形式的灰色模型由于直接进行1-AGO运算，故预测模型准确度都取决于给定的非负序列、基于原始序列和1-AGO序列构造的背景值Z1以及构造参数a和b。

目前有很多学者对该原始模型进行了改进。本文根据文献[7]在[k,k+ 1]区间内积分的方法，对原始离散数据进行对数变换处理，以提高数列的光滑度。令

(8)

式中：k=2,3,…n。

很多文献中已经提到了最初状态的初始值x1(1)=x0(1)是不准确的[10-11]。在文献[11]中，研究者认为最后一个数据是目前最接近实际情况的。根据改进的灰色关联度加权参数，以前已经有学者提出利用类似的方法对系数a和b中的Y值进行加权优化[12]，本文提出最初状态值的关联度加权初始值，并融合公式(8)中对背景值进行积分优化处理，构建一个改进加权灰色GM(1,1)模型。由于2种优化是完全独立的参数优化，故理论上新的灰色预测模型准确值更高。

假设X0为单调增长的序列，根据公式(7)，序列X0和X1的关联度值为：

(9)

关联度基数为：

Ri=γ01+γ02+…+γ0n

(10)

初始值加权模型为：

(11)

2 应用分析

统计某收费站历年来单月车辆实际通行量，如表1所示。表1中，交通量数据已经按照《道路通行能力手册》标准换算为当量交通量。

表1 某收费站2007—2011年单月车辆通行量

在用灰色模型进行预测前，先对原始数据进行初步检测。

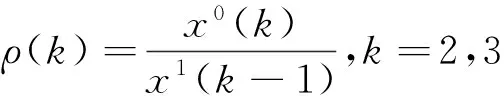
(12)

式中：k=1,2,…n。

对原始数据进行准光滑检验并对准指数规律进行检验，得

ρ(k)=[1.9,0.98,0.58,0.66]

对原始数据进行1阶弱化处理，可得

x0(k)=[353 305.6,411 366,465 208.3,547 648.5,704 832]

2.1 原灰色GM(1,1)模型预测

根据公式(3)，可得

a=0.183

b=2.96×105

2.2 改进加权灰色GM(1,1)模型预测

根据公式(2)、(3)和(8)，对模型背景值进行计算，可得

Z1(k)=[532 779.5,983 638.2,1 498 057.5,2 121 465.9]

其中：a=0.182,b=3.01×105。

验证只优化背景值的改进灰色模型的预测值为：

其中：x0(1)=353 305.6。

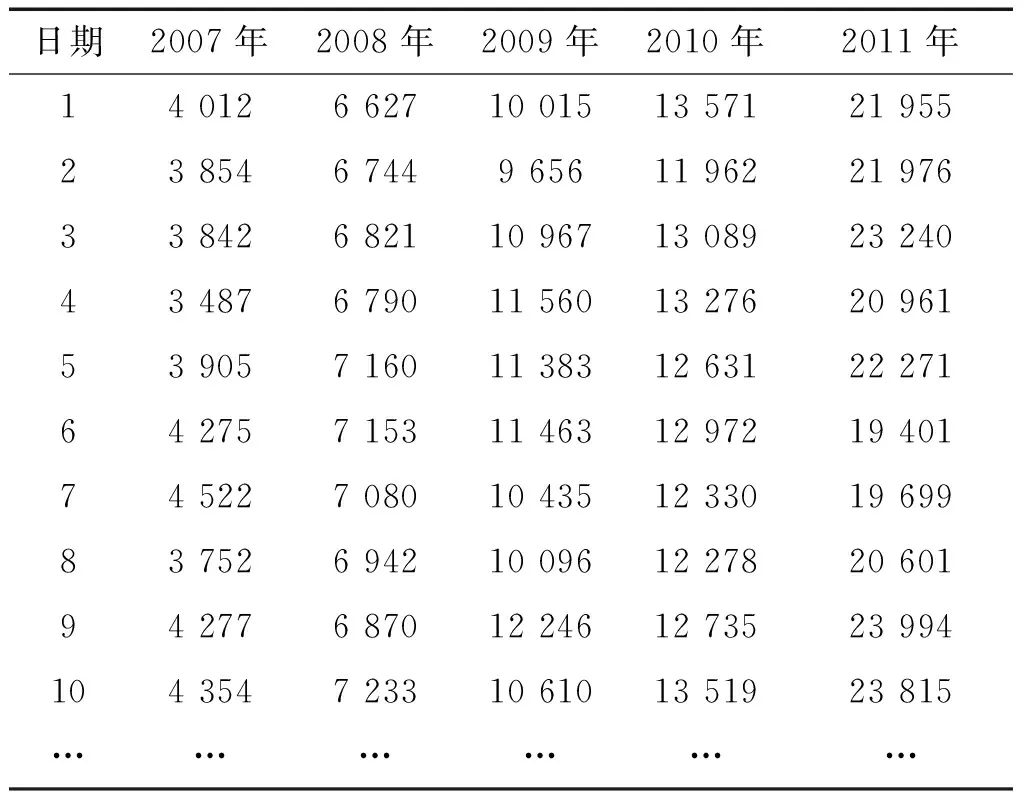
表2 2007—2011年单月每d车辆通行量对比 辆

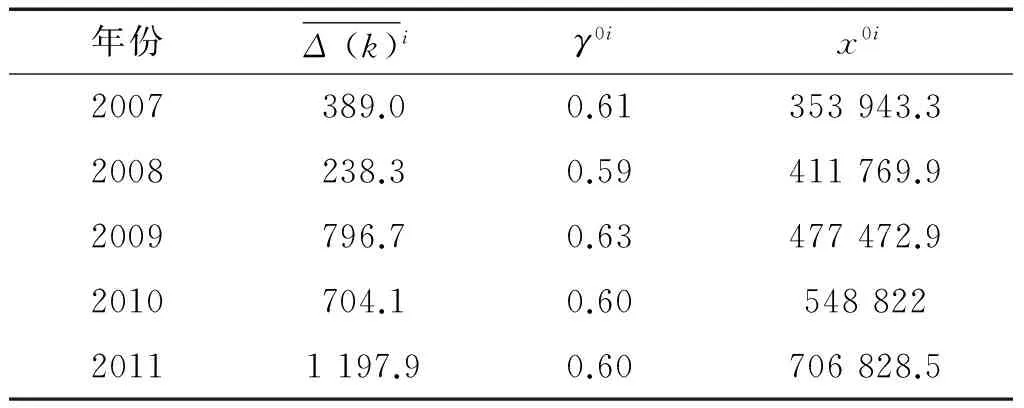
表3 2007—2011年单月“灰度关联度”

由于缺少最后1组预测数据，故表3中γ05取已知γ0i的平均值。

根据公式(9)计算得初始值为：

验证改进灰色GM(1,1)模型预测值为：

为了对比交通量预测的精度，本文采用相对误差作为交通量预测的评价指标。

相对误差计算公式为：

其中，2012年该收费站车辆实际统计数据为1 158 373辆。3种预测模型预测值的相对误差如下：

原始预测模型的相对误差RE1为：

背景值优化预测模型的相对误差RE2为：

改进加权灰色模型的相对误差RE3为：

根据上述结果，可知RE3

3 结束语

由于中长时数据序列急速递增，数据跳跃性较大，为此，本文提出一种改进加权灰色GM(1，1)模型，并将其用于某高速公路收费站的交通量预测。试验验证表明，这种同时优化灰色模型背景值和初始值的预测方法较以往方法大有改进，不仅提高了预测精度，而且还扩大了灰色GM(1,1)模型的应用范围，预测效果明显。

[1]李庆瑞，万发祥，卢 毅．公路交通量预测理论与方法综述[J]．中外公路，2005(6)：151-155．

[2]陈淑燕，王 炜，瞿高峰，等．交通量预测的神经网络集成方法[J]．公路交通科技，2004(12)：80-83+92．

[3]刘宗明，贾志绚，李兴莉．基于灰色马尔科夫链模型的交通量预测[J]．华东交通大学学报，2012(1)：30-34．

[4]钱 超，许宏科，徐 娜，等．基于OLAM的高速公路交通量多维预测研究[J]．交通运输系统工程与信息，2013(2)：48-56．

[5]张新天，罗晓辉．灰色理论与模型在交通量预测中的应用[J]．公路，2001(8)：4-7．

[6]周子兵．灰色理论与模型在交通量预测过程中的缺陷分析[J]．黑龙江交通科技，2005(10)：82+84．

[7]陈涛捷．灰色预测模型的一种拓广[J]．系统工程，1990(4)：50-52．

[8]邓聚龙．灰色系统理论简介[J]．内蒙古电力，1993(3)：51-52．

[9]田 民，刘思峰，卜志坤．灰色关联度算法模型的研究综述[J]．统计与决策，2008(1)：24-27．

[10]张大海，江世芳，史开泉．灰色预测公式的理论缺陷及改进[J]．系统工程理论与实践，2002(8)：140-142．

[11]罗荣桂，陈 炜．灰色模型的一点改进及应用[J]．系统工程理论与实践，1988(2)：46-52．

[12]曾 波，刘思峰，方志耕，等．灰色组合预测模型及其应用[J]．中国管理科学，2009(5)：150-155．

Prediction of Expressway Traffic Volume Based on Optimized Weight Gray GM (1,1) Model

PAN Yong,WU Xiaoli,LI Ke

Targeting at leaping mid/long-term data prediction,this paper put forwards an optimized weight gray GM (1,1) model to forecast traffic volume of expressway toll station. After the first-order weakening and 1-AGO processing of the original traffic volume data,using grey correction to assign weight optimization to the value of initial value,in the same time,the background value is smoothened to make a new grey GM (1,1) model. In this paper,actual traffic statistics of a toll station is used to verify the algorithm predication accuracy of the new gray GM (1,1) model. The results show that the optimized gray GM (1,1) model has better applicability and accuracy.

Optimized grey GM(1,1) model; traffic volume predication; weight

10.13607/j.cnki.gljt.2016.06.028

广东省交通运输厅科技计划项目(2015-02-028)

2016-08-26

潘 勇(1988-)，男，湖北省荆州市人，硕士研究生，助工。

1009-6477(2016)06-0131-04

U491.1+4

A