铁路枢纽站地铁列车运行图的衔接优化
2017-01-06胡倩芸柏赟曹耘文陈垚陈志杰
胡倩芸,柏赟,曹耘文,陈垚,陈志杰
(北京交通大学 城市交通复杂系统理论与技术教育部重点实验室,北京 100044)
铁路枢纽站地铁列车运行图的衔接优化
胡倩芸,柏赟,曹耘文,陈垚,陈志杰
(北京交通大学 城市交通复杂系统理论与技术教育部重点实验室,北京 100044)
分析铁路出站乘客转乘地铁的行为特征与客流规律,以衔接车站乘客总候车时间最小为目标,建立城市轨道交通发车时刻优化模型,并设计相应的遗传算法进行求解。北京地铁7号线案例分析表明,优化后的时刻表能够减少乘客候车时间6.47%,且在铁路列车密集到达的地铁平峰时段,优化效果尤为显著。
城市轨道交通;运行图优化;乘客候车时间;遗传算法
城市客运综合交通枢纽如北京西站是城市客运系统中的重要节点,具有联系城市对外交通和市内客运交通的功能[1]。由于大型铁路客运站的客流到达和输送较为密集,运输能力较大的地铁在其集疏运体系中具有重要的作用。地铁列车的时刻表与干线铁路列车到达时刻的衔接质量直接影响乘客的候车时间和车站内的聚集人数,对运输服务水平有着重要的影响[2]。考虑到车站和区间断面客流呈现明显的早晚高峰特征,我国多数城市的地铁线路按不同时段分别编制行车计划。由于多数车站的客流到达基本服从均匀分布,城市轨道交通系统在同一时段内一般采用等间隔发车的平行运行图[3]。对于衔接铁路枢纽站的地铁线路,其进线客流规律与干线铁路列车的到达时刻密切相关,并不服从均匀达到的规律[4]。为了减少乘客等待时间,提高运营公司的服务水平[5-6],在编制这类线路的列车时刻表时需对铁路枢纽站转乘地铁的客流规律做特殊考虑。 在既有地铁列车运行时刻表研究方面,Assis等[7]以运营成本和服务水平同时最优为目标,综合考虑旅客的舒适性、可用车底数和列车运行时间等限制因素,提出了运行图的编制模型与算法。Barrena等[8]提出动态需求下的铁路非周期列车时刻表优化模型。近些年,国内运行图优化问题的研究重点也逐渐从降低企业运营成本慢慢转向提高服务水平。牛惠民等[9-11]将动态客流需求引入城市轨道交通,分析客流需求随时间变化的规律和乘客在车站的等待行为,并以乘客等待时间最小为目标,建立了多种情况下的列车开行方案优化模型。陈胜波等[12]总结了城市轨道交通断面客流在时间和空间上的一般规律,将旅客乘车感受纳入出行成本,建立以乘客出行成本最小和企业运营成本最小的双目标优化模型。汪波等[13]以最小化城市轨道交通平峰时期乘客换乘的总等待时间为目标,建立网络化情况下的城市轨道交通列车运行图编制模型。Sun等[14]将客流需求的动态性引入地铁中,建立以乘客总等待时间最小为目标的发车时刻优化模型。在运行图优化研究方面,既有研究多数局限于城市轨道交通系统内部,即使是时刻表的衔接问题也限于城市公共交通系统内[15-16],对于铁路衔接的客运枢纽站并未做充分考虑。故本文首先研究铁路出站乘客转乘地铁的行为特征与客流规律,在此基础上建立地铁列车发车时刻的优化模型及算法,以减少乘客等待时间,提高轨道交通服务水平。
1 基于铁路到达时刻的客流规律分析
由于列车到达时间是离散的,铁路出站客流呈现出较强的脉冲性。旅客出站后转乘地铁,会依次经过安检处和售检票处。安检系统和售检票系统的通过能力限制将会对地铁进站客流规律产生较大的影响。本文在刻画客流规律时,先假设没有安检和售检票对客流规律产生影响,即理想条件下的到站客流规律,之后将安检和售检票系统的影响逐步添加至理想客流规律中,对其做出修正以获得符合实际的客流规律。
1.1 理想条件下的客流规律
由于人的步行速度存在差异,所以假设铁路出站客流服从正态分布[17]。在[0,T]时段内,无能力约束下铁路转乘地铁客流的站台到达规律如式(1)所示。
(1)
式中:A1(t)表示理想条件下在第t个时段到达站台的乘客数量;PT表示[0,T]时段由铁路列车转乘地铁的总进站量;KT表示其到达旅客能够在[0,T]时段内顺利转乘地铁的干线铁路到达列车数;σi(t)表示第i列铁路列车转乘地铁的乘客中,在第t个时段抵达地铁站台的客流比例,取值服从标准正态分布。
其中对于任意的σi(t),仅在Ti+ts≤t≤Ti+ts+tinf时按标准正态分布取值,其余情况下σi(t)取0;式中的Ti表示第i列铁路列车的到达时刻,ts表示理想状况下从铁路转乘地铁最快的转乘时间,tinf表示一趟干线铁路列车对地铁进站客流产生影响的持续时长。
1.2 安检及售检票处能力约束下的客流规律
安检对于客流规律的影响主要体现在通行能力的限制。对于每一个单位t,安检处的最大通行能力为r,则其调整规则如下:
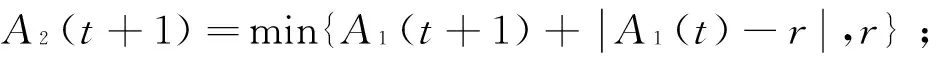
2)若A1(t)≤r,则不做调整。
对于上述的调整规则,此处用函数G(x)来表示,则通过安检调整后的客流A2(t)的表达式为:
A2(t)=G(A1(t))
(2)
乘客通过安检以后需要验票进站,此时客流将分为一卡通进站客流和购票客流。这二者的主要区别在于购票乘客在时间上滞后于一卡通进站乘客。此时需要对客流再做调整,调整如下:
A3(t)=μA2(t)+(1-μ)A2(t-t0)
(3)
式中:A3(t)表示调整后在第t个时段到达站台的乘客数量;μ表示进站客流中一卡通进站的客流比例;t0表示现场购票乘客比一卡通进站乘客的平均延误时间。
将上述公式融合,即可得到基于铁路列车到达时刻的客流规律求解模型,公式如下:
(4)
2 基于进站客流规律的地铁列车发车时刻优化模型与算法
本文将研究时段[0,T]划分为若干个极小的时间间隔,用t表示(t=1,2,3,4…)。对于每个t,假设乘客都在该间隔末同时到达。同时,假设没有留乘现象,即抵达站台的乘客均能顺利乘上即将到达的下趟列车。
基于上述假设,以枢纽站乘客总候车时间最小为目标建立优化模型:
(5)
S.t. Fj-Fj-1≥hmin
(6)
Fj-Fj-1≤hmax
(7)
(8)式中:N表示在[0,T]内发出的车次数;hmin和hmax分别表示最小、最大发车间隔;Fj表示第j列车离开车站的时刻;A(t)表示在第t个时段到达的乘客数;x1(t)为0-1变量,表示在第t个时段末是否有车从枢纽站发出,1表示有,0表示无。
上述模型形式简单,可行域庞大,为了兼顾优化效果与计算时间,本文采用了遗传算法对模型进行求解。遗传算法(GA)是模拟达尔文生物进化论中遗传机理和自然选择的生物进化过程的计算模型[18]。它能通过反复迭代搜索,快速寻找到全局最优解(或准最优解)。其基本原理是从初始种群开始,按照适者生存和优胜劣汰的原则,逐代演化产生出越来越好的近似最优解。本文采用的遗传算法搜索流程如图1。
本文染色体采用特殊的二进制编码方法,每个基因位置对应研究时段内地铁在枢纽站的一个可能的发车时刻,其中“1”表示在该时刻列车发车,“0”表示不发车。取15 s为间隔单位,每个研究时段为1 h,则列车在枢纽站有240个可能的发车选择,即染色体长度为240。算法中其他过程均按照标准遗传算法(SGA)执行。
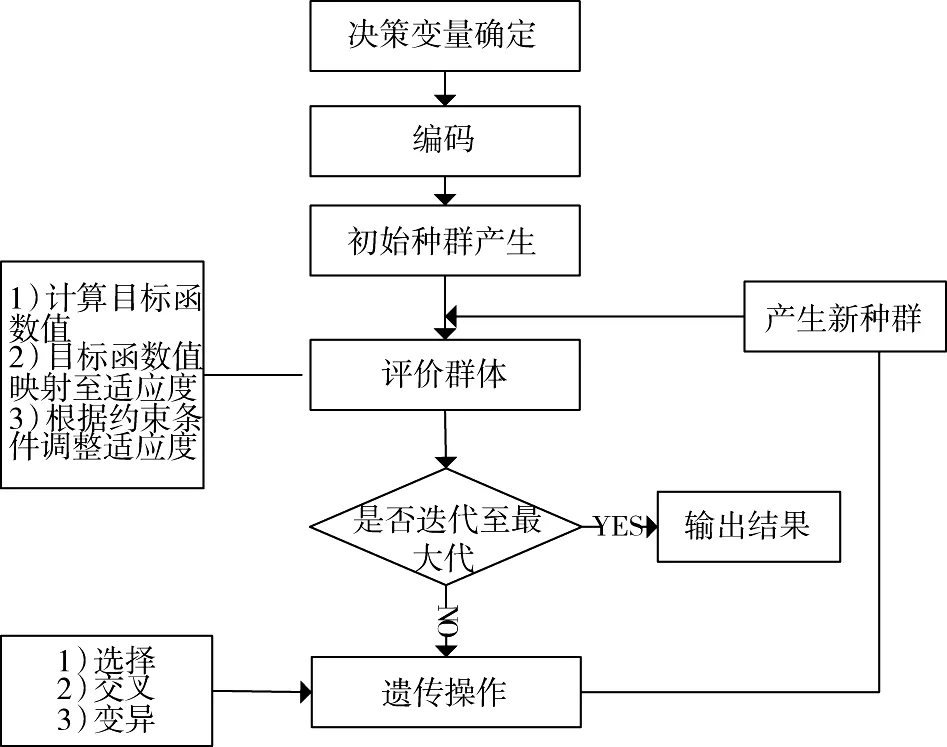
图1 遗传算法程序逻辑Fig.1 Flow chart of Genetic Algorithms
3 案例分析
选取衔接北京西站的地铁7号线为例进行案例分析。优化前的初始运行图采用基于最大断面客流的等间隔平行运行图,其编制基本过程如下。首先根据最大断面客流数据,结合发车间隔的上下限要求,确定全日小时开行列车对数。之后将小时开行的车次数等间隔铺画至运行图中。
在优化初始运行图前,需分析北京西站铁路转乘地铁的客流规律。为了分析不同时段的优化效果,分别选取北京西站某工作日平峰时段12∶30-13∶30,同日高峰时段7∶30-8∶30以及节假日平峰时段12∶30-13∶30作为研究时段。首先以工作日平峰时段为例,依据北京西站干线铁路列车到达时刻对客流A(t)做如下处理,t取15 s间隔。
3.1 理想条件下客流规律
北京西站相关参数设置如表1所示。

表1 相关参数取值Table 1 Parameters value
由前文模型可得到无约束情况下的抵达站台的客流规律,如图2(a)所示。
3.2 安检及售检票的约束
对于安检的通行能力,《地铁设计规范中》并没有规定。参考部分文献中的数据[17],并结合北京西站的具体情况,假设平均每人通过安检的时间为3 s,而地铁北京西站有4个进口,每个进口设置了2台安检设备,则对于每个间隔t其最大的通行能力为40,调整结果如图2(b)所示。
通过安检后需要刷卡进站,现假设每名乘客平均的滞后时间为3 min,两者的客流比例为1∶1。对安检后的客流数据再次调整即可得到最终的到站客流规律,如图2(c)所示。
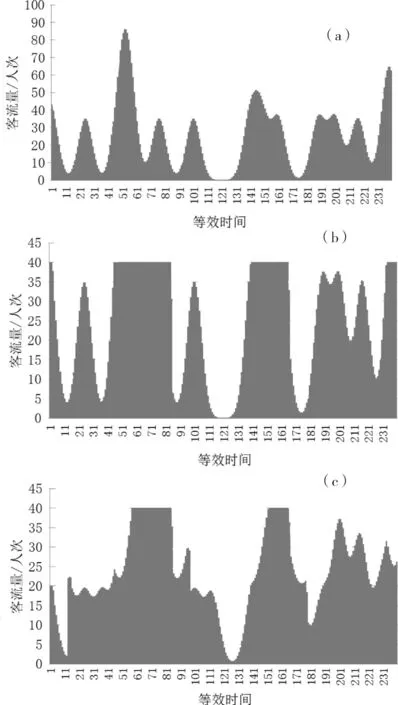
(a)理想条件下客流规律;(b)安检约束后客流规律(c)地铁站台客流到达规律图2 工作日12∶30-13∶30时段北京西站铁路转乘地铁客流规律Fig.2 Passenger flow law from railway to subway in Beijing Western Railway Station during 12∶30-13∶30 in weekday
同理,可利用模型得到其余2个时段的客流规律,如图3所示。
北京地铁7号线与9号线均在此设站,本文假设7号线的客流分担率取为50%。
用于模型求解的遗传算法参数设置如下:初始种群规模500,最大迭代次数5 000,交叉概率0.9,变异概率0.1,优化结果如表2所示。
结果表明,与现行的等间隔发车相比较,通过对发车时刻的调整可以有效减少乘客的总候车时间。在3个研究时段中,工作日平峰时段优化效果最明显,可达6.47%,验证了本文模型与算法的有效性。
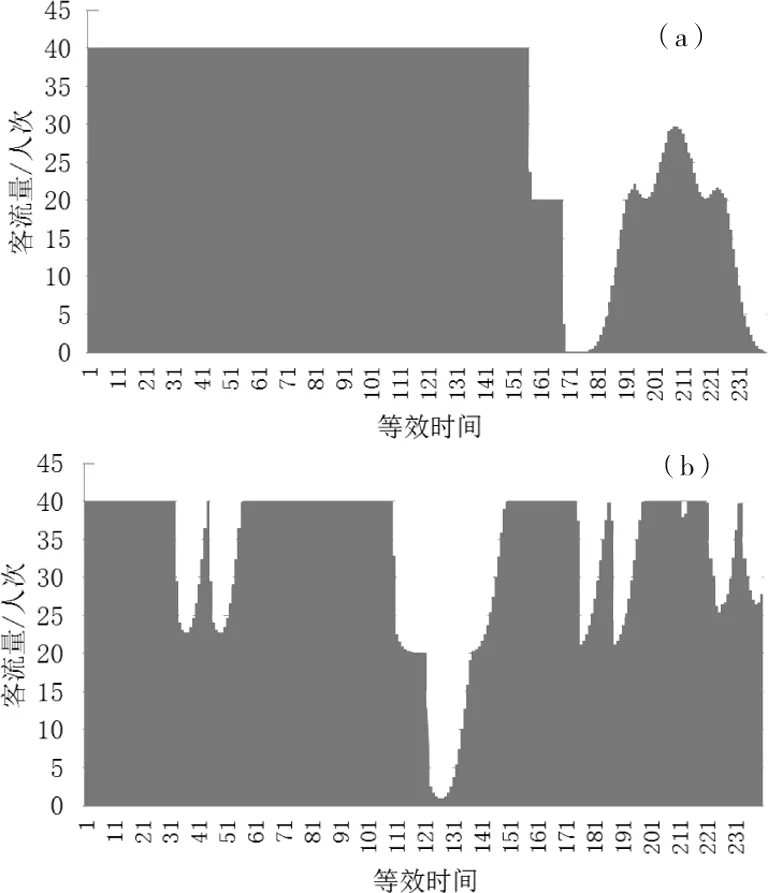
(a)工作日7∶30-8∶30高峰时段到站客流规律;(b)节假日12∶30-13∶30平峰时段到站客流规律图3 工作日高峰和节假日平峰时段到站客流规律Fig.3 Passenger flow law during peak hour in weekday and off-peak hour in holiday
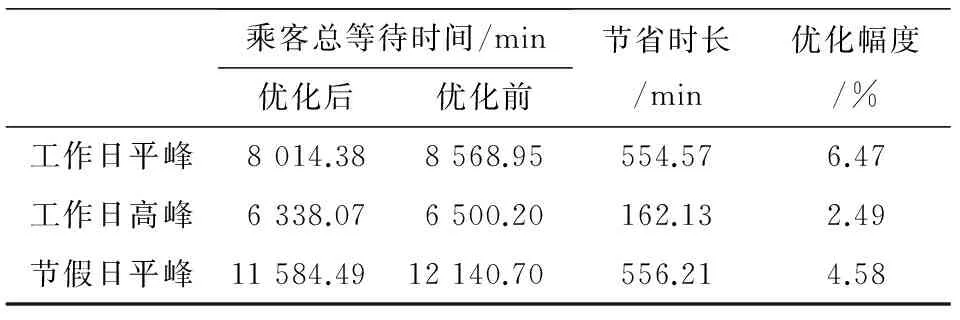
表2 优化结果Table 2 Optimization results
从表2可以看出,乘客总候车时间的优化幅度与发车频率和客流脉冲强度有较大的关系。在工作日高峰时段,地铁发车频率较高,乘客等待时间短,可供调整的优化空间较小,因而优化效果较小;在节假日平峰时段,地铁总进站客流量较大,安检的瓶颈能力突显,客流脉冲性被大幅削弱,优化效果也相应减弱。而在铁路干线列车密集到达的平峰时段,客流脉冲性较强,地铁发车频率相对较小,模型的优化效果最佳。
4 结论
1)分析铁路车站转乘地铁的站台到达客流规律,建立以乘客总候车时间最小为目标的发车时刻优化模型,并采用遗传算法求解。案例分析表明,本文提出的方法可以减少乘客总候车时间达6.47%。
2)研究干线铁路与城市轨道交通时刻表的衔接,提出的方法考虑列车追踪间隔等实际约束,优化后的运行图有较强的实用性。但是限于时间和精力,本文未考虑干线铁路的列车延误可能,下一步将考虑研究晚点列车运行调整策略的动态生成。
[1] 王振报,陈艳艳,韩冬. 城市客运交通枢纽建设时序优化方法[J]. 吉林大学学报(工学版),2012(4):899-903. WANG Zhenbao, CHEN Yanyan, HAN Dong. Optimization method of project construction scheduling for intermodal hub [J]. Journal of Jilin University (Engineering and Technology Edition), 2012(4):899-903.
[2] 陈君福.铁路客运站与城市轨道交通换乘衔接研究[D].北京:北京交通大学,2010. CHEN Junfu. Study on transfer between railway passenger station and urban mass transit [D]. Beijing: Beijing Jiaotong University, 2010.
[3] 王俊杰,谭倩,王璞. 城市轨道交通客流突增研究[J]. 铁道科学与工程学报,2015,12(1):196-202. WANG Junjie, TAN Qian, WANG Pu. Analysis of surging passenger flow in urban rail transit network [J]. Journal of Railway Science and Engineering, 2015,12(1):196-202.
[4] 李得伟,韩宝明,李海鹰. 大型铁路客运站旅客集散微观仿真[J]. 中国铁道科学,2009,30(3):119-124. LI Dewei, HAN Baoming, LI Haiying. Microscopic Simulation on Large Scale Railway Station of Passenger Mustering and Evacuation [J]. China Railway Science, 2009,30(3):119-124.
[5] Ceder A. Methods for creating bus timetables [J]. Transportation Research Part A: General, 1987, 21(1): 59-83.
[6] Ceder A. Bus timetables with even passenger loads as opposed to even headways [J]. Transportation Research Record: Journal of the Transportation Research Board, 2001 (1760): 3-9.
[7] Assis W O, Milani B E A. Generation of optimal schedules for metro lines using model predictive control [J]. Automatica, 2004, 40(8): 1397-1404.
[8] Barrena E, Canca D, Coelho L C, et al. Single-line rail rapid transit timetabling under dynamic passenger demand [J]. Transportation Research Part B: Methodological, 2014, 70: 134-150.
[9] 牛惠民,陈明明,张明辉.城市轨道交通列车开行方案的优化理论及方法[J].中国铁道科学,2011,32(4):128-133. NIU Huimin, CHEN Mingming, ZHANG Minghui. Optimization theory and method of train operation scheme for urban rail transit [J]. China Railway Science, 2011,32(4):128-133.
[10] Niu H, Zhou X. Optimizing urban rail timetable under time-dependent demand and oversaturated conditions [J]. Transportation Research Part C: Emerging Technologies, 2013, 36: 212-230.
[11] Niu H, Zhou X, Gao R. Train scheduling for minimizing passenger waiting time with time-dependent demand and skip-stop patterns: Nonlinear integer programming models with linear constraints [J]. Transportation Research Part B: Methodological, 2015, 76: 117-135.
[12] 陈胜波,何世伟,何必胜.客流波动条件下城市轨道交通列车开行方案研究[J].城市轨道交通研究,2013,16(10):53-58. CHEN Shengbo, HE Shiwei, HE Bisheng. Train service planning for urban rail transit with passenger fluctuation [J]. Urban Mass Transit, 2013, 16(10):53-58.
[13] 汪波,韩宝明,战明辉,等. 城市轨道交通网络周期运行图编制研究[J]. 铁道学报,2013,35(4):9-15. WANG Bo, HAN Baoming, ZHAN Minghui, et al. Study on formulation of periodic train diagram of urban rail transit network[J]. Journal of the China Railway Society, 2013, 35(4):9-15.
[14] Sun L, Jin J G, Lee D H, et al. Demand-driven timetable design for metro services[J]. Transportation Research Part C: Emerging Technologies, 2014, 46: 284-299.
[15] 禹丹丹,韩宝明,董宝田,等. 基于换乘协同的轨道交通网列车时刻表优化模型[J]. 中国铁道科学,2015,36(4):129-135. YU Dandan, HAN Baoming, DONG Baotian, et al. Optimization model of train timetable for rail transit network based on transfer synchronization[J]. China Railway Science, 2015,36(4):129-135.
[16] 邓连波,高伟,赖天珍,等. 基于换乘网络的城市轨道交通关联公交接驳线网优化[J]. 铁道科学与工程学报,2012,9(6):77-83. DENG lianbo, GAO Wei, LAI Tianzhen, et al. Optimal design of feederbus network related to urban rail transit based on transfer network [J]. Journal of Railway Science and Engineering, 2012,9(6):77-83.
[17] 刘俊伯. 高速铁路与城市轨道交通换乘设施通过能力匹配研究[D].北京:北京交通大学,2014. LIU Junbo. Quantitative analysis on the passage bottlenecks through the entrances and exits of Beijing Subway Stations[D]. Beijing:Beijing Jiaotong University, 2014.
[18] 段玉倩,贺家李. 遗传算法及其改进[J]. 电力系统及其自动化学报,1998(1):43-56. DUAN Yuqian, HE Jiali. Genetic algorithm and its improvement [J]. Proceedings of the EPSA, 1998(1):43-56.
Optimization of subway timetable at the railway-subway transfer station
HU Qianyun, BAI Yun, CAO Yunwen, CHEN Yao, CHEN Zhijie
(MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology, Beijing Jiaotong University, Beijing 100044, China)
This paper analyses the passenger's behaviors and flow characteristics within the transferring from railway to subway. A train departure time adjustment model is proposed to minimize passenger's waiting time and Genetic Algorithm is applied to attain the optimal solution. A case study on Beijing Metro Line 7 shows that the proposed model is able to save 6.47% of passengers’ waiting time and the time saving is more significant in the off peak hours when mainline trains arrived at railway stations intensively.
metro system; timetable optimization; passenger waiting time; genetic algorithm
2016-02-04
国家重点基础研究发展规划(973计划)项目 (2012CB725406);国家自然科学基金资助项目 (71571016)
柏赟(1985-),男,湖南人,副教授,从事城市轨道交通运输组织研究;E-mail:yunbai@bjtu.edu.cn
U116
A
1672-7029(2016)12-2503-05
