基于收益最大化的铁路保价运输费率研究
2017-01-06冯芬玲汤子文
冯芬玲,汤子文
(中南大学 交通运输工程学院,湖南 长沙 410075)
基于收益最大化的铁路保价运输费率研究
冯芬玲,汤子文
(中南大学 交通运输工程学院,湖南 长沙 410075)
分析市场占有率的预测模型,运用logit市场分担率模型,选择服务水平和费率计算广义费用,分析铁路保价运输的市场占有率,计算铁路保价运输的收益,以铁路保价运输收益最大化为目标,得到铁路保价运输的最优费率。最后,通过算例分析,验证了模型的可行性。
收益最大化;保价;费率
铁路保价运输工作是铁路运输服务的重要组成部分,对铁路运输安全和自身发展做出了巨大的贡献。随着社会经济的发展,运输市场结构、货主对运输及衍生产品的需求都发生一定程度的变化,货物运输保险市场拓展力度的不断增加,铁路保价运输面临着新的市场环境和严峻的挑战。目前,对铁路保价费率的研究相对较少,除谢如鹤等[1]基于保价费率的7个等级,研究了模糊评价法确定铁路保价运输货物的适用费率,并通过实证论证该方法的有效性,之后就没有研究铁路保价费率的相关文献。在保险费率制定领域,制定保险费率最重要的方法是根据损失发生概率及大小,从而制定保险费率,一般有运用历史数据直接统计法和风险评估法[2-5]。由于铁路保价运输的主要成本为货运安全固定成本投入,投资规模大影响范围广,但具体投入难以精确计算,与保险费率有所区别。随着我国经济进入新常态,市场宏观经济不景气,导致大宗货物的量价齐跌,铁路货运量的下滑和铁路保价运输货物价格的下降使得铁路保价运输市场压力较大,再加上铁路货运保险的竞争,铁路保价运输遇到了前所未有的压力。为了应对复杂的市场环境,铁路保价运输管理部门开始实行费率浮动策略,以提高铁路保价运输市场竞争力。因此,研究铁路保价运输与铁路货运保险之间的竞争关系,优化铁路保价运输费率,为铁路保价运输费率浮动提供理论依据,对提高铁路保价运输市场竞争力和铁路保价运输服务的发展具有重要的意义。
1 市场占有率的计算
1.1 市场占有率模型
预测市场占有率的模型有很多,主要分为宏观分析和微观分析两大类,方法有基于神经网络的市场占有率预测模型[6-7]、基于马尔科夫链的市场占有率预测模型[8-10]和基于微观市场分析的占有率模型[11-13]等。
基于神经网络的市场占有率预测模型是一种与背景无关,能直接模拟市场选择机制的预测市场占有率模型,通过运用神经网络预测模型对市场占有率进行宏观预测,从而得到市场占有率模型。神经网络预测需要大量原始数据的输入,通过自适应学习得到较好的结果,铁路保价运输市场占有率历年数据较多,但影响市场占有率的因素较少,系统自适应学习效果不理想,得到的市场占有率预测结果也一般。
基于马尔科夫链的市场占有率预测模型能预测市场中各个时间点的占有率,分析市场占有率的变动过程,最后得到市场占有率模型。基于马尔科夫链的市场占有率预测模型需要计算系统状态转移矩阵,即必须了解铁路保价运输和铁路货运保险客户之间的转移概率,由于铁路保价运输和铁路货运保险不属于必需品,还需考虑客户两者都不购买的可能性,准确预测客户的转移概率较困难。
logit模型以因果观点为主要出发点,认为一个行为或者一个选择结果的出现是由许多因素共同作用而造成。Logit模型从效用最大化的角度出发,通过对微观个体选择行为的分析,预测整体出现的概率[14]。Logit模型通过分析产品的效用而研究市场占有率情况,过程清晰简单,不需要太多历史数据,目前在交通领域应用较多[15-16]。
1.2 logit模型
目前,铁路货运保险虽然不是由一家保险公司提供,但是由于不同保险公司提供的铁路货运保险产品的替代性较强,本文不考虑保险公司之间竞争关系,市场上只有铁路保价运输和铁路货运保险2种方式(i=1,2)可供货主选择,所以,铁路保价运输和铁路货运保险之间的关系为寡头垄断关系;在经济新形势下,铁路货运量下滑幅度较大,铁路货运市场转为买方市场,铁路货主作为理性经济人,在一定的社会、经济条件的约束下,总是选择认为对自己效用最大的方式。在铁路保价运输和铁路货运保险竞争中,运用logit模型分析市场占有率比较合适。
Logit模型中,2种不同方式的市场占有率与铁路保价运输管理部门和保险公司所采取的竞争策略有关,即2种方式的市场占有率只与其广义费用有关,可用函数表示为:
Pri=f(Vi)
(1)
式中:Pri为铁路保价运输或者铁路货运保险的市场占有率;Vi为铁路保价运输或者铁路货运保险的广义费用,当铁路保价运输管理部门和保险公司采取一定的价格策略和产品策略时,Vi可表示为:
Vi=f(Pi,Fi)
(2)
式中:Pi为铁路保价运输或者铁路货运保险的价格策略;Fi为铁路保价运输或者铁路货物保险的服务水平。
根据随机效用理论为基础的离散选择模型,货主选择铁路保价运输或者铁路货运保险的随机效用可以表示为:
Ui=Vi+εi, i=1,2…N
(3)
设εi是随机项,且随机项εi相互独立并且都服从Gumbel分布,则铁路保价运输或者铁路货运保险的竞争模型可用多项式logit流量分配模型描述,即铁路保价运输或者铁路货运保险被选择的概率为:
(4)
其中:Pi-=min(P1,P2)

1.3 广义费用函数
本文选择运输方式的安全性、时效性、合理性和便捷性作为竞争力影响因素进行分析。Si表示安全性指标,货物安全是货主选择铁路保价运输和铁路货运保险的最终目的;Ti表示时效性指标,体现货主选择铁路保价或者保险服务所花费的时间;Zi表示合理性指标,合理性体现的是服务被货主接受的程度,属于货主的主观感受,主要包括服务受理合理性和货损理赔合理性,服务受理合理性体现的是受理服务信息的准确情况以及合同条款的合理性,直接影响货主对服务的认知情况,理赔合理性主要指货损认定情况和赔付金额情况,决定货主对服务的最终印象;Hi表示便捷性指标,便捷性指标主要受服务的手续和流程的影响,体现的是服务全程的便捷情况,主要分为受理便捷性和理赔便捷性,其中受理便捷性主要体现在服务受理的方式以及流程的便利程度,而理赔便捷性主要受提赔流程和提赔材料的影响。
则服务水平函数Fi可表示为:
(5)
式中:ωi(i=1,2,3,4)表示各项服务水平影响因素的权重系数。权重系数是指各个决策指标在整体中价值的高低和相对重要的程度以及所占比例的大小量化值,本文采用层次分析法确定各指标的权重,设层次分析法归一化后的权重λ。
由于各指标所使用的量纲不同,为了避免“大数吃小数”现象,需要对各指标进行量纲一致化,指标值越小服务水平越高型指标量纲一致化函数为:
(6)
指标值越大服务水平越高型指标量纲一致化函数为:
(7)
根据经济学中需求曲线的特点,随着价格的降低和服务水平的提高,货主对服务的认可度越高,由于价格与服务之间没有相关性,因此,本文采用线性函数来定义运输方式的广义费用函数,可假设广义费用Vi与价格Pi和服务水平Fi之间的关系如下所示:
Vi=-θ1Pi+θ2Fi
(8)
式中:θi>0(i=1,2)是模型参数;θ1为价格对市场占有率的影响参数;θ2为服务水平对市场占有率的影响参数。运用矩估计法,确定模型参数θi(i=1,2)的值。
2 铁路保价运输收益最大化模型
2.1 最大化模型的建立
当铁路货运保险价格P2为固定值时,即当铁路货运保险公司采取不变的价格策略和服务策略时,铁路保价运输收益为:
(9)
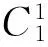
2.2 收益最大化模型的求解
铁路保价运输费率是有铁路保价运输管理部门根据实际需要制定的,从1992年实施铁路保价运输服务至今,铁路安全形势取得了较大的进步,铁路保价运输基本费率还没有调整。根据现代营销学理论,价格策略是营销策略的重要组成部分,费率对铁路保价运输总收益影响很大,即计算铁路保价运输收益函数取最大值时的费率。
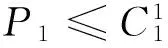
当P1≥P2时:Pi-=min(P1,P2)=P2
(10)


(11)
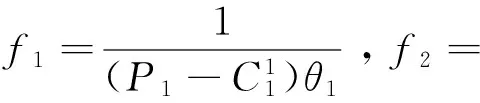


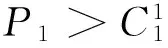
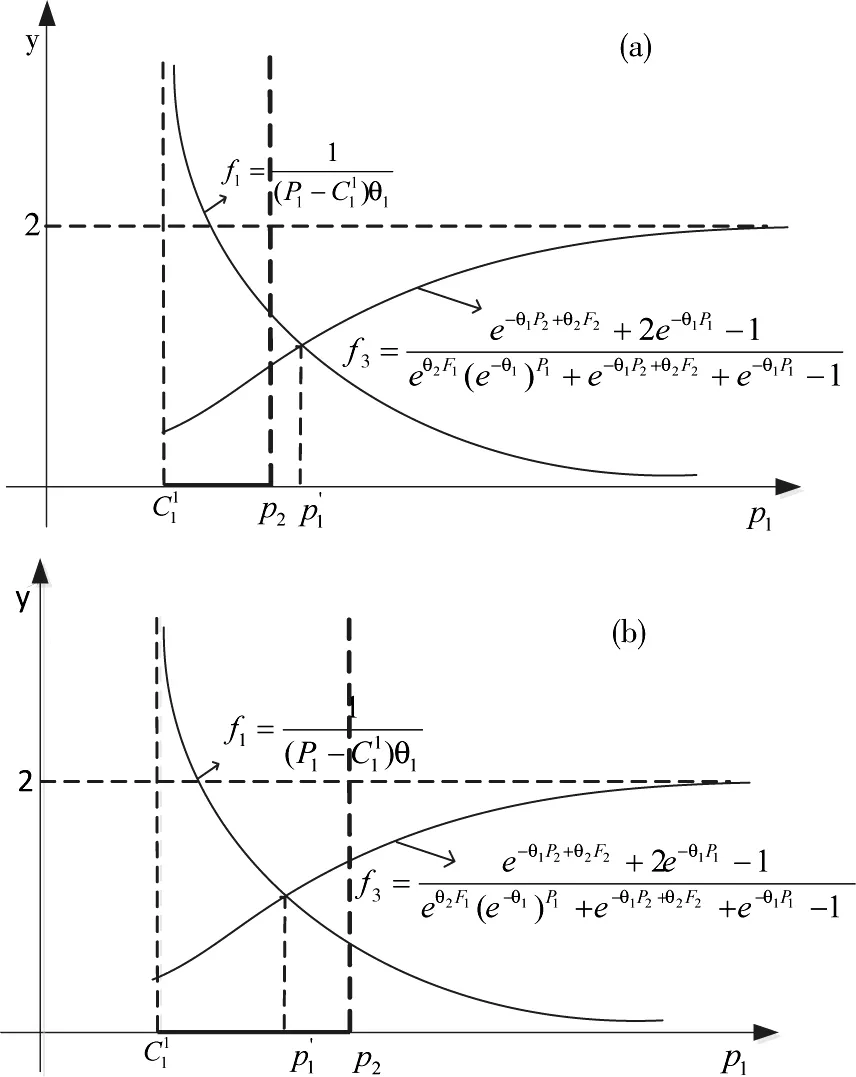
(12)

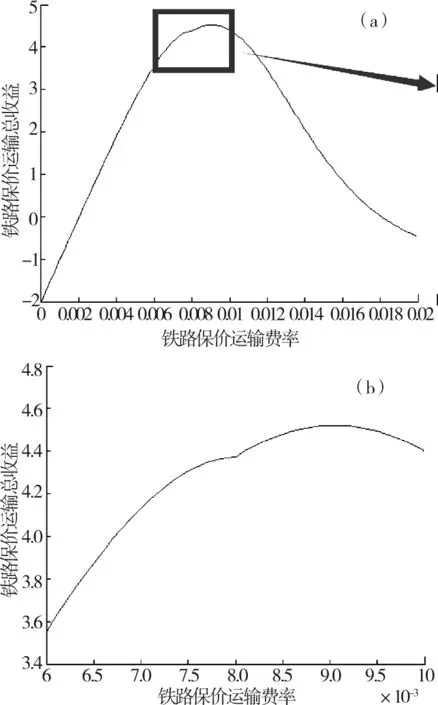
(a)当P1*≥P2时;(b)当P1* (12) (13) 当P1 (14) (15) (16) (a)当时;(b)当时图2 函数f1和函数f3示意图Fig.2 Diagram of function f1 and function f3 (17) (18) 国内不同保险公司货运保险价格以协议价格为主,考虑到铁路货运种类多样,本文以包裹为例分析铁路保价费率,假定保险费率为0.8%,保价费率为1%。根据我国铁路赔偿补偿情况分析,假定保价运输变动成本为总金额的0.1%,由于铁路货运保险一般属于代办类,变动成本较保价运输高,货运保险的变动成本为总金额的0.15%。近几年我国铁路保价运输批保价率虽然达到70%以上,但是考虑不足额保价的影响,假定我国铁路保价运输市场占有率取值为60%,铁路货运保险的市场占有率为20%。 铁路保价运输和铁路货运保险的效用是指从消费者的角度2种服务的不同效用,所以,铁路保价运输和铁路货运保险的安全性、时效性、合理性以及便利性4个指标主要是通过问卷调查获得,考虑到货主选择的简便性,采取5分制,分别对应非常不满意,不满意,一般,满意,非常满意5个等级。根据对121位货主的现场询问和短信调查,对数据进行分析计算,铁路保价运输安全性、时效性、合理性和便利性的平均得分分别是4.6分,2.8分,3.3分和4.1分,而铁路货运保险由于营销不足,铁路货主对铁路货运保险了解不足,对铁路货运保险评价不高,安全性、时效性、合理性和便利性的平均得分分别是3.7分,3.2分,3.1分和2.0分。 根据专家打分法对影响服务水平的安全性、时效性、合理性以及便利性4个因素进行打分,可得判断矩阵pλ,根据层级分析法随机一致性指标检验,计算并归一化之后得到各因素的权重: 根据以上数据,得到铁路保价运输和铁路货运保险的服务水平分别为: F1=0.799 3,F2=0.614 4 广义费用Vi为: V1=-θ1P1+θ2F1=-0.01θ1+0.799 3θ2,V2= 所以,θ1,θ2分别为: θ1=394.894 8,θ2=10.213 1 根据前面求到的参数,代入铁路保价运输总收益函数,可得铁路保价运输的总收益为: 图3 铁路保价运输市场占有率Fig.3 Market share of value-guaranteed goods in railway transportation 如图3所示,随着铁路保价运输费率的增加,铁路保价运输市场占有率处于下降趋势,且下降速度与铁路保价运输费率有关。铁路保价运输费率较低时,由于铁路保价运输的价格和服务相对于铁路货运保险具有较大的优势,铁路保价运输市场占有率下降较慢;铁路保价运输费率较高时,由于铁路运输的价格和服务相对于铁路货运保险等已经完全不具有优势,选择铁路运输服务的客户相对较少,铁路保价运输市场占有率下降较慢;当铁路保价运输费率在[0.006 0.014]间波动时,由于铁路保价运输、铁路货运保险之间的价格和服务差距相对较小,市场占有率受铁路保价运输费率的影响较大,铁路保价运输市场占有率下降较快。 (a)铁路保价运输总收益曲线;(b)铁路保价运输总收益曲线局部放大图示图4 铁路保价运输总收益曲线Fig.4 Yield curve of value-guaranteed goods in railway transportation 如图4(a)所示:随着铁路保价运输费率的增加,铁路保价运输总收益总体呈现先快速增加后减少的趋势,在铁路保价运输费率较低时,铁路保价运输费率的上升对铁路保价运输收益增加的影响大于铁路保价运输市场占有率下降对铁路保价运输总收益减少的影响,所以铁路保价运输总收益整体呈现上涨趋势;随着铁路保价运输费率的进一步增加,铁路保价运输费率的上升对铁路保价运输收益增加的影响小于铁路保价运输市场占有率对铁路保价运输总收益的减少的影响,铁路保价运输总收益整体呈现下降趋势。 如图4(b)可知,铁路保价运输费率在铁路货运保险费率0.008处连续但不可导,根据前面对铁路保价运输总收益的分析,铁路保价运输总收益在0.008前后都出现极大值可能性,根据《铁路保价费率浮动管理办法》第7条,保价费率浮动时最小浮动单位为0.1‰,当铁路保价运输费率不变时: π1(0.01)=4.340 0 计算在其他条件不变的情况下,铁路保价运输最佳费率:当P1<0.008时,铁路保价运输总收益对铁路保价运输费率的导函数为: 当P1≥0.008时:铁路保价运输总收益对铁路保价运输费率的导函数为: 综上,在不考虑铁路货运保险公司策略变动的情况下,铁路平均保价运输费率可以适当下调至0.009 1,费率下降0.9‰,从而使铁路保价运输总收益最大,即铁路保价运输费率相对下降9%,而铁路保价运输总收益则上升4.2%。 1)通过分析市场占有率模型的优劣,考虑铁路保价运输的实际情况,指出logit模型在铁路保价运输工作中的实用性。 2)通过计算铁路保价运输和铁路货运保险的广义费用,基于logit市场分担率模型研究保价运输市场占有情况;再从铁路保价运输收益最大化分析铁路保价运输的最佳费率情况。 [1] 谢如鹤,陈治亚.用模糊评估法确定铁路货物保价费率[J].铁道学报,1998,20(3):7-11. XIE Ruhe,CHEN Zhiya. Determination on charge rate of value-guaranteed goods in railway transportation with fuzzy estimation method[J]. Journal of the China Railway Society,1998,20(3):7-11. [2] Barry K Goodwin. An empirical analysis of the demand for multiple peril crop insurance[J]. American Journal of Agricultural Economics, 1993,75(2):425-434. [3] Borg R F. Pitfalls in builder’s risk insurance for temporary structures in construction[J]. Practice Periodical on Structural Design & Construction, 2014:153-155. [4] 王丽红, 杨华, 田志宏,等. 非参数核密度法厘定玉米区域产量保险费率研究——以河北安国市为例[J]. 中国农业大学学报, 2007, 12(1):284-284. WANG Lihong, YANG Hua, TIAN Zhihong, et al. Maize GRP rate of premium deciding by nonprarametric kernel density:A case study on Anguo city, Hebei province[J]. Journal of China Agricultural University, 2007, 12(1):284-284. [5] 田玲, 姚鹏. 地震保险费率厘定研究[J]. 北京理工大学学报(社会科学版), 2013, 15(3):54-59. TIAN Ling ,YAO Peng. The pricing of china’s earthquake insurance[J].Journal of Beijing Institute of Technology(Social Sciences Edition) , 2013, 15(3):54-59. [6] 贺力群, 朱克强. 企业市场占有率预测神经网络模型[J]. 北京理工大学学报, 1998(6):670-673. HE Liqun, ZHU Keqiang. A neural network model for market share prediction[J]. Journal of Beijing Institute of Technology, 1998(6):670-673. [7] 尹钢, 邓飞其, 叶其革. 基于自组织模糊神经网络的市场占有率模型[J]. 华南理工大学学报(自然科学版), 2004, 32(9):17-22. YIN Gang, DENG Feiqi, YE Qige. A market share model based on the self-organized fuzzy neural networks[J]. Journal of South China University of Technology (Natural Science Edition), 2004, 32(9):17-22. [8] 孙红丽, 何永贵, 张文建,等. 马尔科夫模型在企业人力资源供给预测中的应用[J]. 华北电力大学学报, 2004, 31(5):56-58. SUN Hongli, HE Yonggui, ZHANG Wenjian,et al.Application of markovmodel in human resource supply forecasting in enterprises[J]. Journal of North China Electric Power University, 2004, 31(5):56-58. [9] 牛东晓, 关哲, 任峰,等. 基于马尔科夫过程的电力企业市场竞争预测[J]. 华北电力大学学报, 2004, 31(1):66-68. NIU Dongxiao,GUAN Zhe, REN Feng. et al. Market percentage perdieiton based on Markov chain in electrie power enter priseeom petition[J]. Jouranl of Notrh Chian Eecltrci Power Unviesity, 2004, 31(1):66-68. [10] 肖谦, 赵海燕. 基于马尔科夫模型的物流服务市场占有率的预测[J]. 湖南社会科学, 2014(4):132-134. XIAO Qian, ZHAO Haiyan. Forecast of the market share of logistics service based on Markoiv model[J]. Social Sciences in Hunan,, 2014(4):132-134. [11] 谢如鹤, 邱祝强, 李庆云,等. Logit模型在广深铁路客流分担率估算中的应用[J]. 中国铁道科学, 2006, 27(3):111-115. XIE Ruhe, QIU Zhuqiang, LI Qingyun, et al. Application of logit model in estimating the distribution rate of passenger flows on Guangzhou— Shenzhen Railway[J]. China Railway Science, 2006, 27(3):111-115. [12] 马波涛, 张于心, 赵翠霞. 运用Logit模型对高速客流分担率的估计[J]. 北京交通大学学报, 2003, 27(2):66-69. MA Botao, ZHANG Yuxin, ZHAO Cuixia. Estimation of the distributing rates of high-speed passenger flows with the logit model[J]. Journal of Northern Jiaotong University, 2003, 27(2):66-69. [13] 黄劲松, 赵平, 王高,等. 基于顾客角度的市场占有率研究[J]. 中国管理科学, 2004, 12(2):95-101. HUANG Jinsong, ZHAO Ping, WANG Gao, et al. Market share research based on customer orientation[J]. Chinese Journal of Management Science, 2004, 12(2):95-101. [14] 陈锟, 朱敏, 王晓红. Logit模型在个体选择行为中的研究演进[J]. 统计与决策, 2006(20):138-140. CHEN Kun, ZHU Min, WANG Xiaohong. The research evolution of Logit model in individual choice behavior[J]. Statistics & Decision, 2006(20):138-140. [15] 金安. LOGIT模型参数估计方法研究[J]. 交通运输系统工程与信息, 2004(1):71-75. JIN An. On methodology of parameter estimation in LOGIT model[J]. Journal of Transportation Systems Engineering and Information Technology, 2004(1):71-75. [16] 何宇强, 毛保华, 陈团生,等. 高速客运专线客流分担率模型及其应用研究[J]. 铁道学报, 2006, 28(3):18-21. HE Yuqiang, MAO Baohua, CHEN Tuansheng. et al. The mode share model of the high-speed passenger railway line and its application[J]. Journal of the China Railway Society, 2006, 28(3):18-21. Research for charge rate of value-guaranteed in railway transportation based on benefit maximization FENG Fenling, TANG Ziwen (School of Traffic and Transportation,Central South University,Changsha 410075,China) By using logit model and selecting service level and rate to calculate generalized cost, this paper analyzes the market share of railway in value-guaranteed. Then the optimal rate can be obtained for the maximization of revenues of value insured rail traffic.Finally ,the rationality of this model is demonstrated through the analyses of numerical example. benefit maximization; value-guaranteed; charge rate 2016-01-29 中国铁路总公司科技研究开发计划课题(2015F024) 冯芬玲(1973-),女,河北邯郸人,副教授,博士,从事交通运输规划与管理研究;E-mail:FFL0731@163.com U29-3 A 1672-7029(2016)12-2508-08
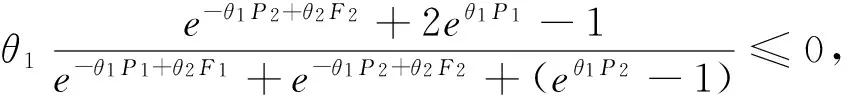

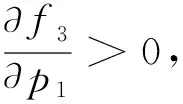

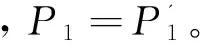
3 算例分析

-θ1P2+θ2F2=-0.008θ1+0.614 4θ2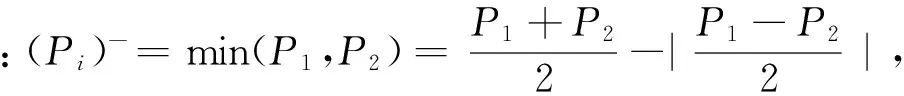

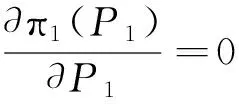
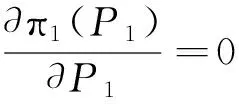
4 结论
