SH波作用下地表软覆盖层中浅埋圆孔的动力分析

赵元博， 齐 辉， 丁晓浩， 赵栋栋

(哈尔滨工程大学 航天与建筑工程学院，哈尔滨 150001)

SH波作用下地表软覆盖层中浅埋圆孔的动力分析

赵元博， 齐 辉， 丁晓浩， 赵栋栋

(哈尔滨工程大学 航天与建筑工程学院，哈尔滨 150001)

利用复变函数法和波函数展开法对地表软覆盖层中浅埋圆形孔洞在稳态SH波作用下的动应力集中问题进行了研究并给出了解析解。根据SH波散射时的衰减特性，采用了大圆弧假定的方法，即利用一个半径很大的圆来近似表示地表覆盖层的直线边界，将半空间覆盖层直线边界问题转化为曲面边界问题。首先根据Helmholtz定理预先给出了待求波函数的一般形式解，再根据边界条件并利用复数Fourier-Hankel级数展开的方式把所求问题转化为求解波函数中未知系数的无穷线性代数方程组问题，对该无穷代数方程组截取有限项求得该问题的数值结果。通过算例分析了SH波垂直入射时，覆盖层和半空间介质的波数差异、覆盖层厚度的变化、圆孔埋置深度等因素对地表软覆盖层中浅埋圆形孔洞周边动应力集中系数的影响。

地表软覆盖层；圆形孔洞；SH波散射；大圆弧假设；动应力集中

随着经济社会的发展和城市建设的加快，城市中的地下工程越来越多，地下工程的抗震安全性对国民经济和社会的正常运转有着极为重要的作用，特别是自1995年日本阪神地震后，地下结构的抗震研究越来越受到人们的重视[1-2]。

在地下结构抗震研究中，波动方法是一种重要的理论研究方法[1-2]。20世纪70年代，PAO等[3]在专著中详细介绍了利用波函数展开法对不同形状的物体在稳态和瞬态应力荷载下的动应力集中现象的研究结果。此后，LEE等[4-5]将其应用到半空间问题，对圆形隧道的平面SH波散射问题进行了研究。刘殿魁等[6]将解决静态应力集中问题的复变函数方法拓展到动态领域。目前对半空间内各种缺陷及其界面问题的研究已取得很多成果[7-8]，此处不再一一列举。但是在实际工程中，由于土层的分层以及每层的厚度、刚度等特性都是千变万化的，因此传统的半空间模型并不能完全反映实际问题。对带有覆盖层的半空间问题，由于波在覆盖层中会发生多次的反射和折射，且存在着波形转换以及覆盖层中产生面波等问题，散射波场很难构造，一直是比较棘手的问题。LEE等[9]采用大圆弧假定的方法给出了半空间中单个圆形孔洞对P波和SV波散射的解析解，将传统的直边界问题转为曲线边界问题，从而使问题得以简化。齐辉等[10-11]在此基础上研究了地表覆盖层的存在对半空间内单、多个圆孔、圆夹杂受平面SH波作用时的散射和动应力集中系数的影响，结果都表明，地表覆盖层的存在对半空间内的圆形缺陷在SH波作用下的散射和动应力集中问题都有很大的影响，在实际工程中必须予以重视。

文献[10]和文献[11]的研究中，各种缺陷都存在于半空间中，而目前在我国的地下工程施工中，对浅埋结构大量采用先直接开挖后回填的方式，很多时候回填土的压实处理往往不够严谨，因此会在地表形成一个含有孔洞等介质的软弱土层。本文在前人的基础上，利用大圆弧假定的方法对地表软覆盖层中单个圆形孔洞在SH波作用下的动应力集中问题进行了研究。

1 理论分析

1.1 问题模型

(1)

图1 模型示意图Fig.1 Schematic diagram of the model

1.2 控制方程

本文研究的是出平面剪切运动的SH波的散射问题。在直角坐标系中，在X-Y平面内，SH波产生的位移场可以表示为W(X,Y,t)，该位移场与Z轴无关，且垂直于X-Y平面。对于稳态问题，位移场W(X,Y,t)需要满足以下Helmholtz方程：

(2)

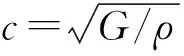
直角坐标系下的应力应变关系为：

(3)

(4)

在复平面内，式(2)～(4)可以表示为：

(5)

(6)

(7)

在复平面极坐标系下，式(6)、(7)可以表示为：

(8)

(9)

1.3 入射波场及应力

(10)

(11)

(12)

1.4 散射波场及应力

(13)

(14)

(15)

(16)

(17)

(18)

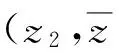
(19)

(20)

(21)

式中：⊗=z2+i(RD+h2)

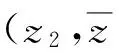
(22)

(23)

(24)

(25)

(26)

(27)

式中：⊕=z1-i(RD+h2)

(28)

(29)

(30)

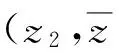
(31)

(32)

(33)

式中：⊙=z2+i(RD+h2)

1.5 连接条件

(34a)

(34b)

(34c)

(34d)

将入射波和各个散射波的波场与径向应力表达式代入上式，并将已知量挪到等号右边，未知量挪到等号左边，可得：

(35)

其中：

η1=-W0exp[ik1Re(z1e-iα0)]

•=z1-i(RD+h2)

*=z2+i(RD+h2)

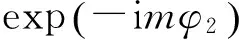
(36)

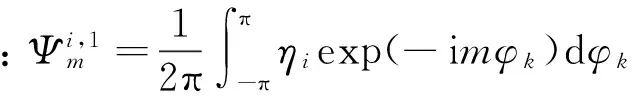
i,j=1,2,3,4，当i=1,2,4时，k=1；当i=4时，k=2。

这样就可求出系数An、Bn、Cn、Dn将其代入位移和应力的表达式中，截取有限项，便可得到所求的各种未知量了。

1.6 动应力集中系数(DSCF)

#=z2+i(RD+h2)

2 算例分析

为了便于分析，定义如下参数组合：G*=G1/G2，ρ*=ρ2/ρ1，k*=k2/k1，各量之间关系为：k*k*=ρ*G*。当k*>1时，表明区域Ⅰ比区域Ⅱ“硬”，即入射波由“硬”半空间入射，而此时孔洞位于“软”的地表覆盖层中。本文中所有的k*均大于1，所有的ρ*均取0.8。由于在本算例中所有结果均为无量纲结果，因此假定孔洞的半径r=1。

图2给出了在SH波垂直入射时，G*=k*=ρ*=1，k1=0.1，h1为1.5r和12r时圆孔边的动应力集中系数。由于G*=k*=ρ*=1，此时区域Ⅰ和区域Ⅱ的参数相同，因此覆盖层下边界TD不存在，区域Ⅰ和区域Ⅱ融为一体，问题退化为半空间均匀介质中单个圆孔对SH波的散射问题。数值结果表明，当Rd≥120r时，DSCF的结果与文献[12]中图6的结果完全一致，这也验证了大圆弧假设方法的合理性。

图3～图5给出了当α0=90°，ρ*=0.8 ，h1=1.5r，h2=1.5r，k*=1.3、1.4、1.5、1.6时，而k1分别为0.5、1、1.5时，圆孔边的DSCF，此时G*分别为2.112 5、2.45、2.812 5、3.2。

图2 ρ*=G*=k*=1时圆孔边动应力集中系数Fig.2 DSCF around circular cavity(ρ*=G*=k*=1)

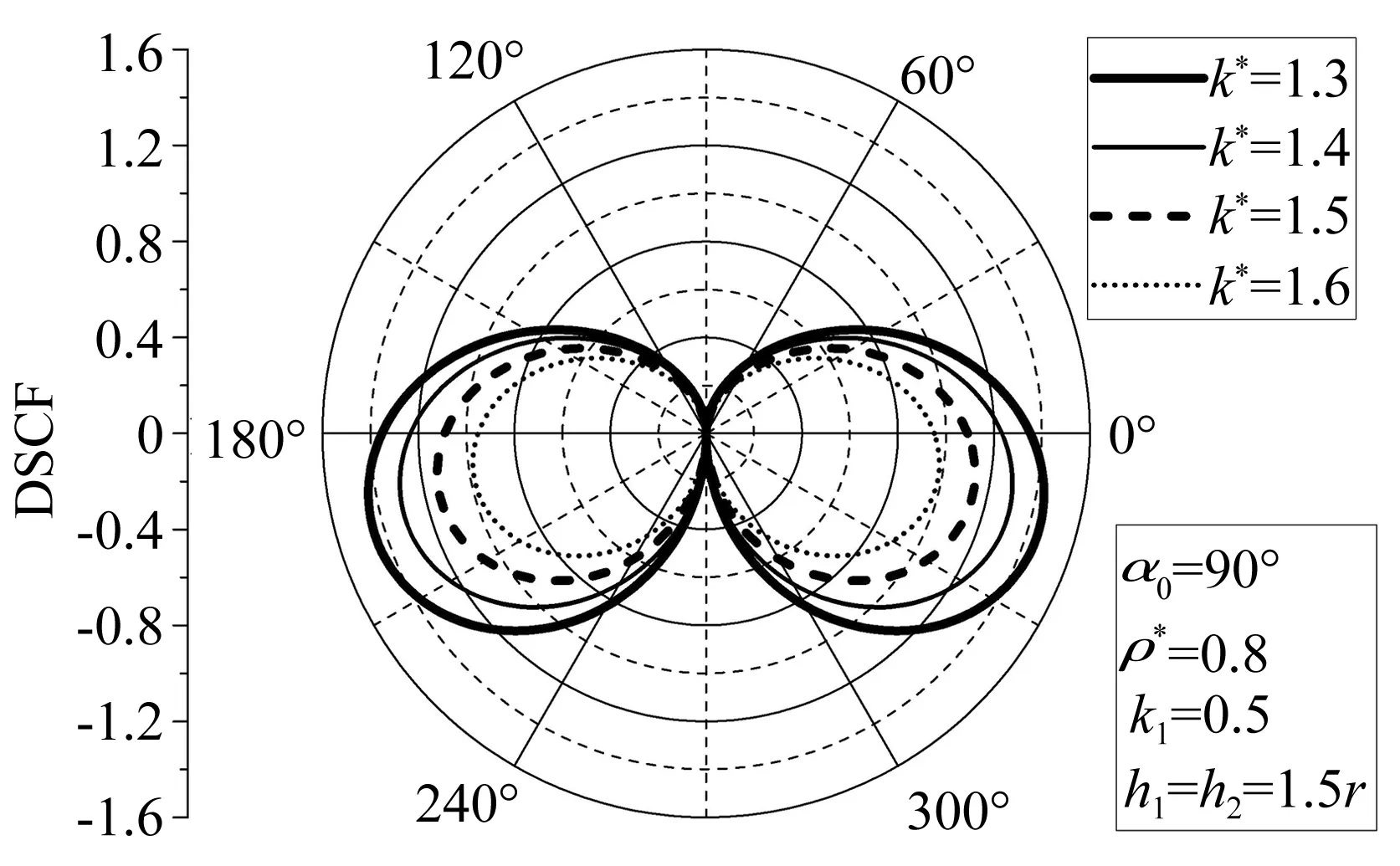
图3 k1=0.5时圆孔边动应力集中系数Fig.3 DSCF around circular cavity(k1=0.5)

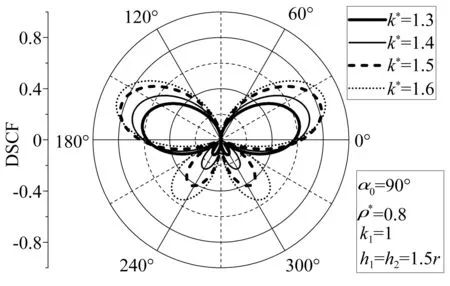
图4 k1=1时圆孔边动应力集中系数Fig.4 DSCF around circular cavity(k1=1)

图5 k1=1.5时圆孔边动应力集中系数Fig.5 DSCF around circular cavity(k1=1.5)

从图3可以看出，当k1=0.5时，即入射波在低频段入射时，DSCF的形状近似为椭圆形，随着k*的增，DSCF随之减小，且减小是线性的。当k*以0.1为增量增加时，MAX DSCF不断减小，每次约缩小0.18，当k*=1.6时，MAX DSCF已经略小于1，但其所在位置(角度)则没有变化，都是在195°和345°两处。

在图4中，k1=1，此时SH波在中频段入射。与图3不同，此时DSCF的图形变为蝴蝶形。随着k*的不断增大，DSCF不是一直减小而是不断增大，但变化不是线性的，从k*=1.3到k*=1.5，增量是不断变大的，但从k*=1.5到k*=1.6，增量却突然减小。随着k*的不断增大，MAX DSCF所在位置(角度)也持续做小幅变化，从大约15°和165°逐渐上移为大约20°和160°。

在图5中，k1=1.5， SH波在中高频段入射，此时图形比较复杂，变化的规律性较差。虽然DSCF的形状也是蝴蝶形，但和图4不同，图5中四个象限内每一部分的大小都基本相当。当k*从1.3增大到1.5时，DSCF是在不断减小的，其中k*为1.4和1.5时DSCF非常相近，当k*为1.6时，DSCF又突然变大。而MAX DSCF所在位置(角度)却随着k*的增大逐渐从一二象限变为三四象限。

图6给出了当SH波在不同频率入射时，MAX DSCF随k*的变化关系。k1=0.5时，MAX DSCF随着k*的增大先增加后减小，整个变化是均匀光滑的，最大值发生在k*=1.18时，而后基本以相同的斜率缓慢下降；当k1=1时，MAX DSCF先随着k*的增大缓慢减小，在k*=1.32时达到极小值，而后随着k*的增大而逐渐增加，当k*=1.54时达到极大值，此后继续随k*的增大而逐渐减小；k1=1.5时，当k*<1.15时，MAX DSCF与k1=1时的情况基本重合，此后曲线继续下降，并在k*=1.34至k*=1.56之间形成了一个极小值区间，此后曲线逐渐增大并在k*=1.75达到极大值，而后又逐渐下降。

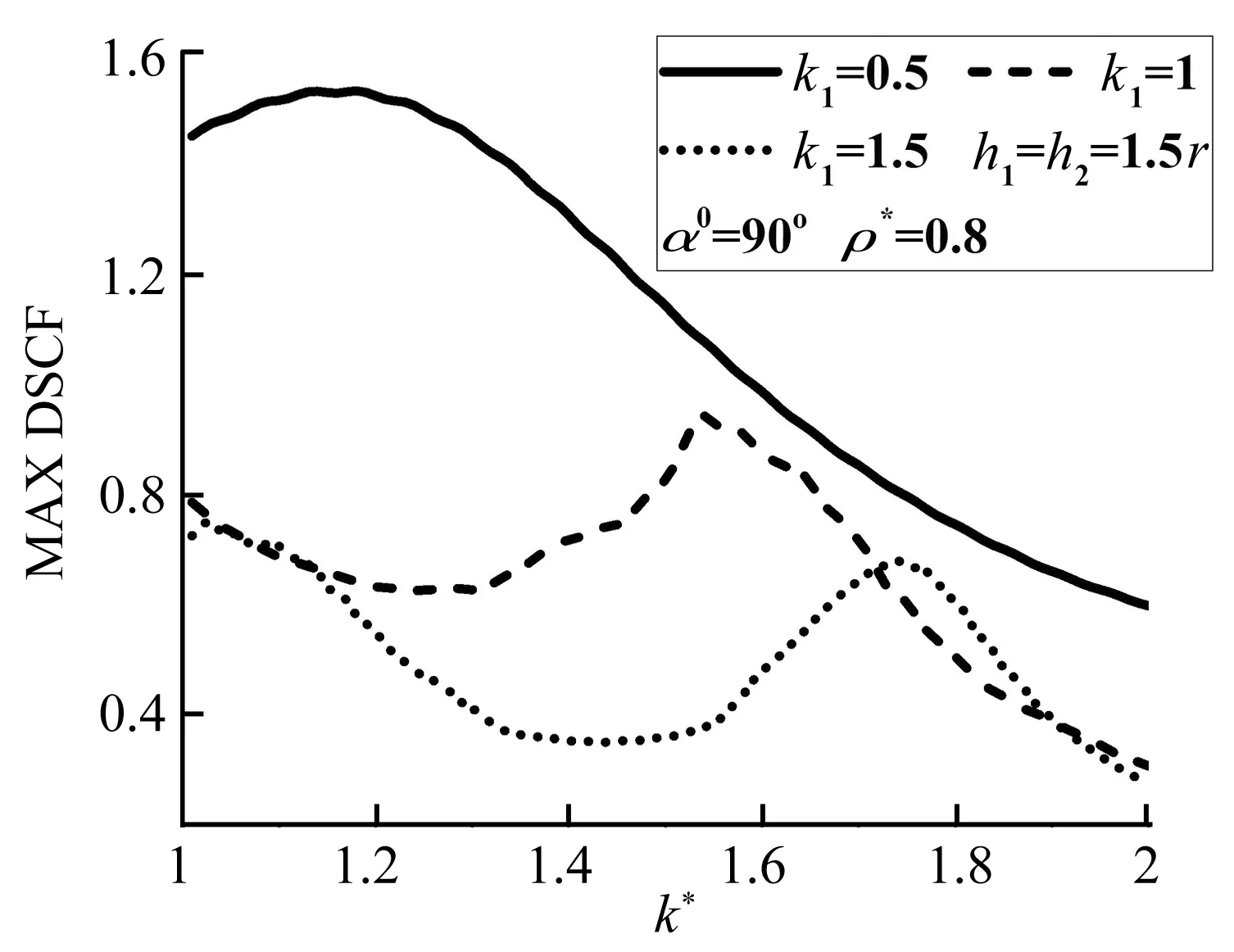
图6 圆孔边动应力集中系数最大值随k*的变化Fig.6 Variation of MAX DSCF around circular cavity with k*

图7给出了当k*确定时，MAX DSCF随k1的变化关系。当k1在0.3附近时，MAX DSCF达到最大值，在此之前以线性方式急剧增大，而此后则随着k1的增大而近乎直线的下降，并在k1=1.0附近达到极小值，此后随着k1的增加而呈现出震荡下降的趋势。整体而言，入射波在低频段入射时的MAX DSCF要大于高频段入射时的情况，k*越大则MAX DSCF达到最大值时的入射频率越小，且MAX DSCF 的最大值也越大，而入射波在中高频段时，MAX DSCF以剧烈震荡的方式逐渐降低。

图7 圆孔边动应力集中系数最大值随k1的变化Fig.7 Variation of MAX DSCF around circular cavity with k1

图3～图5中k1固定而k*取不同值时MAX DSCF的变化情况均在图6～图7中得到体现。综合图3～图7整体来看， SH波低频入射时的MAX DSCF要大于高频入射时的情况。

图8和图9给出了当α0=90°，ρ*=0.8 ，圆孔位于覆盖层正中，k1分别为0.5、1、1.5，而k*分别为1.3和1.8时，MAX DSCF随覆盖层厚度h的增加而变化的情况。图8中G*为2.112 5，图9中G*为4.05。

图8 k*=1.3时圆孔边动应力集中系数最大值随h的变化Fig.8 Variation of MAX DSCF around circular caity with h(k*=1.3)

图9 k*=1.8时圆孔边动应力集中系数最大值随h的变化Fig.9 Variation of MAX DSCF around circular caity with h (k*=1.8)

从图8可以看出，当波数比k*固定时，随着覆盖层厚度h的增加，圆孔边MAX DSCF呈周期性震荡变化。MAX DSCF震荡的周期随入射波数k1的增加而减小，k1=0.5时的周期约是k1=1时的4倍，是k1=1.5时的6倍，此外振幅也随k1的增加而减小。整体而言，入射波数越大，则圆孔边MAX DSCF越小。当k1为0.5时，圆孔边MAX DSCF的峰值呈现出随h的增加而逐渐降低的趋势，尽管下降的趋势较弱，但k1为1和1.5时，这种趋势则基本上看不出来。

通过图9可以看出，与图8一样，圆孔边MAX DSCF呈周期性震荡变化并且随着入射波数k1的增加而减小。由于波数比k*的增大，图9中各个曲线的震荡周期都要比图8中对应的周期短，如k1=0.5时图8中曲线的周期是图9中对应曲线的周期的1.4倍。但MAX DSCF的振幅却要比图8中的大。整体而言，图9中各曲线的取值范围比图8中的要小，而且在图9中，k1为0.5时圆孔边MAX DSCF的峰值随h的增加而逐渐降低的趋势也要弱于图8。

图10和图11给出了当SH波垂直入射(α0=90°)且圆孔埋置深度固定(h1=1.5r)时，圆孔边MAX DSCF随覆盖层厚度h的增加而变化的情况。两图中ρ*=0.8，k1取值为0.5、1、1.5。图10中k*为1.3，G*为2.112 5，图11中k*为1.8，G*为4.05。

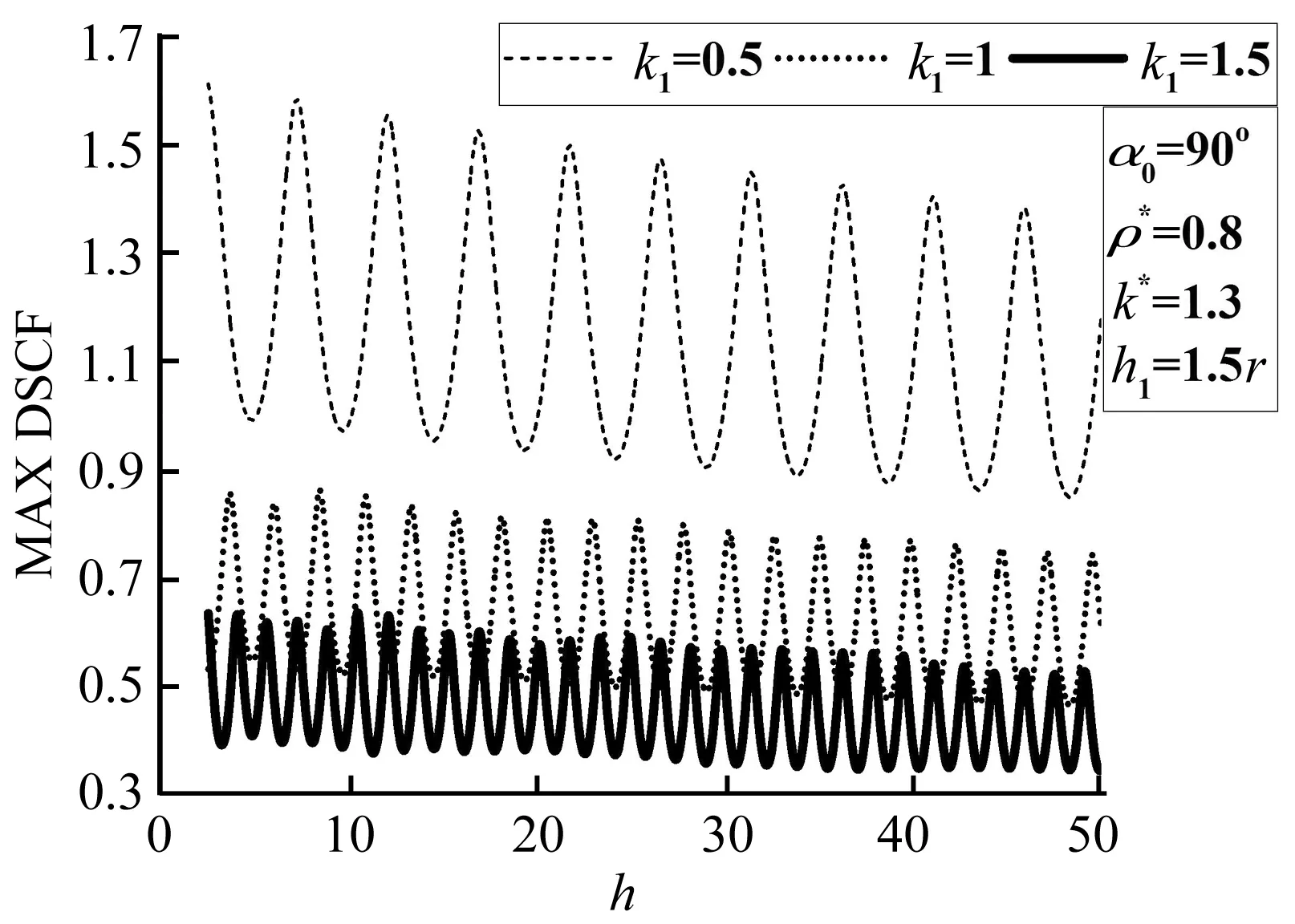
图10 k*=1.3时圆孔边动应力集中系数最大值随h的变化Fig.10 Variation of MAX DSCF around circular caity with h (k*=1.3)

图11 k1=2.4时圆孔边动应力集中系数随h的变化Fig.11 Varation of DSCF around circular caity with h(k1=2.4)

与图8和图9一样，当参数h1固定而参数h不断增加时，图10和图11中圆孔边MAX DSCF也呈周期性震荡变化，周期随k1的增大而减小，但变化规律有很大不同。对比图8和图10可以发现，首先，图10中的变化规律更明显，无论k1取值如何，图10中MAX DSCF都呈现出随着h的增加而震荡下降的趋势，而图8中仅仅k1取值为0.5时才比较明显；其次，图10中各曲线的振幅不但比图8中的小，而且幅值也更稳定，当k1从0.5到1.5时，图10中的幅值分别约为0.6、0.3、0.22，而图8中则分别约为0.4～1、0.4、0.3；再次，当k1为0.5时，图8中的曲线每个周期中还会出现一个极小值，这与图10也是不同的。同样，对比图9和图11也有相同的变换。

综合图8～图11可以看出，当圆孔埋置深度很浅且固定时，随覆盖层厚度的增加，圆孔边MAX DSCF的变规律性要更强。

3 结 论

本文根据复变函数法、波函数展开法、大圆弧假设法对地表软覆盖层中单个圆孔在半空间中入射平面SH波作用下的动应力集中问题进行了研究，将地表覆盖层的上下边界用半径很大的圆弧来近似，以此构造出散射波场，并且得到所求问题的解析解，并通过数值算例分析了SH波垂直入射时，不同的入射波数及波数比、覆盖层厚度、圆孔埋置深度等参数对圆孔周边动应力集中系数的影响。

数值算例表明：

(1)当SH波垂直入射，随着入射频率的逐渐增加(入射波数k1不断增大)，圆孔边动应力集中系数最大值在低频段(k1≈0.3～0.5)达到最大，而后不断下降，并在中频段之后(k1≈0.8～1)以震荡的方式逐渐下降，而且覆盖层与半空间相比越“软”，达到最大值时的入射频率越小。这说明在实际工程中要非常重视SH波低频垂直入射，且覆盖层比半空间“软”的情况。

(2)随着覆盖层厚度的增加，无论圆孔埋置于覆盖层正中还是将其固定于覆盖层浅层位置，圆孔边动应力集中系数的最大值都呈周期振荡变化，且综合而言，入射频率越小则动应力集中系数最大值越大。这表明在工程应用中要根据场地的各种参数来合理选择埋置位置。

能够影响地表覆盖层中的圆形孔洞的动应力集中系数的参数很多，不同的参数变化会导致不同的结果，这说明在对浅埋地下工程的抗震分析中必须对土层间的各项参数进行认真分析，综合考虑各种参数的影响，以便对地下结构进行合理的设计，从而达到理想的结果。

[1] 孙超，薄景山，齐文浩，等. 地下结构抗震研究现状及展望[J]. 世界地震工程，2009, 25(2):94-99. SUN Chao, BO Jingshan, QI Wenhao，et al. Status and prospect of seismic research on underground structures [J]. World Earthquake Engineering, 2009, 25(2):94-99.

[2] 周健，董鹏，池永. 软土地下结构的地震土压力分析研究[J]. 岩土力学，2004, 25(4):554-559. ZHOU Jian, DONG Peng, CHI Yong. Research on seismic soil pressure of underground structures in soft soils [J]. Rock and Soil Mechanics, 2004, 25(4):554-559.

[3] PAO Y H，MOW C C. Diffraction of elastic waves and dynamic stress concentrations [M]. New York: Crane and Russak, 1973: 114-304.

[4] LEE V W. On deformation near circular underground cavity subjected to incident plane SH waves[C] // Proceedings of The application of computer methods in engineering conference. Los Angeles, CA, 1977.

[5] LEE V W, TRIFUNAC M D. Response of tunnels to incident SH-waves[J] . Journal of Engineering Mechanics,ASCE, 1979(105):643-659.

[6] LIU D K, GAI B Z, TAO G Y. Applications of the method of complex functions to dynamic sress concentrations [J]. Wave Motion, 1982, 4(3): 293-304.

[7] 梁建文，魏新磊，VINCENT W L. 圆弧形沉积谷地对平面P波的三维散射解析解[J]．岩土力学，2010，31 (2) : 461-470． LIANG Jianwen, WEI Xinlei，VINCENT W L. 3D scattering of plane P waves by a circular-arc alluvial valley[J]．Rock and Soil Mechanics,2010,31(2) : 461-470．

[8] 杨在林, 刘殿魁, 孙柏涛, 等. 半空间可移动刚性圆柱对SH波散射及动应力集中[J]. 工程力学, 2009, 26(4): 51-56. YANG Zailin, LIU Diankui, SUN Baitao, et al. Scattering of SH-waves and dynamic stress concentration by moving ragid cylinder in half space [J]. Engineering Mechanics, 2009, 26(4): 51-56.

[9] LEE V W, KARL J. Diffraction of elastic plane P wave by circular underground unlined tunnels [J]. European Earthquake Engineering, 1993, 6(1): 29-36.

[10] 齐辉，折勇，陈冬妮. SH波作用下地表覆盖层对浅埋圆孔散射与动应力集中的影响[J]. 哈尔滨工程大学学报，2009, 30(5):513-517. QI Hui, SHI Yong, CHEN Dongni. Scattering of SH-wave in a layered half-space with a subsurface circular cavity [J]. Journal of Harbin Engineering University, 2009, 30(5):513-517.

[11] 陈冬妮，齐辉，赵春香. SH波对覆盖层下浅埋圆孔和圆夹杂的散射[J]. 工程力学，2014, 31(10):40-46. CHEN Dongni, QI Hui, ZHAO Chunxiang. Scattering of SH-wave by subsurface circular cavities and inclusionins a layered half-space [J]. Engineering Mechanics, 2014, 31(10):40-46.

[12] 林宏，刘殿魁. 半无限空间中圆形孔洞周围SH波的散射[J]. 地震工程与工程振动，2002, 22(2):9-16. LIN Hong, LIU Diankui. Scattering of SH-wave around a circular cavity in half space [J]. Earthquake Engineering and Engineering Vibration, 2002, 22(2):9-16.

Dynamic analysis for a shallow buried circular cavity impacted by SH-Wave in a soft layered half-space

ZHAO Yuanbo, QI Hui, DING Xiaohao, ZHAO Dongdong

(College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, China)

The issue of dynamic stress concentration for shallow buried circular cavity in a soft layered half-space under steady SH-wave has been studied based on the complex function and wave function expansion method. An analytical solution was obtained. According to the attenuation characteristic of SH-wave scattering, using the large-arc assumption method, which was, straight boundary of the surface layer was approximated by a circle with large radius, which led to a surface boundary problem. Firstly, the general forms of unknown wave function were given based on the Helmholtz theorem. Then, according to the boundary conditions and the complex Fourier-Hankel series expansion method, the problem was transformed into the infinite linear algebraic equations of unknown coefficients in the solution of the wave function. From the finite terms, the numerical results could be obtained. Through examples, it is analyzed the influence on the distribution of dynamic stress concentration factor around the shallow buried circular cavity in a soft layered half- space when SH-Wave is normal incidence, including the wave number difference between overburden layer and half space medium in different incident frequencies, the variation on the cover thickness and the buried depth of the circular cavity.

soft surface layer; circular cavity; SH-wave scattering; large-arc assumption method; dynamic stress concentration

黑龙江自然科学基金(A201404)

2015-07-15 修改稿收到日期：2015-11-30

赵元博 男，博士生，1982年生

齐辉 男，教授，博士生导师，1963年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2016.24.020