基于时域流形稀疏重构方法的滚动轴承故障特征增强研究

张文清， 何清波， 丁晓喜， 韩 杰， 谢明伟

(1.中国科学技术大学 精密机械与精密仪器系，合肥 230026;2.中国空气动力研究与发展中心 设备设计与测试技术研究所，四川 绵阳 621000)

基于时域流形稀疏重构方法的滚动轴承故障特征增强研究

张文清1,2， 何清波1， 丁晓喜1， 韩 杰2， 谢明伟2

(1.中国科学技术大学 精密机械与精密仪器系，合肥 230026;2.中国空气动力研究与发展中心 设备设计与测试技术研究所，四川 绵阳 621000)

振动信号降噪处理一直是滚动轴承故障诊断中的一个重要的研究内容。利用时域流形和匹配追踪的优点，克服两种方法的不足，提出一种优势互补的新方法——时域流形稀疏重构方法。时域流形具有良好的去噪能力，却由于其非线性的处理过程导致振幅信息不能保持。匹配追踪方法的降噪能力与原子本身有关，由于不能保证选取到最能表征信号的原子，故其降噪能力具有局限性。提出的方法克服了上述问题。首先通过匹配追踪的方法以时域流形结果为基础从一个过完备字典中找到最匹配的原子，之后以得到的原子与原始信号匹配计算获得重构的稀疏系数，最后通过稀疏系数和得到的原子重构信号，该结果同时具有匹配追踪和时域流形的优点。以轴承故障信号分析为例，验证了该方法的有效性。同时和时域流形及匹配追踪方法相比较，结果显示该方法具有明显的优越性。

时域流形；匹配追踪；稀疏重构；滚动轴承故障诊断

振动信号降噪一直是滚动轴承故障诊断中的一个重要研究内容。通过对轴承振动信号的分析，可以实现监控其运行状态、减少停机时间、确保高效生产。

常用的振动信号降噪方法按分析域可分为时域变换去噪、频域变换去噪和时频域变换去噪。时域变换去噪主要是在时域或其线性变换中根据信号和噪声的特点来抑制噪声，如时域平均法。频域变换去噪则主要是设计相应通带的滤波器实现信号去噪，如带通滤波[1-2]。时频分布提供了一个时间-频率的联合分布，在去噪时可以对时间、频率信息进行综合考虑，如基于小波变换以及时频分析的信号去噪方法[3-4]。

Mallat基于小波分析提出了信号可以用一个超完备字典进行表示，从而开启了稀疏表示的先河。流形学习(Manifold Learning)方法在著名杂志《Science》被首次提出以后，成为信息科学领域的研究热点。近几年来，有越来越多的方法应用稀疏表示和流形学习来达到振动信号降噪的目的。本文提出了一种新的信号重构方法，对振动信号进行降噪和特征增强。

信号重构的主要任务是从原始振动信号中提取表征轴承故障的纯瞬态脉冲。和传统的带通滤波法、奇异值分解法(SVD)[5]相比较，稀疏分解是一种非常有效的方法。稀疏分解需要建立一个过完备字典，是通过稀疏原子去除噪声重构故障特征信号的有用工具，如匹配追踪(MP)[6-10]、最佳正交基(Bob)[11]、基追踪(BP)[12]等。近些年随着信号处理领域的发展，稀疏分解在稀疏性和高分辨率上显示出优势。但是，在强背景噪声下的稀疏分解提取故障特征仍然比较困难。另一方面，流形学习[13-16]利用非线性降维方法找出动力学系统在相空间中具有全域正交坐标系的低维主流形，然后根据主流形反求原始振动信号，进而达到降噪的目的。流形学习能够更加有效地消除高斯白噪声，成功提取出淹没在强背景噪声中的故障特征。然而，流形学习结果不能够显式表达，重构信号虽然保留故障特征但幅值失真严重。

本文基于时域信号流形学习和匹配追踪算法，提出一种新方法，称为时域流形稀疏重构，用于去除背景噪声增强故障特征。该方法主要是在对时域信号流形学习得到的主流形上获取稀疏基即原子，通过原子在原始含噪信号上的稀疏表达，实现故障冲击特征的提取和故障信号幅值的恢复。时域流形稀疏重构的结果在噪声抑制的同时能够更好地保持故障脉冲及其幅值，从而增强故障特征，反映滚动轴承故障的本质特性。时域流形稀疏重构提供了一种去除噪声增强故障特征的方法，其效果在后面实验分析中得到了验证。

1 时域流形稀疏重构理论

1.1 时域流形分析

时域流形(Time-domain Manifold, TM)是嵌入在非平稳时域信号中的一种内在的非线性流形结构[17-21]。其基本方法是通过对信号相空间重构(Phase Space Reconstruction, PSR)后的高维数据流形学习，提取出反映信号动力学本质的时域模式。TM揭露了信号非平稳和非线性两种信息，适合于故障特征的提取。

设有一长度为N的信号x(t)，首先通过相空间重构变为一个m维的信号，其第i个相点为

(1)

式中,xi为x(t)的第i个点，m为嵌入维数，τ为延迟时间。此时有高维数据矩阵P∈Rm×n(τ=1,n=N-m+1)，其元素与原始信号x(t)的对应关系如下：

P(j,k)=xk+(j-1)τ

j∈[1,m],k∈[1,n]

(2)

式中，P矩阵为n个m维的相点组成的列向量，也可以看作为m个长度为n的一维时域信号组成的矩阵。当τ=1时，由曹氏方法计算得到m≥10，在本文中m取11，τ取1。对P矩阵做流形学习，得到TM。本文通过局部切空间排列(Local Tangent Space Alignment, LTSA)算法，从m个一维时域信号中计算出d个主流形(d≪m)。LTSA是一个局部到全局变换排列的优化算法，其优化目标函数为

(3)

式中,Ei为每一个点局部重建误差，S为0-1选择矩阵，W=diag(w1,… ,wN),Wj=(I-eeT/k)(I-Θj+Θj) ，Θi为局部坐标矩阵。为了唯一确定流形T，假设TTT=Id，最后有：

B=SWWTST

(4)

对B做特征值分解，最优的流形T对应着B的第2到第(d+1)个最小非零的特征值。

ci=PiT1

(5)

1.2 匹配追踪获取原子

作为一种稀疏分解的方法，匹配追踪(MP)算法能够得到信号在一个过完备字典上的稀疏表示。MP算法的目的是从过完备字典中，选择一个与信号最匹配的原子，构建一个稀疏逼近。如果选择的原子具有适合轴承故障的脉冲特征，那么MP算法对轴承故障特征的提取和降噪将特别有效。通常我们用相关系数来表征原子和被分析信号的匹配程度。相关系数越大，匹配程度越高。

本文用Morlet小波字典做过完备字典。Morlet小波字典可以表示如下：

(6)

(7)

式中,r0为原子在字典中的索引，dr0为此次迭代找到的最匹配原子，R1为第一次迭代后的残值。

其次，对残值R1进行同样的分解，那么经过k次迭代可以得到：

Rk-1=〈Rk-1,drk-1〉drk-1+Rk

(8)

式中,Rk-1和Rk分别为第k-1次迭代和第k次迭代后得到的残值，drk-1为第k次迭代找到的最匹配原子，rk-1为原子drk-1在字典D中的索引。

1.3 信号重构

在采用MP算法搜索原子的过程中，每一步迭代都得到了一个最匹配的原子和新的残值。如果连续5次迭代残值能量变化都小于一个较小的给定阈值ε时，即可认为连续5次得到的最匹配原子表达的均为噪声，此时终止算法，余下的残值中绝大部分为噪声。其迭代终止条件如下：

(9)

式中,Ri、Ri+1为第i次迭代和第i+1次迭代的残值，K为合适的原子数目，ε为一个较小的数，本文取ε=0.02。每次迭代残值能量都会减小。当连续5次迭代残值能量的变化都小于一个较小的数ε时，我们认为已经提取了所有的滚动轴承故障脉冲，剩下的残值能量包含着大量噪声可以忽略，并且当前的原子数目就是能够较好重构信号又不引入过多噪声的最佳原子数目。通过这种方法，我们能够得到重构信号的合适原子数目K，下一步就是用K个原子重构信号x(t)。

ci=〈x,di〉,i=1,2,…,K

(10)

式中,xr为重构后的信号，di为MP算法得到的原子，ci为原始信号x(t)在原子di方向投影系数。这样，我们结合时域流形抑制噪声和稀疏表达降噪的优点，得到了进一步降噪的重构信号，并恢复其真实幅值。

2 仿真分析

为了定量评估时域流形稀疏重构方法在轴承故障特征增强上的效果，本文使用仿真轴承故障信号进行研究分析，如下所述。

根据阻尼自由振动模型，构建如下仿真信号：

xs(t)=x0(t)+n(t)=

sin[2πf0(t-τ·h)]+n(t)

(11)

式中,f0为固有频率，ζ为阻尼系数，τ为脉冲间隔，a为幅值，x0(t)为一个无噪声信号，而n(t) 为高斯随机噪声。

定义一种处理后信号和原始无噪声信号之间的退化的二次残差(Vestigial Quadratic Mismatch,VQM)来评价处理方法的有效性，以dB为结果单位，表达如下：

(12)

式中,xr为处理后信号，x0为原始无噪声信号，E(·)为数学期望。VQM需要知道原始无噪声信号，因此其在仿真研究中有着很好的应用，但对实际振动信号却没用。VQM越小，说明去噪效果越好。

用式(11)生成一段脉冲信号，其中f0=2 500 Hz,ζ=0.005,τ=0.012 5 s,a=1。仿真信号的信噪比为-5 dB。图1(a)仿真信号被噪声污染，图1(b)采用时域流形稀疏重构方法重构信号。很明显，重构信号中噪声已被大大地去除。图1(c)表明，本文方法重构的信号和原始信号在振幅和相位上是匹配的。

图2是不同方法对仿真信号去噪的结果。图2(c)和图2(d)采用本文方法重构的结果，效果显著。图2(e)和图2(f)是时域流形的结果， 流形去除了带内噪

声，但信号幅值信息丢失。图2(g)和图2(h)是MP算法的结果，虽然MP算法的去噪效果也不错，且能够保持幅值信息，但是从时频分布中看出，本文方法去噪效果更佳。

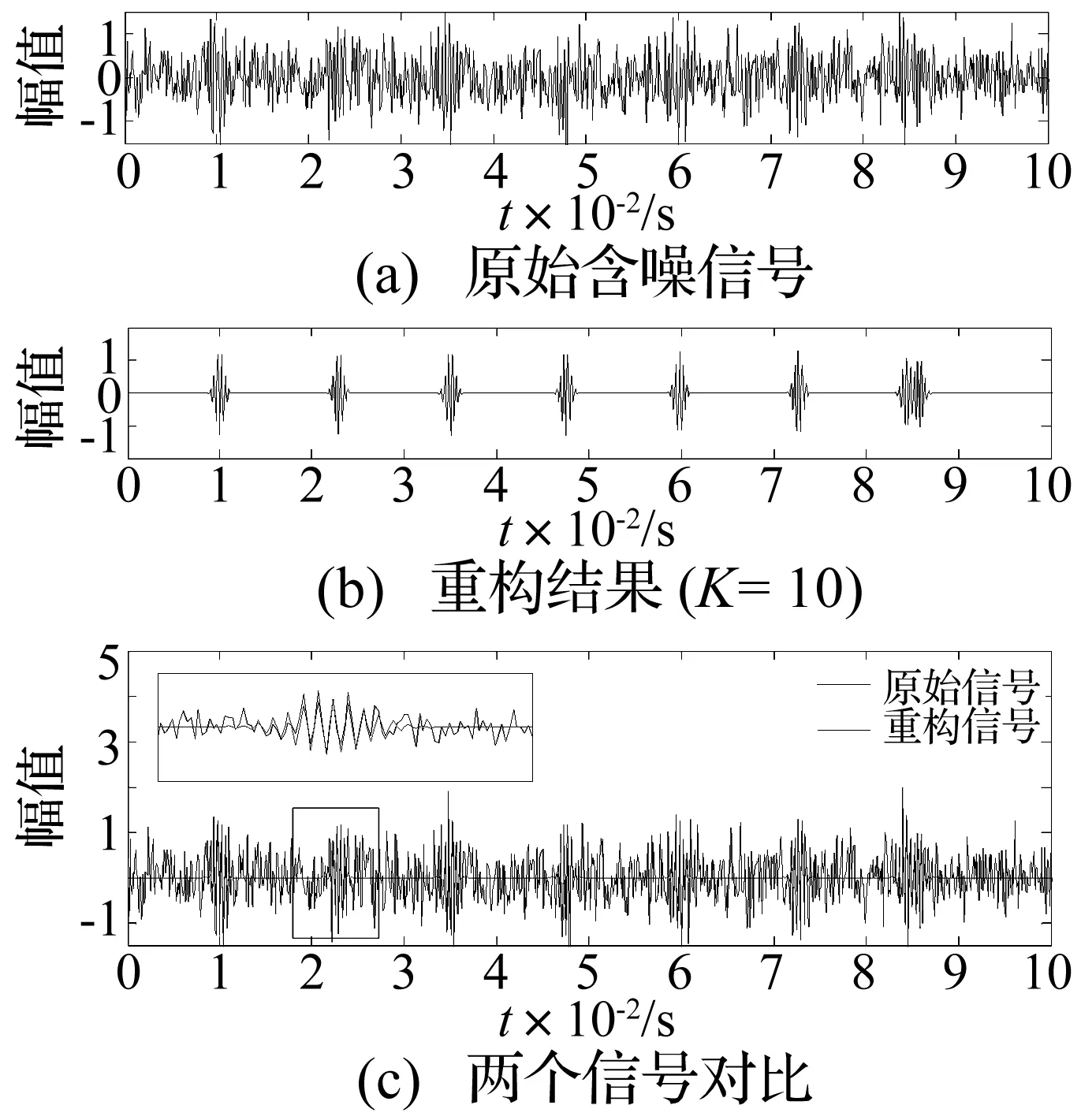
图1 基于时域流形稀疏重构方法的含噪仿真信号结果Fig.1 Results of the TM sparse reconstruction for the simulated noisy signal

图2 不同方法对仿真信号的降噪结果Fig.2 The inner-race defective bearing vibration signal

通过计算VQM，能够定量比较不同方法的去噪效果。计算结果如表1所示，时域流形、MP算法以及时域流形稀疏重构方法都对仿真信号降噪具有效果，但本文方法结果的VQM值最小，即本文方法的降噪能力最强。其他方法去噪能力较差是因为，时域流形方法引起了信号幅值的失真，MP算法的重构过程却不可避免的引入了噪声脉冲。

综上，时域流形稀疏重构方法在故障信号降噪和特征增强方面，比时域流形、MP算法更有效。

表1 不同降噪方法的VQMTab.1 The VQM for the denoising results of the demonstrated simulated signal

3 实例分析

为了验证时域流形稀疏重构方法在实际滚动轴承故障信号中降噪和增强故障特征等方面的有效性，本节分析了具有缺陷故障的轴承内外圈振动信号。实验数据采用美国凯斯西储大学(Case Western Reserve University, CWRU)轴承数据，采样频率为12 000 Hz。测试对象是型号为6205-2RSJEM SKF的深沟球轴承，对测试轴承的内外圈分别采用电火花加工出单故障作为故障源，故障大小为0.011×0.014 inch。本文将转速为1 749 r/min，理论故障频率fd为104.5 Hz的外圈信号以及转速为1 772 r/min，理论故障频率fd为160 Hz的内圈信号作为分析对象。

3.1 时域流形稀疏重构的结果

首先，我们分析滚动轴承外圈故障信号。图3(a)中缺陷轴承外圈信号受到了明显的噪声污染，故障脉冲几乎不能被辨别，图3(b)中时频分布显示在故障频带内和频带外均布满大量噪声，图3(c)包络谱中fd为对应故障频率，2fd是其2倍频。

图3 有缺陷的轴承外圈振动信号Fig.3 The outer-race defective bearing vibration signal

图4 基于时域流形稀疏重构的轴承外圈故障信号分析结果Fig.4 Analyzed result of the outer-race defective bearing signal based on TM sparse reconstruction

使用时域流形稀疏重构的方法，对外圈信号进行处理。图4(a)中本文方法结果的时域信号显示出明显的规则的故障脉冲。图4(b)是基于本方法重构信号的时频分布，可见时频特征非常清晰。图4(c)显示了采用本文方法重构信号的包络谱，噪声明显减少，故障频率突出，fd、2fd分别对应故障频率和其2倍频。

之后，我们分析滚动轴承内圈故障信号。图5(a)中轴承内圈信号噪声较多，故障脉冲信号难以清晰识别，图5(b)中故障信息时频面内分布的大量噪声使得故障脉冲特征不明显，图5(c)是信号的包络谱，fd为对应故障频率，2fd是其2倍频。

图5 有缺陷的轴承内圈振动信号Fig.5 The inner-race defective bearing vibration signal

采用时域流形稀疏重构的方法处理故障轴承内圈信号。图6(a)中重构后的时域波形故障脉冲明显规则。图6(b)在重构后信号的时频分布中故障脉冲特征变得十分清晰。图6(c)本文方法重构信号的包络谱显示，噪声得到抑制，故障特征明显增强，fd为故障频率，2fd为其2倍频。

图6 基于时域流形稀疏重构的轴承内圈故障信号分析结果Fig.6 Analyzed result of the inner-race defective bearing signal based on TM sparse reconstruction

综上，对轴承内外圈局部缺陷的振动信号使用时域流形稀疏重构的方法处理，能够结合TM和MP方法的优点，在保持幅值信息的条件下，消除噪声，清晰地提取出正确数量的故障特征脉冲，且与原信号的幅值匹配良好。说明该方法是一种有效的抑制信号噪声增强故障特征的信号重构方法。

3.2 和其他方法的对比

时域流形稀疏重构方法结合了TM和MP两种方法的优点，这里将以上分析结果与TM和MP的结果进行对比。

从原子选取的角度比较时域流形稀疏重构方法和MP算法。图7为轴承内外圈故障信号分别在MP算法和时域流形稀疏重构方法中的迭代残值能量变化曲线。图中可直接观察到本文方法残值能量下降的很快，且在相同ε的条件下，本文方法分解重构原信号需要的原子数目明显少于MP算法。这些均说明本文方法在选取原子表达信号时效率更高，相比较MP算法，能够更有效地避免冗余原子对噪声的过度表达。

图7 轴承故障信号TM稀疏重构和MP方法迭代残值能量变化Fig.7 Changes of iteration residual energy of the defective bearing signals by TM sparse reconstruction and MP methods

从最终处理结果来比较时域流形稀疏重构方法和TM、MP方法。对于滚动轴承外圈故障信号，图8(a)、图8(b)中时域流形稀疏重构的结果，消除了大部分噪声，清晰地提取到故障脉冲。图8(c)、图8(d)中虽然TM方法抑制了噪声，但故障特征没有本文方法得到的结果明显，而且时频谱中脉冲形状畸变，同时TM的结果幅值信息不正确。图8(e)、图8(f)中MP也能够消除噪声提取故障脉冲，但是MP方法重构信号时对噪声过度表达致使提取到一些伪脉冲，使得故障特征不明显。故在滚动轴承外圈故障信号的分析中，时域流形稀疏重构方法比TM和MP方法都更加有效。

(a) 时域流形稀疏重构的结果(b) 时域流形稀疏重构结果的时频分布

(c) TM的结果(d) TM结果的时频分布

(e) MP的结果(g) MP结果的时频分布图8 不同方法分析轴承外圈故障信号的结果Fig.8Resultsoftheouter-racedefectivebearingsignalbydifferentmethods

对于滚动轴承内圈故障信号，图9显示了时域流形稀疏重构方法与TM、MP方法的对比结果。图9(a)、图9(b)中采用时域流形稀疏重构方法，噪声有明显的抑制，故障脉冲特征明显增强。图9(c)、图9(d)中TM方法抑制了噪声，但故障脉冲特征没有本文方法清晰，且时频谱上脉冲发生畸变，同时TM结果幅值信息严重失真。图9(e)、图9(f)中MP算法也能够消除噪声提取故障脉冲， 其对噪声信号的过度表达致使其

(a) 故障信号(b)故障信号的时频分布

(c) 时域流形稀疏重构的结果(d) 时域流形稀疏重构结果的时频分布

(e) TM的结果(f) TM结果的时频分布图9 不同方法分析轴承内圈故障信号的结果Fig.9Resultsoftheinner-racedefectivebearingsignalbydifferentmethods

得到的故障特征没有本文方法明显。故在轴承内圈故障信号分析中，也显示了时域流形稀疏重构方法比TM、MP方法具有更好的效果。

4 结 论

本文针对轴承故障信号降噪和故障特征增强问题，提出了时域流形稀疏重构的理论分析方法。所提出的方法利用了TM和MP两者的优点，克服了两者的不足，具有两个明显的优点：①时域流形稀疏重构利用了时域流形对应非平稳信号中本质的动力学结构特征，能够把隐含在轴承故障信号中的故障特征有效提取出来，具有显著的噪声抑制效果，一定程度上避免了稀疏重构过程中对噪声过度表达的问题；②时域流形稀疏重构利用匹配追踪的方法重构信号克服了时域流形学习非线性处理带来的幅值信息失真问题，保持了信号的幅值信息，并利用稀疏的特性增强了故障特征。针对实验轴承数据中内外圈故障信号的实例分析，时域流形稀疏重构方法获得了良好的结果，显示了该方法相比TM和MP分析方法的优越性。

[1] LI R, HE D. Rotational machine health monitoring and fault detection using EMD-based acoustic emission feature quantification[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(4): 990-1001.

[2] HE Q, LIU Y, KONG F. Machine fault signature analysis by midpoint-based empirical mode decomposition[J]. Measurement Science and Technology, 2011, 22(1): 15702-15712.

[3] DAPONTE P, FAZIO G, MOLINARO A. Detection of echoes using time-frequency analysis techniques[J]. IEEE Transactions on Instrumentation and Measurement, 1996,45(1): 30-40.

[4] SHIN Y J, POWERS E J, CHOE T S, et al. Application of time-frequency domain reflectometry for detection and localization of a fault on a coaxial cable[J]. IEEE Transactions on Instrumentation and Measurement, 2005, 54(6): 2493-2500.

[5] AHRON M, ELAD M, BRUCKSTEIN A M. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Instrumentation and Measurement, 2006, 15(11): 4311-4322.

[6] CUI L, WANG J, LEE S C. Matching pursuit of an adaptive impulse dictionary for bearing fault diagnosis[J]. Journal of Sound and Vibration 2014, 333: 2840-2862.

[7] MA J. Improved iterative curvelet thresholding for compressed sensing and measurement[J]. Instrumentation and Measurement, IEEE Transactions on, 2016,60 (1):126-136.

[8] MALLAT S, ZHANG Z. Matching pursuit with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12):3397-3415.

[9] LIU B, LING S, GRIBONVAL R. Bearing failure detection using matching pursuit[J]. NDT & E International, 2002, 35(4):255-262.

[10] GELLE G, COLAS M, DELAUNAY G. Blind sources separation applied to rotating machines monitoring by acoustical and vibrations analysis[J]. Mechanical Systems Signal Processing, 2000, 14(3):427-442.

[11] COIFMAN R R, WICKERHAUSER M V. Entropy-based algorithms for best basis selection[J]. IEEE Transactions on Information Theory, 1992,38: 713-718.

[12] CHEN S S, DONOHO D L, SAUNDERS M A. Atomic decomposition by basis pursuit[J]. SIAM Review,2001,43(1):129-159.

[13] 阳建宏,徐金梧,杨德斌,等. 基于主流形识别的非线性时间序列降噪方法及在故障诊断中的应用[J].机械工程学报,2006,42(8):154-158. YANG Jianhong, XU Jinwu, YANG Debin, et al. Noise reduction method for nonlinear time series based on principal manifold learning and its application to fault diagnosis[J]. Chinese Journal of Mechanical Engineering, 2006, 42(8):154-158.

[14] HE Q, LIU Y, LONG Q, et al. Time-frequency manifold as a signature for machine health diagnosis[J]. Instrumentation and Measurement, IEEE Transactions on,2012,61(5):1218-1230.

[15] HE Q, WANG X, ZHOU Q. Vibration sensor data denoising using a time-frequency manifold for machinery fault diagnosis[J]. Sensors, 2014,14:382-402.

[16] HE Q. Time-frequency manifold for nonlinear feature extraction in machinery fault diagnosis[J]. Mechanical Systems and Signal Processing,2013,35(2):200-218.

[17] 何清波,丁晓喜,王俊. 旋转机械故障时频流形诊断分析研究[J].振动与冲击,2014,33(增刊1):302-304. HE Qingbo, DING Xiaoxi, WANG Jun. Rotating machine fault diagnosis by time-frequency manifold analysis[J]. Journal of Vibration and Shock,2014,33(Sup1):302-304.

[18] ZHANG Z Y, ZHA H Y. Principal manifolds and nonlinear dimensionality reduction via tangent space alignment[J]. Journal of Shanghai University, 2005, 8(4):406-424.

[19] 杨庆,陈桂明,江良洲,等. 带标志点的LTSA算法及其在轴承故障诊断中的应用[J].振动工程学报,2012,25(6):732-738. YANG Qing, CHEN Guiming, JIANG Liangzhou, et al. Local tangent space alignment algorithm based on selecting landmark points and its application in fault diagnosis for rolling bearing[J]. Journal of Vibration Engineering,2012,25(6):732-738.

[20] 栗茂林, 王孙安, 梁霖. 利用非线性流形学习的轴承早期故障特征提取方法[J]. 西安交通大学学报,2010,44(5):45-49. LI Maolin, WANG Sun’an, LIANG Lin. Feature extraction for incipient fault diagnosis of rolling bearings based on nonlinear manifold learning[J]. Journal of Xi’an Jiaotong University,2010,44(5):45-49.

[21] 孙斌, 刘立远, 牛翀. 基于局部切空间排列和K-最近邻分类器的转子故障诊断方法[J].中国机械工程,2015,26(1):74-78. SUN Bin, LIU Liyuan, NIU Chong. Rotor fault diagnosis methods based on local tangent space alignment and K-nearest neighbor[J]. China Mechanical Engineering,2015,26(1):74-78.

Rolling element bearing fault signature enhancement based on a time-domain manifold sparse reconstruction method

ZHANG Wenqing1,2， HE Qingbo1， DING Xiaoxi1， HAN Jie2，XIE Mingwei2

(1. Department of Precision Machinery and Precision Instrumentation, University of Science and Technology of China, Hefei 230026, China;2. Facility Design and Instrumentation Institute, China Aerodynamic Research and Development Center, Mianyang 621000, China)

Vibration signal denoising has been one of the most important tasks in signal processing for rolling element bearing fault diagnosis. This paper proposed a new method named time-domain manifold sparse reconstruction method by combining the advantages of time-domain manifold (TM) and matching pursuit (MP). The TM shows the merits of noise suppression and fault information enhancement but it cannot maintain the amplitude information of the signal due to its nonlinear processing. The ability of denoising for the MP is related to the atom itself. Because of the inability to ensure that the selected atoms are the most suitable, the ability of the noise reduction is limited. The proposed method overcomed these problems. Firstly, we found the most appropriate atoms from an overcomplete dictionary based on the TM result by the MP method. Secondly, we computed the coefficients from the atoms and the origianl signal. Finally, we reconstructed the signal by the atoms and the coefficients achieved before. The proposed method has been employed to deal with defective bearing signals to verify the effectiveness. The results show that the new method is superior to the TM and the MP.

time-domain manifold; matching pursuit;sparse reconstruction; rolling element bearing fault diagnosis

新世纪优秀人才支持计划资助(NCET-13-0539)

2015-06-25 修改稿收到日期：2015-10-30

张文清 男，研究生，助理工程师，1990年生

何清波 男，博士，副教授，1980年生 E-mail：qbhe@ustc.edu.cn

TH17; TP277

A

10.13465/j.cnki.jvs.2016.24.030