南海中尺度涡边缘亚中尺度过程模式研究❋
2017-01-06冀承振叶瑞杰董济海张志伟田纪伟
冀承振, 叶瑞杰, 董济海, 张志伟, 田纪伟
(中国海洋大学物理海洋实验室,山东 青岛 266100)
南海中尺度涡边缘亚中尺度过程模式研究❋
冀承振, 叶瑞杰, 董济海❋❋, 张志伟, 田纪伟
(中国海洋大学物理海洋实验室,山东 青岛 266100)
基于高分辨率ROMS模式数据,对南海中尺度涡边缘的亚中尺度过程进行了研究。结果表明:在中尺度涡边缘处存在明显的温度细丝结构,涡度值要明显大于1,O~W参数趋于正值,即在涡旋边缘存在强速度剪切,加强了涡丝的形成。对亚中尺度过程动能空间分布分析发现,中尺度涡边缘区域动能所占的比例大约为88.4%,比中心区域动能所占的比例11.6%要大许多。从动能谱的分析来看,在中尺度涡边缘处动能谱的斜率趋近于k-2,与表层准地转理论(SQG)相吻合,而在中心处呈现k-3,与准地转理论(QG)相一致。
亚中尺度过程;中尺度涡;动能谱;ROMS模式
在现在海洋研究中,人们对中尺度过程(~100km)已有了深入的认识,中尺度过程主要是以中尺度涡旋的形式存在,其水平尺度有几百公里,携带了海洋中大部分能量,通过卫星高度计等观测手段,人们已经对其动力机制及其对水平热量、动量和物质输运的贡献有了很好的理解;同样,人们对尺度小于1km(0.1~100m)的三维湍流过程,及其对海洋混合和能量耗散的作用也做了大量细致的研究[1]。然而,处于中间状态的亚中尺度过程(时间尺度为1 d,空间尺度为1~10km),由于观测资料和数值模拟的限制,往往被人们忽视。实际上,亚中尺度过程往往以亚中尺度涡旋,涡丝,锋面等形式广泛存在上层海洋中[1-8]。在亚中尺度过程发生区域,相对涡度ζ与行星涡度f相当,甚至有时候大于行星涡度f,人们基于罗斯贝数Ro=ζ/f~O(1)来定义亚中尺度过程[1]。
相对于中尺度涡和湍流混合观测而言,亚中尺度过程这一关系到从中尺度过程到小尺度混合之间的过渡阶段的观测工作甚少,其主要原因是:(1)亚中尺度过程水平特征尺度小,目前高度计分辨率过低难以有效监测到;(2)亚中尺度过程时间寿命短,难以有效捕捉到它的生成、传播与消亡过程;(3)亚中尺度过程的生成源具有一定的“随机性”,难以有效开展现场断面观测;(4)尽管亚中尺度过程垂向运动较强,但垂向速度仍在O(mm/s)量级内,对测流仪器的精度要求非常高,目前常规海流观测仪器的精度难以满足。
亚中尺度过程的研究是目前物理海洋研究的前沿之一,其对海洋环流的整体运行机制以及海洋能量的收支平衡有很重要的意义。本文将基于高分辨率(空间分辨率为1km)ROMS模式数据对中尺度涡边缘亚中尺度过程进行研究。
1 模式数据介绍
本文中的ROMS模式使用了单向离线嵌套的方法,对南海北部的亚中尺度过程进行模拟[11]。大区海域范围为15°N~25°N,110°E~126°E,水平分辨率为5 km,该区域模型命名为R5(见图1,黑色实框);嵌套的小区区域范围为18°N~23°N,115°E~121°E,水平分辨率为1 km,该区域模型命名为R1(见图2,蓝色实框)。地形数据使用的是由NOAA提供的分辨率为2′的ETOPO2数据,两个模型在垂向上分层一致,均分为30层,在表层和底部都进行了适当的加密处理。湍流封闭模型本文选择了Generic Length Scale(GLS)模型[12],而边界条件则使用的是放射性边界条件[13]。对于R5模型,其强迫场数据来自于欧洲中期天气预报中心(ECMWF)月平均资料,水平分辨率为0.125°,而开边界条件数据则是来自于HYCOM的月平均资料。为消除不同模式之间的误差,同时获得R5稳定的初始场,先以HYCOM以及ECMWF的气候态数据作为初始、边界以及强迫条件,对R5模型模拟了30年。此时,根据动能和势能随时间的变化曲线可以发现,模式结果已基本稳定。然后,再以得到的稳定结果为初始条件,以HYCOM以及ECMWF的2004—2012年的月平均资料为边界以及强迫条件,对R5模型进行了模拟。在得到R5模型结果之后,再以其作为初始及边界
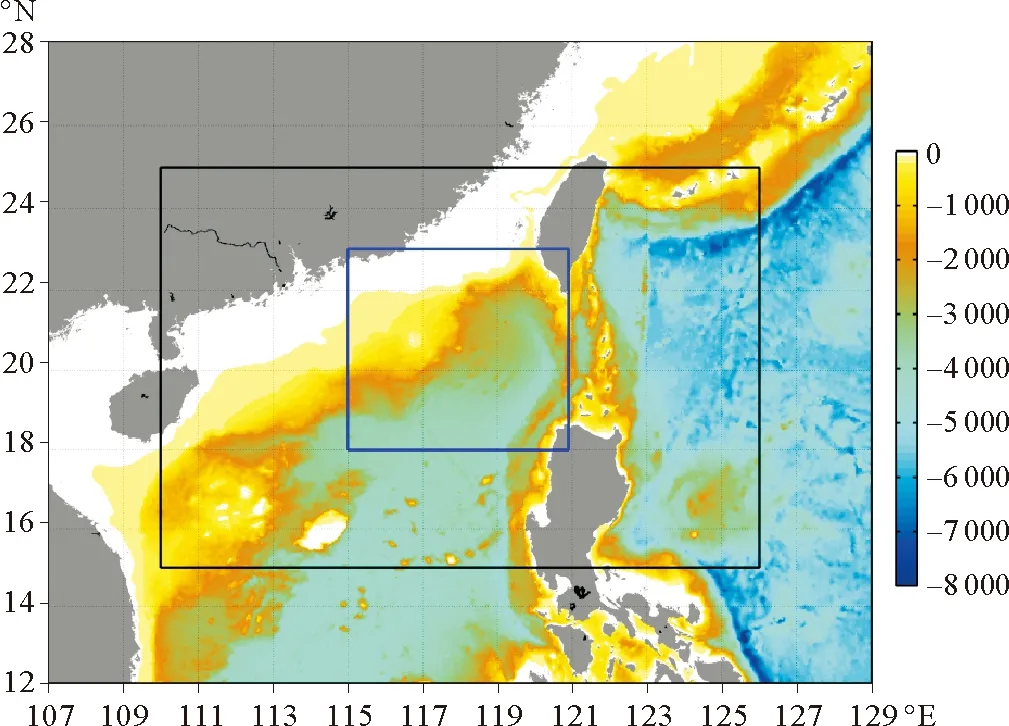
(颜色代表水深。The contour represents water depth.)
条件,以ECMWF的2008—2012年的月平均资料为强迫条件,对R1模型进行了模拟,最终得到R1模型高分辨率的模拟结果。在分析的过程中,我们主要选取了模式稳定后有中尺度涡存在的流场进行分析,以来研究中尺度涡边缘亚中尺度的特征。
2 数值模拟结果分析
2.1 温盐场、涡度场分布
本文选取了2009年12月第19天的模拟结果,从海表面高度(SSH,见图2(a))的结果来看,在南海北部存在一个较强的暖涡,涡中心大致位于118°E,21°N,涡旋半径大约为60km;从海表面温度(SST,见图2(b))可以看出明显的中尺度涡结构,并且在中尺度涡边缘处有明显的温度细丝结构。本文取图2(a)中的黑色实线位置的断面(“118断面”)来分析穿越中尺度涡中心温度和密度的分布。图3给出了沿断面的温度和位势密度的分布,从断面温度的分布来看,最高温度可以达26℃,出现在涡中心的位置,边缘处的温度要低于中心的温度,由于中尺度涡中心存在下凹的缘故,存在明显的等温线下降,在中尺度涡边缘时,混合层底的深度为50m左右,由于中心下凹,混合层底被下压到100m左右的深度上,从位势密度的水平分布上可以看到存在明显的等密度线露头,上混合层中保持了一定的水平浮力梯度。以上的分析表明,中尺度涡自身的特性支持了海洋上混合层中水平浮力梯度的存在,储存了有效位能,正是由于上混合层存在的这种不稳定,为亚中尺度过程的形成创造了潜在的条件[14]。
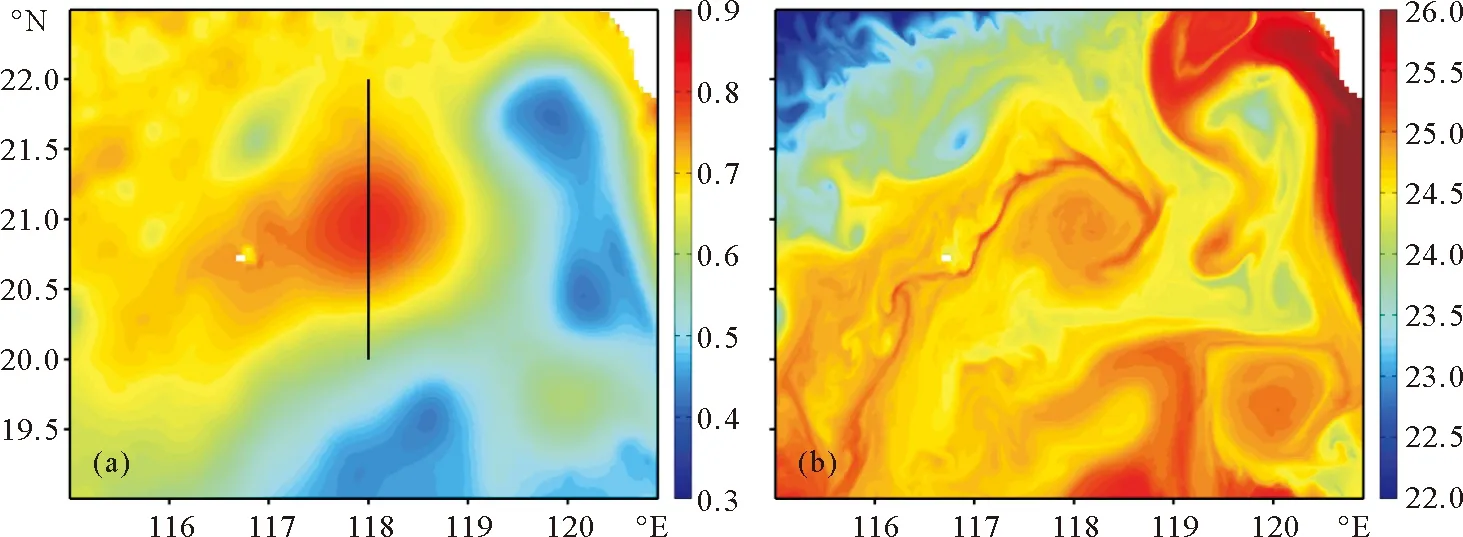
((a)中的黑色实线为选取的“118断面”位置。The black line in (a) is “118 section” that we choose.)
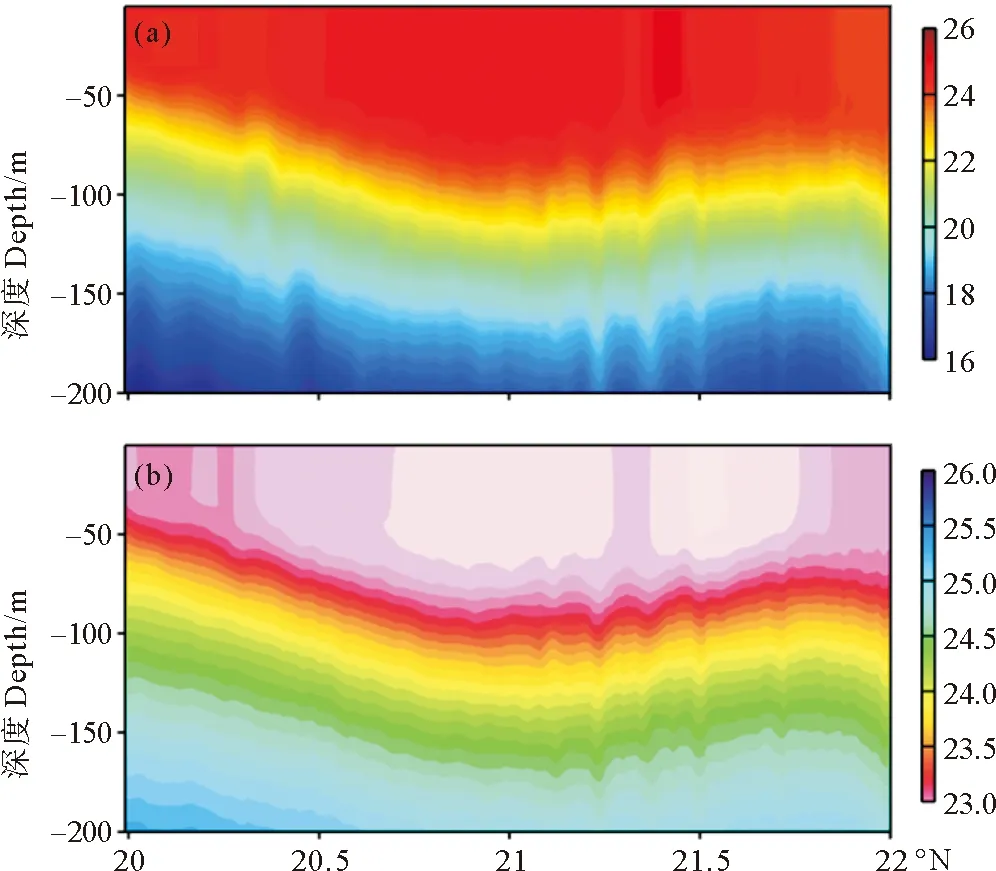
图3 沿118断面的温度分布(单位:℃) (a)及沿118断面的位势密度分布(b)(单位:kg/m3)
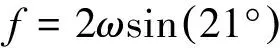
倘若能将我们的设想与现实结合,将会吸引来大批高校学生的向往,在互联网时代,什么都很便利了,人们的生活质量提高,对于服务的追求越来越高,只有以客户为中心,才能为我们引来更多的人流量,进而才能实现共赢,客户得到了美的体验,商家得到了利益。然而在这过程中,应当对商家进行严格的要求,切勿追捧蝇头小利,而送走了客户。
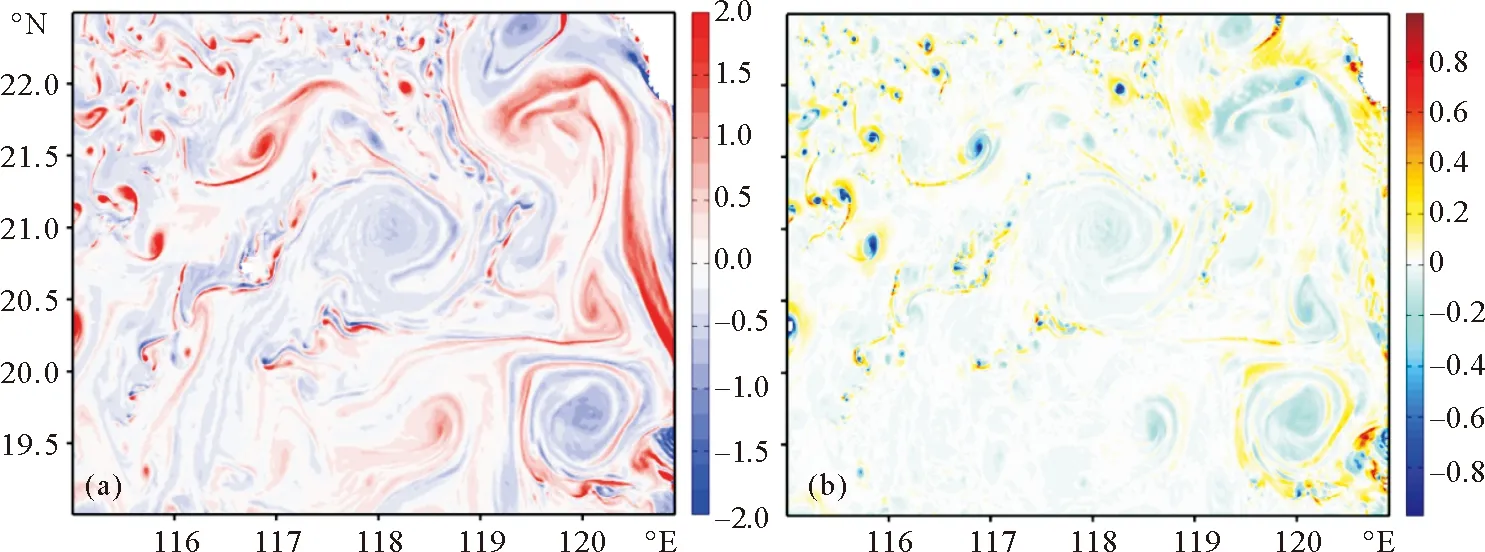
图4 相对涡度的分布(单位: 10-4 s-1) (a)和Okubo-Weiss 参数计算结果及分布 (Unit:10-8s-1) (b)
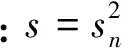
2.2 动能空间分布
图5(a)表示水平流速的u的断面分布,向东为正,由于是一个暖涡,表现为顺时针旋转,因此在21°N以南,u<0,在21°N以北,u>0。最大流速约0.8m·s-1,发生在中尺度涡边缘的表层20m处。相对于水平流速u来说,流速v要小的多,最大流速仅0.15m·s-1。
图6给出了归一化的动能空间分布,本文利用Butter滤波的方法将原始流速分解为中尺度波段(MP,尺度大于20km)和亚中尺度波段(SP,尺度小于20km),对于中尺度波段来说,动能的两个峰值分别出现在20.4°N以及21.4°N附近,处于中尺度涡边缘向中尺度涡内部转化的区域,因为这个区域内流速出现最大值,因此动能较大;相对于中尺度波段的动能来说,亚中尺度波段动能分布大大不同,动能的峰值主要集中于中尺度涡的两个边缘,通过计算,两个边缘区域动能所占的比例分别为26.5%和61.9%,比中心区域动能所占的比例11.6%要大许多。亚中尺度波段动能的分布表明亚中尺度过程在中尺度涡边缘处较为活跃,而在中尺度涡内部则较为“安静”。

图5 水平流速u的断面分布(a)和水平流速v的断面分布(b)(单位:m·s-1)
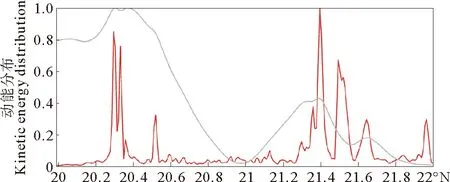
(红线代表亚中尺度波段的动能分布,灰线代表中尺度波段的动能分布。纵坐标经过了各波段最大值归一化处理。The red line and the gray line represent the kinetic energy distribution of SP and MP, respectively and the kinetic energy is normalized by the maximum value of SP and MP, respectively.)
图6 从表层到200m深度动能垂向积分分布图
Fig.6 Depth mean distribution of kinetic energy from top layer to 200m
2.3 动能谱分析
从上面的分析可以得出初步的结论,亚中尺度过程在中尺度涡边缘时要比中尺度涡内部更强一些。作为一种有效的手段,许多高分辨率的数值模式利用动能谱来描述亚中尺度过程[16-20]。在海洋中,处于亚中尺度波段的强非地转流可以从平衡态中获取能量,然后传输给小尺度,准地转二维中尺度过程动能谱特征是斜率为k-3,而高分辨率的能够分辨亚中尺度过程的数值模式发现,谱的斜率变的平缓,变为k-2,受这一启发,本文这一小节从动能谱的角度来分析。
本文在模式中选取了一条穿过中尺度涡中心的断面(118断面,见图2(a)),通过对断面流速的动能谱分析,来探究中尺度涡中心和边缘的差异。根据图6(a)水平流速的分布,作者把穿越中尺度涡中心的118断面分为三个部分,RR1,RR2和RR3,其中RR1的区域范围为20°N~20.7°N,RR2区域范围为20.7°N~21.4°N,RR3区域范围为21.4°N~22.1°N,RR1和RR3代表中尺度涡的边缘区域,RR2则代表中尺度涡的中心区域。
图7给出了RR1,RR2和RR3 3个区域不同深度上的水平流速u的动能谱分析。从图7(a)中可以看出,在RR1区域50、100和150m 3个不同深度上,水平流速波数谱的斜率都接近于k-2,通过线性拟合,可以得到在尺度5~20km的亚中尺度波段,50m处的波数谱斜率为-2.17,100m处为-2.30,150m处为-2.34,说明亚中尺度过程到150m处还比较强;在RR3处也有相类似的结果(见图7c),在5~20km的亚中尺度波段,50,100和150m处的波数谱斜率分别为-2.15,-2.27,-2.24,斜率随深度的变化更接近于k-2;但在RR2处,情况有所不同(见图7(b)),50,100和150m的波数谱斜率分别为-2.81,-2.82,-2.91,比RR1和RR3区域的波数谱斜率要陡一些,斜率随深度的变化更接近于k-3。
从以上的分析可以得出,中尺度涡边缘动能谱的斜率更接近于k-2,比较符合表层准地转理论(SQG理论),而在中尺度涡内部,动能谱的斜率更接近于k-3,与二维准地转理论的预测相一致。Callies[19]及Rocha[21]等在文章中综述了内潮等也有可能使动能谱的斜率变缓,接近于k-2。由于在本文的模式模拟中没有加入潮的作用,因此,本文分析所得到的在中尺度涡边缘处斜率平缓接近于k-2的结果,排除了内潮因素的干扰,即中尺度涡边缘动能谱斜率呈现k-2变化是由于存在丰富的亚中尺度过程导致的。
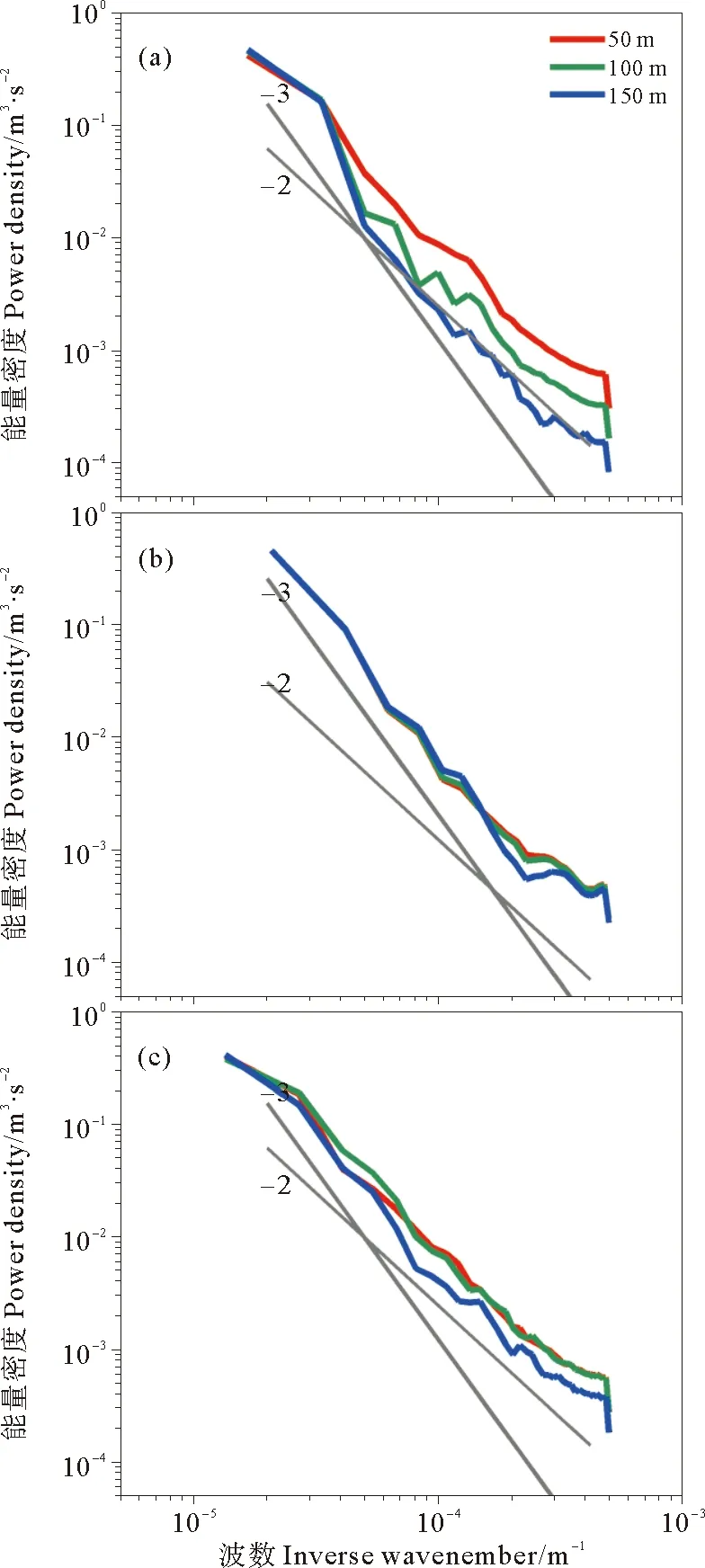
(其中k-2和k-3通过两条灰色直线标出。k2andk-3are warkod by the two grey line.)
图7 中尺度涡边缘RR1处50,100和150m处水平流速的波数谱分析(a);同子图(a),但为中尺度涡中心RR2处的结果(b)及同子图(a),但为中尺度涡边缘RR3的结果(c)
Fig.7 At the edge of the mesoscale eddy (RR1), wavenumber spectra for horizontal velocity at 50 (red line),100 (green line) and 150m (blue line)(a),similar to (a) but at RR2 (b) and similar to (a) but at RR3 (c)
3 结语
本文利用高分辨率ROMS模式数据对南海中尺度涡边缘亚中尺度过程进行研究,温度场的结构显示中尺度涡边缘处有明显的温度细丝结构;上混合层存在水平浮力梯度,导致混合层不稳定,为亚中尺度过程的产生奠定了基础;在中尺度涡边缘处,正负涡度值交错,且其值要明显大于1,O-W参数在涡边缘处趋于正值,表明涡边缘区域的水平流场切变很强,强速度剪切加强了涡丝的形成;动能的空间分布表明中尺度涡边缘区域动能所占的比例大约为88.4%,比中心区域动能所占的比例11.6%要大许多;从动能谱的分析来看,在中尺度涡边缘处动能谱的斜率趋近于k-2,与表层准地转理论(SQG)相吻合,而在中心处呈现k-3,与准地转理论(QG)相一致,由于在模式模拟中没有加入潮的作用,因此排除了内潮因素的干扰,即中尺度涡边缘动能谱斜率呈现k-2变化是由于存在丰富的亚中尺度过程导致的。以上只是模式结果的初步探讨,在下一步工作中,需要对亚中尺度过程产生及消亡机制进一步的研究。
[1] Thomas L N, Tandon A, Mahadevan A. Submesoscale processes and dynamics[J]. Ocean modeling in an Eddying Regime, 2008: 17-38.
[2] Mahadevan A, Tandon A. An analysis of mechanisms for submesoscale vertical motion at ocean fronts[J]. Ocean Modelling, 2006, 14(3): 241-256.
[3] Capet X, McWilliams J C, Molemaker M J, et al. Mesoscale to submesoscale transition in the California Current System. Part I: Flow structure, eddy flux, and observational tests[J]. Journal of Physical Oceanography, 2008, 38(1): 29-43.
[4] Capet X, McWilliams J C, Molemaker M J, et al. Mesoscale to submesoscale transition in the California Current System. Part II: Frontal processes[J]. Journal of Physical Oceanography, 2008, 38(1): 44-64.
[5] Capet X, McWilliams J C, Molemaker M J, et al. Mesoscale to submesoscale transition in the California current system. Part III: Energy balance and flux[J]. Journal of Physical Oceanography, 2008, 38(10): 2256-2269.
[6] Gildor H, Fredj E, Steinbuck J, et al. Evidence for submesoscale barriers to horizontal mixing in the ocean from current measurements and aerial photographs[J]. Journal of Physical Oceanography, 2009, 39(8): 1975-1983.
[7] Klein P, Lapeyre G. The oceanic vertical pump induced by mesoscale and submesoscaleturbulence[J]. Annual Review of Marine Science, 2009, 1: 351-375.
[8] Zhong Y. Submesoscale dynamics and transport properties in the Gulf of Mexico [J].Georgia Insititute of Technology, 2013:121-128.
[9] Lévy M, Iovino D, Resplandy L, et al. Large-scale impacts of submesoscale dynamics on phytoplankton: Local and remote effects[J]. Ocean Modelling, 2012, 43: 77-93.
[10] McGillicuddy D J, Anderson L A, Bates N R, et al. Eddy/wind interactions stimulate extraordinary mid-ocean plankton blooms[J]. Science, 2007, 316(5827): 1021-1026.
[11] Mason E, Molemaker J, Shchepetkin A F, et al. Procedures for offline grid nesting in regional ocean models[J]. Ocean Modelling, 2010, 35(1): 1-15.
[12] Umlauf L, Burchard H. A generic length-scale equation for geophysical turbulence models[J]. Journal of Marine Research, 2003, 61(2): 235-265.
[13] Orlanski I. A simple boundary condition for unbounded hyperbolic flows[J]. Journal of Computational Physics, 1976, 21(3): 251-269.
[14] Boccaletti G, Ferrari R, Fox-Kemper B. Mixed layer instabilities and restratification[J]. Journal of Physical Oceanography, 2007, 37(9): 2228-2250.
[15] Isern-Fontanet J, Font J, García-Ladona E, et al. Spatial structure of anticyclonic eddies in the Algerian basin (Mediterranean Sea) analyzed using the Okubo-Weiss parameter[J]. Deep Sea Research Part II: Topical Studies in Oceanography, 2004, 51(25): 3009-3028.
[16] Capet X, Campos E J, Paiva A M. Submesoscale activity over the Argentinian shelf[J]. Geophysical Research Letters, 2008, 35(15): 2015-2024.
[17] Wang D P, Flagg C N, Donohue K, et al. Wavenumber spectrum in the Gulf Stream from shipboard ADCP observations and comparison with altimetry measurements[J]. Journal of Physical Oceanography, 2010, 40(4): 840-844.
[18] Qiu B, Chen S, Klein P, et al. Seasonal mesoscale and submesoscale eddy variability along the North Pacific Subtropical Countercurrent[J]. Journal of Physical Oceanography, 2014, 44(12): 3079-3098.
[19] Callies J, Ferrari R. Interpreting energy and tracer spectra of upper-ocean turbulence in the submesoscale range (1-200km)[J]. Journal of Physical Oceanography, 2013, 43(11): 2456-2474.
[20] Callies J, Ferrari R, Klymak J M, et al. Seasonality in submesoscaleturbulence[J]. Nature Communications, 2015, 6.
[21] Rocha C B, Chereskin T K, Gille S T, et al. Mesoscale to submesoscale wavenumber spectra in Drake Passage[J]. Journal of Physical Oceanography, 2015, 46: 601-620.
责任编辑 庞 旻
The Simulation of Submesoscale Processat the Periphery of a Mesoscale Eddy in the South China Sea
JI Cheng-Zhen, YE Rui-Jie, DONG Ji-Hai, ZHANG Zhi-Wei, Tian Ji-Wei
(Physical Oceanography Lab, Ocean University of China, Qingdao 266100, China)
The study investigates thesubmesoscale process at a mesoscale eddy in South China Sea (SCS) based on high-resolution ROMS model. The results show that, at the periphery of themesoscale eddy,there exists obvious temperature filaments, the vorticity value is significantly greater than 1, andO-Wparameter tends to be positive, all of these evidences meanthat the shear of velocity is much stronger and strengthen the formation of vortex filaments. From the view ofkinetic energy’s distribution, for submesoscale process, the proportion at the periphery of the eddy (RR1 and RR3) is 88.4%, which is larger than that at the center (RR2,only 11.6%).The results of kinetic energy spectra indicate that the slope of the spectra at the periphery of the eddy holdsk-2regime, which is more likely with surface quasi-geostrophic (SQG), while the slope exhibitsk-3law at the eddy’s center, consistent with quasi-geostrophic (QG) theory.
submesoscale process; mesoscale eddy; kinetic energy spectra; ROMS model
国家重点基础研究发展计划项目(2014CB745003) 资助 Supported by the National Key Basic Research and Development Program of China(2014CB745003)
2016-03-13;
2016-05-06
冀承振(1990-),男,硕士生。E-mail:jichengzhen@126.com
❋❋ 通讯作者:E-mail:jihaihappy@163.com
P722.7
A
1672-5174(2017)01-001-06
10.16441/j.cnki.hdxb.20160068
冀承振, 叶瑞杰, 董济海, 等. 南海中尺度涡边缘亚中尺度过程模式研究[J]. 中国海洋大学学报(自然科学版), 2017, 47(1): 1-6.
JI Cheng-Zhen, YE Rui-Jie, DONG Ji-Hai, et al. The simulation of submesoscale processat the periphery of a mesoscale eddy in the South China Sea[J]. Periodical of Ocean University of China, 2017, 47(1): 1-6.
