基于POF的温度应力加速试验失效机理一致性研究

（中国航天标准化与产品保证研究院，北京 100071）

基于POF的温度应力加速试验失效机理一致性研究

郑志腾，董澍，徐丹君，蔡健平，伍招冲

（中国航天标准化与产品保证研究院，北京 100071）

目的通过失效物理手段得到温度加速寿命试验的失效机理突变点，节省试验样本，并为加速寿命试验的有效性提供保障。方法利用电子产品典型失效物理模型，在求解MOSFET器件激活能的基础上确定失效机理突变点，并开展失效物理分析，从微观分析的角度验证失效机理一致性判定方法的理论正确性和工程适用性。结果MOSFET器件在温度低于240 ℃时，失效机理没有发生改变；温度高于240 ℃时，失效机理发生了改变，与前述失效机理不一致。结论基于失效物理的方法可以确定器件机理发生变化的温度应力点，所需样本量小。

加速试验；失效物理；失效机理一致性

加速试验是在保证失效机理不变的前提下，提高试验应力水平，使产品加速失效，以便在短时间内获得失效数据，从而评估产品正常应力水平下的可靠性或寿命指标[1—3]。然而，由于加速条件下试验应力水平高，产品潜在的失效机理可能被激发出来，成为主要失效机理，从而使得加速条件下失效机理发生改变，导致由加速试验获得的器件寿命不能代表器件的真实寿命，造成无效加速时间，产生巨大的浪费，所以进行加速试验失效机理的一致性判定是非常有必要的。

目前，国内外判定电子类产品加速试验失效机理一致性的方法一般是基于统计的传统验证方法，开展验证工作需要大量的样本，往往不能满足航天产品小子样的需求。失效物理（POF，Physics of Failure）方法以产品失效为核心，关注产品的失效机理或失效的根本原因，强调对失效的物理、化学过程的定量分析和描述，为长寿命、高可靠、小样本航天电子产品加速试验失效机理一致性验证提供了新的技术途径[4—6]。文中在借鉴已有电子产品典型失效机理和失效物理模型的基础上，提出了基于失效物理分析的温度加速试验失效机理一致性判别方法，并选取星上二次电源中的关键功率器件——MOSFET管为典型产品开展工程验证，为小子样、高可靠航天电子产品温度加速试验的有效性提供技术保证。

1 加速模型分类

研究加速试验失效机理一致性，首先要了解加速模型及其物理意义，才能使失效机理一致性判定更具有针对性。加速模型按其提出时基于的方法可以分为三类，即物理加速模型、经验加速模型和统计加速模型[7—14]，如图1所示。

图1 加速模型分类Fig.1 The classification for accelerated model

物理加速模型是基于对产品失效过程的物理化学解释而提出的。典型的物理加速模型有Arrhenius模型和艾林模型等，描述了产品寿命和温度应力之间的关系。经验加速模型是基于工程师对产品寿命受应力影响的长期观察总结而提出的，如线性累积损伤模型、Coffin-Manson模型等。统计加速模型是基于统计方法给出的，又可分为参数模型和非参数模型。由于三种类型的加速模型中只有物理加速模型是基于产品失效的物理、化学而建立的加速模型，所以文中基于失效物理的加速试验失效机理一致性研究方法只适用于物理加速模型。

2 基于POF的失效机理温度突变点确定

2.1 电子产品温度失效物理模型及工程验证研究

2.1.1 失效物理理论模型研究

根据文献[4]和文献[5]，电子器件在温度应力作用下发生退化是由器件表面和内部金属化系统发生物理化学变化引起的，其主要失效机理为电迁移、热载流子注入和介质击穿三种，影响其失效的主要参数为电流、电压、温度等，可以得到描述产品在温度应力下失效时间的统一物理模型：

式中：tf为失效前时间；A0为与材料/工艺相关的系数；n为电流幂指数；m为电压幂指数；T为试验中器件的结温；Ea为失效激活能；kB为波尔兹曼常数。

由于失效时间与退化率为逆关系，则器件的退化速率与施加在器件上的加速应力所满足的关系为：

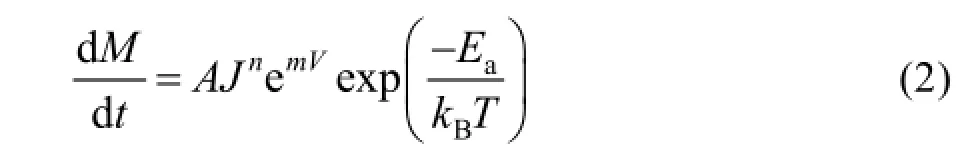
式中：A为常数；M为失效敏感参数；dM/dt为器件失效敏感参数退化速率。

对于电子产品，一般选用温度应力进行加速寿命试验，对器件施加按一定速率β上升的环境温度应力，则t时刻器件的结温可以表示为[15]：

式中：T0为初始温度；β为升温速率；ΔT为器件加电后由焦耳热产生的自升温[16]。由式（3）可得：

将式（4）代入式（2）可得：

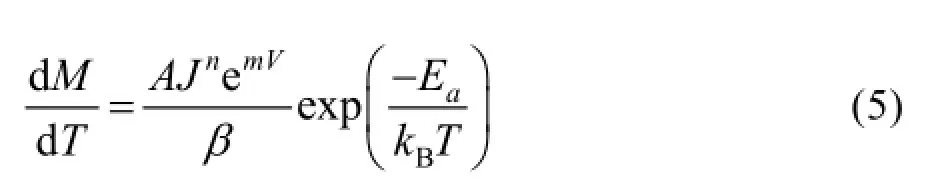
对式（5）在某一温度段1T到2T内进行积分，可得：

即

其中2TMΔ 和1TMΔ 分别为2T和1T温度下对应的敏感参数有效退化量。

对式（7）在另一段时间3T到4T内积分，可得：

式（7）和（8）两式相比，可得：

式(9）中，只有Ea为未知量，从而可在失效机理一致性的范围内计算失效激活能。若在某一温度段内计算出的激活能发生了改变，则可认为器件的失效机理发生了改变，即可得出失效机理保持一致的温度范围，以及失效机理发生改变的温度点。

2.1.2 工程验证

选取某型星上二次电源关键功率器件 N沟道MOSFET管，设计并开展温度试验，测量MOSFET管的失效敏感参数—阈值电压Vth随温度的变化数值，如图2所示。可以看出，随着温度应力的不断增大，此MOSFET器件的阈值电压Vth不断减小，呈稳定下降趋势。

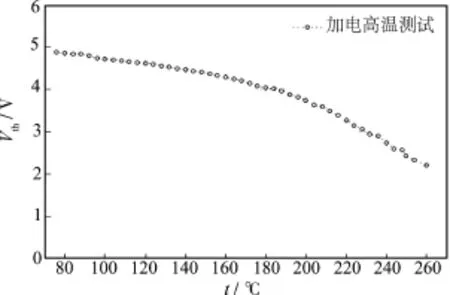
图2 不同温度下阈值电压数据Fig.2 The threshhold voltage at different temperature

根据失效物理模型公式（9）求得各个温度下对应的激活能数据如图3所示，激活能在整个试验温度内表现为三段区域，在拐点处失效机理发生了改变，失效机理发生改变的温度约为240 ℃。在失效机理发生改变的区域和未改变的区域存在一个警告区域，经过计算区域的值为224～236 ℃。在设计加速寿命试验时，应尽量避开此区域，以保证加速试验的有效性。

图3 不同温度下激活能数据Fig.3 The activation energy at different temperature

2.2 MOSFET器件失效物理分析研究

2.2.1 加速寿命试验实施

由以上分析可知，MOSFET器件的失效机理在240 ℃左右发生了改变。为了更好地验证失效物理模型求解的正确性，结合失效物理分析手段开展失效机理突变点的研究。选取4个MOSFET器件，分别在180，200，220，240 ℃条件下开展恒温加速寿命试验，待产品失效后，进行失效物理分析工作。

为了避免温度升高过快对MOSFET器件可能造成的意外影响，试验开始时，应缓慢升高温度，50 ℃温度应力下保持24 h。根据GJB 150.3A，以＜3 /min℃ 的升温速率将温度升高至相应的温度（底板温度）。考虑到高温下产品输出参数可能出现温度漂移，产品失效判据定为：输出参数超出产品达到稳定状态后输出参数量值的35%范围。最后对四个不同温度应力下的样品开展失效物理分析，研究其失效机理的差异性。

2.2.2 失效物理分析研究

试验后失效样品如图4所示。

对不同温度下的样品用等离子刻蚀方法开封后的样品进行低倍扫描分析，其形貌如图5所示。可以看出，180，200，220 ℃三个温度应力下，样品的芯片与基体贴合较为紧密，240 ℃温度下的样品的芯片与基体发生了脱落现象。

图4 试验失效样品Fig.4 Thefailure samplee s

图5 不同温度应力下失效样品低倍微观形貌Fig.5 The SEEM morphologgy of failure saamples at different tempperature

由电-热耦合仿真分析（如图6所示）可知，MOOSFET器件承受应力量级的最高点为芯片和键合引线的连接处，所以对芯片和键合引线处进行高倍显微镜扫描分析，对比不同温度下表面微观形貌的差异性，从而研究不同温度下失效机理的异同。

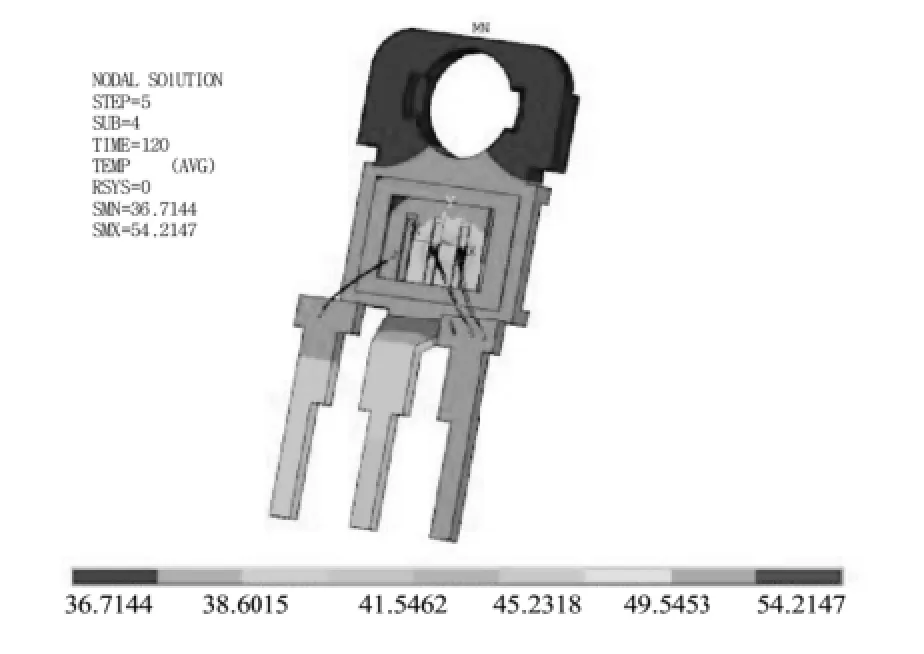
图6 电-热耦合仿真应力分布FF ig.6 The strr ess distributioon of electricaland thermal coupling simulation

芯片和键合引线的高倍形貌如图77所示，可以看出180，200，220 ℃三个温度应力下，样品的键合引线处较为平滑，240 ℃温度下的样品键合引线处由圆球形的颗粒状物质（图7c箭头所示）。由于温度过高，导致键合引线处的元素发生氧化反应，从而形成了白色颗粒状物质，导致失效机理发生了改变。

对四个样品进行成分分析，取三种主要元素Ag，Cu，O的含量进行测试，得到界面元素含量见表1。可以看出，随着温度的升高，界面中Ag，Cu元素的含量不断升高，说明在加电状态下，由于温度的作用使得Ag，Cu等金属元素向界面发生了迁移，使得其含量越来越高。180，200，220 ℃三个温度应力下，界面中O元素含量为微量，240 ℃条件下O元素含量升高，说明界面的金属元素发生了氧化作用，从而导致失效机理的突变。

表1 不同温度下主要元素质量分数Table 1 Content analysis for main elements at different temperature

综上所述，通过失效物理分析，可以验证器件在240 ℃失效机理发生变化的原因，也证实了基于物理模型求解激活能方法的正确性。基于失效物理的失效机理一致性验证方法的求解和分析过程较为复杂，但只需较少的样本量就可以求解失效机理发生变化的温度应力点，对于小子样航天产品开展加速寿命试验设计具有切实的工程意义。

3 结论

利用失效物理方法得到了电子器件温度应力的失效机理突变点，得到如下结论。

1）通过温度应力物理加速模型求解激活能，若激活能在某一温度范围内发生了变化，失效机理随之发生改变。文中所选航天MOSFET器件的失效机理发生改变的温度为240 ℃左右，在设计加速寿命试验时，应力水平应小于此温度，以保证加速试验的有效性。

2）对不同温度条件下失效后的样品进行失效物理分析，240 ℃时器件键合引线处的形貌和元素含量发生变化，由于高温作用使得失效机理发生了改变，也验证了模型求解激活能判定失效机理一致性的合理性。

3）在推导得到电子产品失效物理模型的基础上，只需测试一个MOSFET器件的失效敏感参数随时间的变化规律即可求得不同温度下的激活能，从而进行失效机理突变点的判定，达到节省试验样本的目的。

[1] 姜同敏, 王晓红, 袁宏杰, 等. 可靠性试验技术[J]. 北京: 北京航空航天大学出版社, 2012: 185. JIANG Tong-min, WANG Xiao-hong, YUAN Hong-jie, et al. Reliability Test Technology[J]. Beijing: Beihang University Press, 2012: 185.

[2] 陈循, 张春华. 加速试验技术的研究、应用与发展[J]. 机械工程学报, 2009(8): 130—136. CHEN Xun, ZHANG Chun-hua. Research, Application and Development of Accelerated Testing[J]. Journal of Mechanical Engineering, 2009(8): 130—136.

[3] 王召斌, 任万滨, 翟国富. 加速退化试验与加速寿命试验技术综述[J]. 低压电器, 2010(9): 1—6. WANG Zhao-bin, REN Wan-bin, ZHAI Guo-fu. Review of Accelerated Degradation Testing and Accelerated Life Testing[J]. Low Voltage Apparatus, 2010(9): 1—6.

[4] 郭春生, 万宁, 马卫东, 等. 恒定温度应力加速实验失效机理一致性快速判别方法[J]. 物理学报, 2013(17): 17—22. GUO Chun-sheng, WAN Ning, MA Wei-dong, et al. Rapid Identification Method of the Consistency of Failure Mechanism in Constant Temperature Stress Accelerated Testing[J]. Acta Phys, 2013(17): 17—22.

[5] 郭春生, 谢雪松, 马卫东. 快速评价半导体器件失效激活能的方法[J]. 半导体技术, 2006 (2): 122—126. GUO Chun-sheng, XIE Xue-song, MA Wei-dong. Rapid Evaluation Method of Activation Energy for Semiconductor Device[J]. Semiconductor Technology, 2006(2): 122—126.

[6] 麦克弗森 J W. 可靠性物理与工程—失效时间模型[M].北京: 科学出版社, 2013: 56—78. MF J W. Reliability Physics and Engineering: Time-to-Failure Moldeling[M]. Beijing: Science Press, 2013: 56—78.

[7] KIM Jung-woo, YOON Dongcheol, JEON Minseok, et al. Degradation Behaviors and Failure Analysis of Ni-BaTi03 Base-metal Electrode Multilayer Ceramic Capacitors under Highly Accelerated Life Test[J]. Current Applied Physics, 2010(3): 157—158.

[8] 陈文霞, 谢文殊, 曾声奎. 功能分析与失效物理结合的可靠性预计方法[J]. 航空学报, 2008(5): 1133—1138. CHEN Wen-xia, XIE Wen-shu, ZENG Sheng-kui. Functional Analysis and Physics of Failure Associated Reliability Prediction[J]. Acta Aeronautica Et Astronautica Sinica, 2008(5): 1133—1138.

[9] 马甜, 李传日, 程祺, 等. 基于失效物理的微波组件贮存寿命加速试验及预测[J]. 装备环境工程, 2013, 10(4):30—33. MA Tian, LI Chuan-ri, CHENG Qi, et al. Microwave Components Accelerated Life Test and PredictionBased on the Failure Physics[J]. Equipment Environment Engineering, 2013, 10(4): 30—33.

[10] 范志峰, 齐杏林, 雷彬. 加速可靠性试验综述[J]. 装备环境工程, 2008, 5(2): 37—39. FAN Zhi-feng, QI Xing-lin, LEI Bin. Review of AcceleratedReliabilityTests[J]. Equipment Environment Engineering, 2008, 5(2): 37—39.

[11] 黄婷婷, 姜同敏. 加速寿命试验中统计加速模型综述[J].装备环境工程, 2010, 7(4): 57—62. HUANG Ting-ting, JIANG Tong-min. Review of Statistical Acceleration Models in Accelerated Life Testing[J]. Equipment Environment Engineering, 2010, 7(4): 57—62.

[12] 魏高乐, 陈志军. 基于多应力综合加速模型的产品可靠性评估方法[J]. 科学技术与工程, 2016(2): 24—29. WEI Gao-le, CHEN Zhi-jun. A Product Reliability Evaluation Method Based on Multi-stress Comprehensive Acceleration Model[J]. Science Technology and Engineering, 2016(2): 24—29.

[13] 李海波, 张正平, 胡彦平. 加速寿命试验方法及其在航天产品中的应用[J] .强度与环境, 2007, 34(1): 2—10. LI Hai-bo, ZHANG Zheng-ping, HU Yan-ping. Accelerated Life Testing Method and Its Applications for Space Products[J]. Structure& Environment Engineering, 2007, 34(1): 2—10.

[14] 张秋菊, 刘承禹. 电子设备可靠性的加速试验[J]. 光电技 术应用, 2011 (4): 81—85. ZHANG Qiu-ju, LIU Cheng-yu. Reliability Accelerated Testing(RAT)for Electronic Equipments[J]. Electro-optic Technology Opplication, 2011(4): 81—85.

[15] JIANG S T. Assessment of Semi-parametric Proportional Intensity Model Aliped to Recurrent Failure Data with Multiple Failure Types For Repairable System Reliability[D]. Norman: University of Oklahoma, 2014.

[16] ARZU O, PADGETTB W J. A Penalized Local D-optimality Approach to Design for Accelerated Test Models[J]. Journal of Statistical Planning and Inference, 2004, 119(2): 411—420.

Failure Mechanism Consistency of Accelerated Test for POF Based Temperature Stress

ZHENG Zhi-teng, DONG Shu, XU Dan-jun, CAI Jian-ping, WU Zhao-chong
(China Academy of Aerospace Standardization and Product Assurance, Beijing 100071, China)

ObjectiveTo save test sample and provide guarantee for efficiency of accelerated test by obtaining change point of failure mechanism in the POF-based accelerated life test.MethodsTypical physical model of failure was applied to determine the change point of failure mechanism based on calculating the activation energy of MOSFET. And failure physical analysis was implemented to verify the theoretical correctness and engineering applicability of judgment method on consistency of failure mechanism from the micro perspective.ResultsWhen temperature was below 240 ℃ , the failure mechanism did not change. And when the temperature was higher than 240 ℃ , the failure mechanism changed. It was inconsistent with the above mentioned failure mechanism.ConclusionThe POF method can confirm the temperature stress point of changed device mechanism and the required sample size is small.

accelerated life test; POF; consistency of failure mechanism

10.7643/ issn.1672-9242.2016.06.018

TN306

A

1672-9242(2016)06-0104-06

2016-07-09；

2016-08-05

Received：2016-07-09；Revised：2016-08-05

“十二五”科工局技术基础科研项目(Z032014B001)

Fund：Suported by the "Twelfth Five-Year" Technology Basic Research Project. State Administration of Science, Technology, and Industry for National Defence(Z032014B001)

郑志腾（1986—）,男，硕士，工程师, 主要从事航天产品可靠性试验、评估等方面的研究。

Biography：ZHENG Zhi-teng (1986—), Male, Master, Engineer, Research focus:reliability test and assessment of aerospace products.