关注个性，在高中数学课堂中实现因材施教

江苏省常熟市浒浦高级中学 杨广娟

关注个性，在高中数学课堂中实现因材施教

江苏省常熟市浒浦高级中学 杨广娟

在高中数学教学当中，每一个学生都是独立的个体，从知识现状到理解能力方面都存在着诸多差异。有效的教学活动应当关注并适用于每个学生，这便要求教师们在设计教学时需要允许多种可能性的存在，让不同学习特点的学生都能够从中找到适合自己的落脚点。这也就是我们将要在本文当中探讨的因材施教的课题。因材施教并不是某个特定时间点所需要的教学策略，它是贯穿于整个教学过程始终的。因此，于数学教学开展的各个阶段，都应当对因材施教的理念加以渗透。

一、从学生特点出发，于分组环节因材施教

从本质上来讲，因材施教就是分层教学的一种表现形式。因此，以小组作为教学开展的基本形式，也是十分常用的教学设计途径。既然每个学生都具有自己的个性特点，那么，在将学生进行分组时，教师们便应当将这种特点作为合理分组的重要参考依据，有区分、有结合地构建起更利于高效教学的模式。

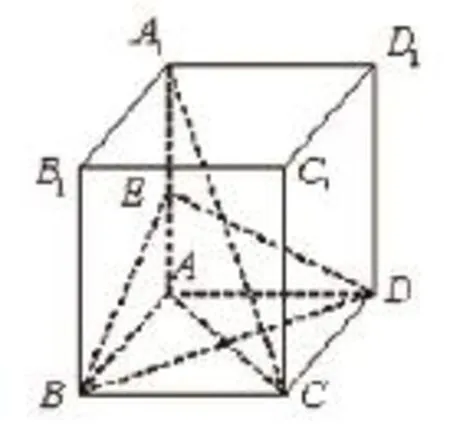
例如，在立体几何知识学习中，学生所具备的能力差异是比较显著的。于是，我将擅长作图、擅长空间想象与擅长定理推导的学生分布在每个小组中，并请小组完成如下问题解答：在正方体ABCDA1B1C1D1中，E是AA1的中点，求证：（1）A1C∥面BDE。（2）面AA1C⊥面BDE。这样一来，具有上述不同特长的学生可以分工合作，分别完成画图（如图）、分析线面位置与推导求证的工作。很快地，问题就得到了顺利解决，大家还对利用三角形中位线判定线面平行有了深入理解。

根据学生特点进行分组时，大体上可以从两种原则进行把握：一是集中分组，也就是将学习能力相近的学生分为一组，使小组内学生之间的学习节奏能够保持近似一致，整体效率更高；二是穿插分组，就是在同一个小组中交叉分配不同学习能力与特长的学生，实现能力互补。根据具体教学内容的需要，教师们可以灵活适用上述原则，均能得到较好的效果。

二、从目标设定出发，在课堂环节因材施教

高效优质的课堂教学离不开科学合理的目标设定。教学目标对于整个教学活动的开展来讲，起到了一个方向性的指引作用。因此，教师们在实际教学过程当中，不要急于呈现具体知识内容，而是要先将目标确定好。既然学生们的知识基础与接受能力不尽相同，其所能够达成的学习效果自然也有所差异。教学目标的设定便应当反映出这一点。

例如，在对函数单调性的内容进行教学设计时，我将初次课堂教学的目标确立为两个：一是能够运用函数单调性特点确定最值，二是能够根据单调区间确定函数解析式。两个目标之间呈现出难度递增的趋势，自然也就能够被不同知识能力的学生所选择。基本知识教授完成后，我依照上述教学目标，为学生们设计了如下练习题：已知函数f（x）=x2+2ax+2，x∈[-5,5]。（1）当a=-1时，求函数的最大值和最小值。（2）求实数a的取值范围，使y=f（x）在区间[-5,5]上是单调函数。在个性化教学目标的指引之下，上述问题设置方式也为学生们提供了分别接受的平台。

因材施教设定教学目标，对于教师和学生来讲都是很有好处的。对于教师来讲，将教学目标进行划分的过程本身就是在对教学活动加以细化。这样一来，教师可以根据不同的教学目标来重点关注相应学生的学习效果，更加直接，也更具针对性。而对于学生来讲，以阶梯状态存在的教学目标，更利于他们找到自己能够接受的着陆点，既能大大减轻心理压力，也可更加集中精力开展学习。

三、从总结提炼出发，在点评环节因材施教

只顾学习而没有总结，是低效率的数学学习。特别是对于高中阶段数量巨大的知识内容来讲，如果没有及时有效地提炼总结，学生们必然无法将之全面到位地掌握。作为教学效果提升的关键环节，教师们在总结提炼过程当中也是应当将因材施教的理念加以渗透的。

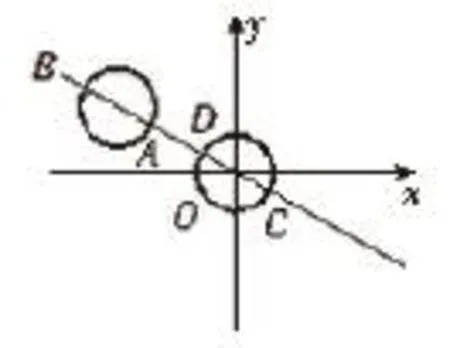
例如，在三角函数的教学过程中，学生们遇到了这样一个问题：求y=（cosθ-cosα+3）2+（sinθ-sinα-2）2的最大（小）值。最为理想的方法就是将y值看作求两动点P（cosθ,sinθ）与Q（cosα-3,sinα+2）之间距离的最值问题，然后通过将两动点的轨迹方程x2+y2=1和（x+3）2+（y-2）2=1转化为求两曲线上两点之间距离的最值问题（如图）顺利求解。在点评中，我从具体解题思路和同类题目解答的规律方法两个层面进行了分析。对于知识基础比较薄弱的学生来讲，应当从已知条件中意识到其与圆的方程之间的相似形态，进而确立思维方向。而对于知识能力较强的学生来讲，则应当站在更高的视角，从中总结出数形结合的思想方法，并将其运用到更多类似问题的解答当中去。

几乎在每一次课堂教学的末尾，笔者都会进行点评，不仅是要对学生们本次学习的表现加以肯定与指正，更是为了对知识当中存在的典型思想方法进行总结提炼，带领学生们的思维走向升华。相对于具体知识内容的学习来讲，这显然是一个较高层次的要求，学生之间必然会出现不同的接受效果。因此，教师们在就此进行点评时，也应当合理划定层次，为学生提供多角度的接受可能。

通过前文当中的论述不难发现，因材施教的教学方式开展的前提基础是教师对于学生个性差异的关注。我们在这里所说的个性，并非是从性格角度来讲的，而是指每个学生个体之间的学习能力差异。教师们只有把握住了学生们的个性之所在，才能相应设计出适合于各种能力状态学生的教学方式与要求，将高中数学教学的每个动作落到实处。本文所阐述的只是较有代表性的几种情况，还有更多的创新路径等待广大教师们去发现和开拓。