一种确定模糊数决策矩阵属性权重的方法

成亚丽

(成都工业学院 信息与计算科学系，成都 611730)

一种确定模糊数决策矩阵属性权重的方法

成亚丽*

(成都工业学院 信息与计算科学系，成都 611730)

在实际的多属性决策过程中，往往由于决策自身的模糊和不确定因素，从而导致了方案的属性值、属性权系数等等参数的不确定和不完备。针对关于属性权重未知且属性值为三角模糊数的多属性决策问题，利用属性的熵计算出属性权重，三角模糊数排序进行比较，进而从备选方案中选出最优方案。实例分析说明，该方法在实际应用中是可行有效的。

多属性决策；三角模糊数；熵；权重

1965年，美国加利福尼亚大学专家Zadeth LA发表了一篇开创性论文“Fuzzy Sets”，标志着模糊数学的诞生[1]。其中熵的概念是由德国物理学家克劳修斯于1865年提出的，最开始它是产生于热力学，主要被用来描述运动过程中的一种不可逆现象，之后信息论之父C.E.Shannon将其加以推广应用，在信息论中用熵来表示事物出现的不确定性,并提出了计算信息熵的数学表达式。多属性决策是有限方案的选择问题，它的理论及方法已经广泛应用到经济、管理、工程、军事和社会等诸多领域[2]。20多年的发展使得多属性决策问题的研究有了很多成果，但仍面临很多问题[3]。其中，解决多属性决策问题的方法大都需要求解属性权重[4]，由于方案的好坏或者排序与属性权重有着密切的关系，所以如何确定权重是至关重要的。目前主要的求解方法有：1)基于决策者给出偏好信息的方法，比如利用特征向量[5]、最小平方和[6]方法；2)基于决策矩阵信息的方法，比如主成分分析法[7]、多目标最优化法[8-9]和熵法[10]，其中李鹏等[11]利用直觉模糊数的熵得到每个属性的信息熵，从而计算出属性权重。

本文就属性权重未知且属性值为三角模糊数的多属性决策问题，利用属性的信息熵求出属性权重，进而从备选方案中选出最优方案，最后进行了实例分析，说明该方法可行有效。

1 基本概念和性质

定义2[12]设=(a,和B=(b,是2个三角模糊数，令

D(,

(1)

称为三角模糊数的距离公式。显然，当D越大，则三角模糊数数,的距离越远；D=0，两三角函数相等。

定义3 基于优于关系模糊数排序方法[13]，

2 问题的提出及优化模型的构建

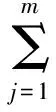
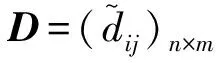
i=1,2,…,n,j=1,2,…,m。

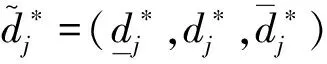
一般的，若决策方案在属性下的属性Uj值差异小的话，则说明该属性对属性决策所起的作用较小；反之，差异大的话，则说明所起的作用较大。因此我们可以得出，方案属性值偏差越大的属性应当赋予越大的权重。由熵的定义概念可以得出，某个属性下的熵值越小，则说明所起作用越大，权重就越大。

由于决策矩阵是三角模糊函数，无法直接利用熵值法，故之前通过属性值与理想属性值的距离公式将决策矩阵进行量化处理。决策矩阵的方案属性值偏差大小与距离矩阵的方案属性值的偏差大小具有一致性，通过比较属性值偏差大小来对方案优劣进行排序。在此基础上，给出具体算法步骤。

步骤1：由定义4确定方案理想属性值；

步骤2：通过式(1)求解属性值与理想属性值的距离公式：

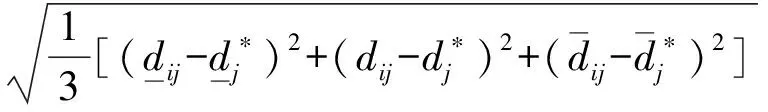
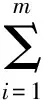
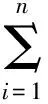
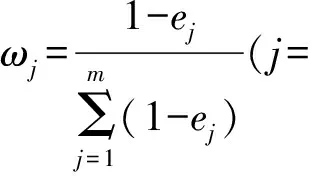
(2)

对其进行排序进而确定最优方案。

3 算例

本文引用文献[16]算例进行实际分析。假设某单位对干部进行考核选拔，根据实际情况要求，制订了6项考核指标(属性)包括：思想品德U1、工作态度U2、工作作风U3、文化程度U4、领导能力U5和开拓能力U6。从中推荐确定了5名候选人Xi(i+1,2,3,4,5)进行考核。已知各属性均是效益型，给出模糊决策矩阵D：

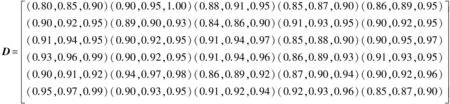
(3)

1)通过步骤1，2将决策矩阵转化为规范化距离矩阵R′：

2)通过步骤3求得熵值：

e1=0.823 1,e2=0.643 5,e3=0.732 5,

e4=0.812 4,e5=0.845 4,e6=0.806 1

属性权重向量为：

w=(0.133 5,0.266 3,0.199 8,0.140 1,0.115 5,0.144 8)T。

3)通过步骤4最后求出方案Yi综合属性值，并对其进行排序得出：X2≻X3≻X5≻X4≻X1。

结果与原文中结果一致。

4 结论

本文针对属性权重未知且属性值为三角模糊数的多属性决策问题，提出了利用属性的熵计算出属性权重，三角模糊数排序进行比较，进而从备选方案中选出最优方案。最后通过进行实例分析，说明该方法在实际应用中是可行有效的。当然本文提出的方法也可以推广到其他类型模糊数决策问题中，可进一步进行研究。

[1] 罗承忠.模糊集引论[M].北京:北京师范大学出版社,1989.

[2] 张市方.几种模糊多属性决策方法及其应用[D]. 西安:西安电子科技大学,2012.

[3] KOELE P.Multiple attribute decision making:an introduction[J].Journal of Behavioral Decision Making,1997,10(2):151.

[4] 姜艳萍,樊治平.三角模糊数互补判断矩阵排序的一种实用方法[J].系统工程,2002,20(2):89-92.

[5] SAATY T L.A scaling method for priorities in hierarchical structures[J].Journal of Mathematical Psychology,1977,15(3):234-281.

[6] CHU A T W.A comparison of two methods for determining the weights of belonging to fuzzy sets[J].Journal of Optimization Theory and Applications,1979,27(4):531-538.

[7] 严鸿和,陈玉祥.专家评分机理与最优综合评价模型[J].系统工程理论与实践,1989(2):19-23.

[8] 王应明,傅国伟.运用无限方案多目标决策方法进行有限方案多目标决策[J].控制与决策,1993(1):25-29.

[9] 樊治平.多属性决策的一种新方法[J].系统工程,1994(1):25-28.

[10] HWANG C L,YOON K.Multiple attribute decision making[M]//Fuzzy Multiple Objective Decision Making:Springer-Verlag,1994:287-288.

[11] 李鹏,魏翠萍.直觉模糊多属性决策的新方法[J].计算机工程与应用,2009,45(1):59-60.

[12] 张市芳.几种模糊多属性决策方法及其应用[D].西安: 西安电子科技大学,2012.

[13] 成亚丽.变量为三角模糊数的规划问题研究[D].成都:西南交通大学,2010.

[14] 王霞.基于三角模糊数特征参数模的多属性决策[J].数学的实践与认识,2013,43(13):289-294.

[15] 朱方霞,陈华友.确定区间数决策矩阵属性权重的方法:熵值法[J].安徽大学学报(自然科学版),2006,30(5):4-6.

[16] 徐泽水.对方案有偏好的三角模糊数型多属性决策方法研究[J].系统工程与电子技术,2002,24(8):9-12.

Methods for Triangular Fuzzy Numbers Multi-attribute Decision Making Problem

CHENGYali*

(Department of Information and Computing Science, Chengdu Technological University, Chengdu 611730, China)

In the course of multiple attribute decision making, due to fuzziness and uncertainty decision-making itself, lead to the scheme of attribute value and attribute weight parameters uncertain and incomplete. Aiming at these problems, In this paper, the attribute weights are unknown and the attribute values for the triangular fuzzy numbers multiple attribute decision making problems, Using the properties of information entropy and attribute weights, of a ranking method of triangular fuzzy numbers, and then choose the optimal solution from alternative. At last, the example analysis show that the method is feasible and effective.

multi-attribute decision-making; triangular fuzzy numbers; entropy; weight

10.13542/j.cnki.51-1747/tn.2016.04.019

2016-11-30

成亚丽(1983— )，女(汉族)，山西晋城人，讲师，硕士研究方向：优化与决策，通信作者邮箱：262121812@qq.com。

C934

A

2095-5383(2016)04-0075-03