求解广义Rosenau-Kawahara-RLW方程的守恒差分算法

卓 茹，黄妗肜，胡劲松

(西华大学 理学院，成都 610039)

求解广义Rosenau-Kawahara-RLW方程的守恒差分算法

卓 茹，黄妗肜，胡劲松*

(西华大学 理学院，成都 610039)

对一类带有齐次边界条件的广义Rosenau-Kawahara-RLW方程进行了数值研究，提出了一个两层非线性有限差分格式，格式合理地模拟了问题的一个守恒性质，得到了差分解的先验估计和存在唯一性，并利用离散泛函分析方法分析了差分格式的二阶收敛性与无条件稳定性。

广义Rosenau-Kawahara-RLW方程；守恒差分格式；收敛性；稳定性

本文考虑如下一类广义Rosenau-Kawahara-RLW方程[1-2]的初边值问题：

u1-αuxxtβuxxxxt+aux+b(up)x+ɛuxxx-λuxxxxx=0，

(x,t)∈(xL,xR)×(0，T]

(1)

u(x,0)=u0(x),x∈[xL,xR]

(2)

u(xL,t)=u(xR,t)=0,ux(xL,t)=ux(xR,t)=0,

uxx(xL,t)=uxx(xR,t)=0,t∈[0,T]

(3)其中：p≥2为整数；α,β,a,b,ε,λ为已知常数，且

α>0,β>0；u0(x)是一个已知的光滑函数。由于方程(1)的渐近边界条件满足：

当 │x│→+∞时，u→0，ux→0，uxx→0,所以当-xL>>0，xR>>0时，初边值问题(1—3)与方程(1)的Cauchy问题是一致的。问题(1—3)满足如下守恒量[2]：

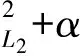
(4)

其中：E(0)均为仅与初始条件有关的常数。

在对紧离散系统的描述中，广义Rosenau-Kawahara-RLW方程(1)是一类重要的非线性发展方程。当α=ε=λ=0时，方程(1)即为著名的广义Rosenau方程[3-4]；当α=β=0时，方程(1)即为广义Kawahara方程[5-7]或四阶KdV方程；当β=ε=λ=0时，方程(1)即为广义RLW方程[8-9]。这些方程在流体力学、等离子物理学等领域有广泛的应用，研究其数值解很有理论价值和应用价值，目前仅有文献[2]对广义Rosenau-Kawahara-RLW方程提出了一个三层线性差分格式。本文对问题(1—3)提出了一个具有二阶精度的两层非线性有限差分格式，该格式合理地模拟了守恒量(4)，并给出了差分解的存在唯一性以及各式的收敛性、稳定性等理论证明。

1 差分格式和守恒律

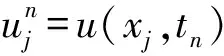
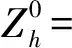
0,j=-2,-1,0,…,J,J+1,J+2}，

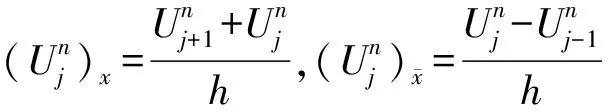
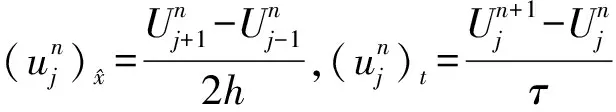
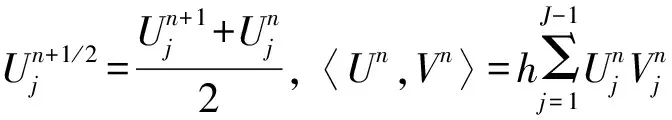
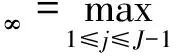
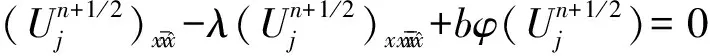
(j=1,2,…,J-1;n=1,2,…,N-1)

(5)

(6)

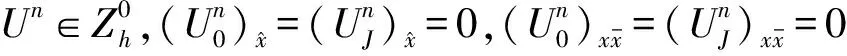
(n=0,1,2,…,N)

(7)

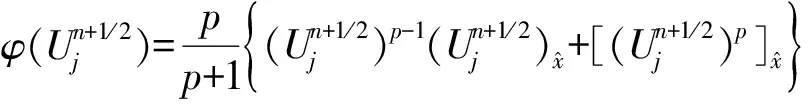
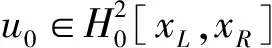
(8)

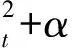
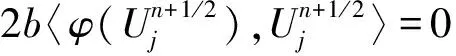
(9)

由边界条件(7)和分部求和公式[10]，得

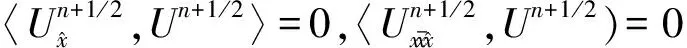
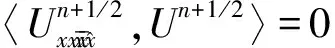
(10)

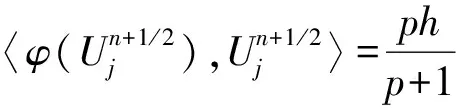
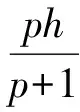
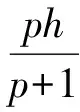
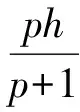
(11)

将式(10)、(11)代入式(9)后，递推即可得式(8)。

2 差分解的存在性

引理1(Brouwer不动点定理[11])设H是有限维的内积空间，设g∶H→H是连续算子且存在一个δ>0使得∀x∈H，‖x‖=δ时有〈g(x),x〉>0，则存在一个x*∈H使得g(x*)=0且‖x*‖=δ。

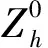
(12)

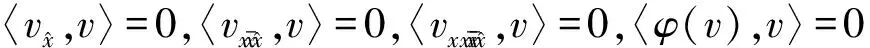
再由Cauchy-Schwarz不等式，得

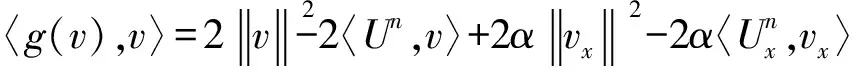
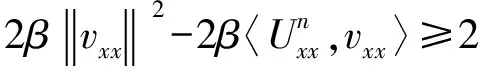
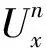
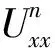
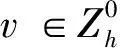
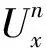
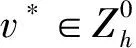
3 差分格式的收敛性与稳定性及其解的唯一性

差分格式(5—7)的截断误差定义如下：

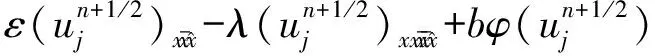
(13)

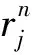
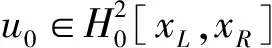
‖u‖L2≤C,‖ux‖L2≤C,‖uxx‖L2≤C,‖u‖L∞≤C,‖ux‖L∞≤C。

证明：由式(4)，有

‖u‖L2≤C,‖ux‖L2≤C,‖uxx‖L2≤C,

最后由Sobolev不等式[11]得：‖u‖L∞≤C，‖ux‖L∞≤C。

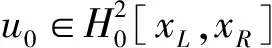
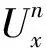
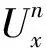
证明：由定理1，有

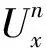
再由离散Sobolev不等式[11]得：

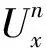
注：定理3表明，差分格式(5—7)的解Un以‖·‖∞无条件稳定。

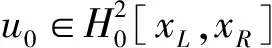
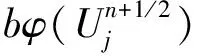
(14)

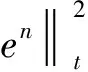
2b〈φ(un+1/2)-φ(Un+1/2),en+1/2〉=

〈rn,2en+1/2〉，

(15)

类似于(10)式，有

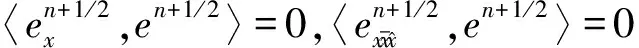
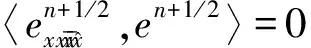
(16)

又由引理2，定理3及Cauchy-Schwarz不等式，有

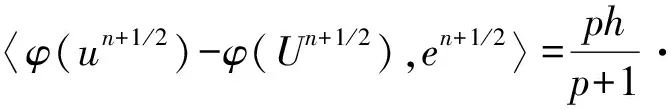
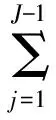
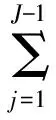
(17)

又〈rn,2en+1/2〉=〈rn,en+1+en〉≤

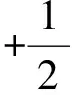
(18)

将式(16—18)代入式(15)，整理有：

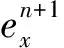
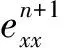
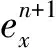
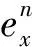
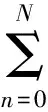
(20)

又B0=O(τ2+h2)2，

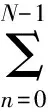
于是(20)式为：

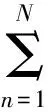
由离散的Gronwall不等式[11]可得

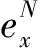
最后由离散Sobolev不等式[11]，有‖eN‖∞≤O(τ2+h2)。

定理5 差分格式(5—7)的解是唯一的。

证明：设Vn是差分格式(5—7)的另外一个解，令，类似于定理4的证明可得：‖‖∞=0，从而有Vn=Un。证毕。

[1] ZUO J M.Soliton solutions of a general Rosenau-Kawahara-RLW equation[J].Bmc Plant Biology,2015,7(2):1-19.

[2] HE D,PAN K.A linearly implicit conservative difference scheme for the generalized Rosenau-Kawahara-RLW equation[J].Applied Mathematics & Computation,2015,271(C):323-336.

[3] SANK K C,AMIYA K P.Numerical methods for the rosenau equation[J].Applicable Analysis,2001,77(3-4):351-369.

[4] FENG B,MIN X C,YU Y Y,et al.A new three level conservative finite difference scheme for the Rosenau equation[J].Sichuan Daxue Xuebao,2011,48(1):7-12.

[5] WAZWAZ A M.New solitary wave solutions to the modified Kawahara equation[J].Physics Letters A,2007, 360(4-5):588-592.

[6] POLAT N,KAYA D,TUTALAR H I.A analytic and numerical solution to a modified Kawahara equation and a convergence analysis of the method[J].Applied Mathematics & Computation,2006,181(179):466-472.

[7] JIN L.Application of variational iteration method and homotopy perturbation method to the modified Kawahara equation[J].Mathematical & Computer Modelling,2009,49(3-4):573-578.

[8] ZHANG L.A finite difference scheme for generalized regularized long-wave equation ☆[J].Applied Mathematics & Computation,2005,168(168):962-972.

[9] 王廷春,张鲁明.求解广义正则长波方程的守恒差分格式[J].应用数学学报,2006,29(6):1091-1098.

[10] ZHOU Y.Application of discrete functional analysis to the finite difference method[J].Fourier,1990,8(1):49-65.

[11] BROWDER F E.Existence and uniqueness theorems for solutions of nonlinear boundary value problems[J].Proc.Sympos.Appl.Math,1965:24-49.

Conservative Difference Scheme for Solving General Rosenau-Kawahara-RLW Equation

ZHUORu,HUANGJinrong,HUJinsong*

(School of Science, Xihua University, Chengdu 610039, China)

In this paper, the numerical solution of initial-boundary value problem for generalized Rosenau-Kawahara-RLW equation with non-homogeneous boundary is considered. A nonlinear two-level difference scheme is designed. The difference schemes can well simulate one conservative quantities of the problem. The priori existence and uniqueness of the finite difference solution are also obtained. It is proved that the finite difference scheme is convergent with second order and unconditional stable by discrete functional analysis method.

general Rosenau-Kawahara-RLW equation; finite difference scheme; convergence; stability

10.13542/j.cnki.51-1747/tn.2016.04.018

2016-09-20

四川省教育厅基金项目“两类波动方程的守恒型数值算法研究”(16ZA0167)；西华大学重点基金项目“某些非线性波动方程的高精度数值方法研究”(Z1513324)

卓茹(1991— )，女(汉族)，四川仁寿人，在读硕士研究生，研究方向：微分方程数值解。 胡劲松(1973— )，男(汉族)，四川射洪人，教授，博士，研究方向：微分方程数值解，通信作者邮箱：hjs888hjs@163.com。

O241.82

A

2095-5383(2016)04-0072-03