一类变时间分数阶扩散方程的Chebyshev小波数值法
2017-01-05韩永杰黄泽霞
许 燕,张 敏,韩永杰,黄泽霞
(1.四川科技职业学院 基础部,成都 611745;2.西华大学 理学院,成都 610039)
一类变时间分数阶扩散方程的Chebyshev小波数值法
许 燕1,张 敏1,韩永杰2*,黄泽霞2
(1.四川科技职业学院 基础部,成都 611745;2.西华大学 理学院,成都 610039)
运用第二类Chebyshev小波函数拟合的方法,求解一类变时间分数阶扩散方程。通过推导得出第二类Chebyshev小波的变阶微分算子矩阵,进而利用算子矩阵将方程转化为一组线性方程组,再利用最小二乘的方法求得方程组的解,进而得到原方程的数值解。并给出数值算例验证了本方法的有效性。
变时间分数阶扩散方程;第二类Chebyshev小波;算子矩阵;数值解
1 引言及预备知识
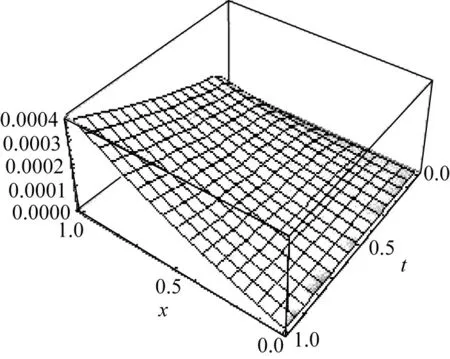
分数阶微积分在自然科学和工程问题的应用中一直以来备受关注,它的一个最大的优势在于其描述各种物理过程时具有历史的记忆性和继承性。近几年大量文献里提出很多分数阶微积分方程的数值解法,Samko等[1]推广了Riemann-Liouvile和Marchaud分数阶微积分到变阶情况,同时推导出一些相应性质和转化公式。Hartley和Lorenzo等[2]提出了变阶算子不但可以是与微积分无关的变量(t)的函数,而且可以还是其他(如空间)变量(y)的函数。Coimbra[3]以Caputo分数阶导数的拉普拉斯变换作为基础,提出了一个新的变阶微分算子的定义;Pedro等[4]利用变阶模型研究了悬挂在一粘性液体中的粒子在受到阻力时的运动。Sum等[5]根据产生变阶数的可能的物理背景引入了一类变分数阶的扩散模型。在很多文献中出现的各种变阶算子定义中,主要有Caputo变阶算子,Marchaud变阶算子,Coimbra变阶算子[2-4]等。但从数值角度看,Coimbra定义的变阶算子更为有效。因此,本文采用Coimbra定义[6]的变阶算子。由于变阶算子中含有一个变阶的指数部分,对求解变分数阶微分方程的解析解带来了很大的困难。因此,很多研究者置身于研究其数值解。Fiu等[7]提出了带非线性源项的变分数阶扩散方程的显式和隐式欧拉方法,并证明了这两种方法数值解的稳定性和收敛性。在文献[8]中提到对变分数阶微分给出了变阶反常次扩散方程的2种高精度数值格式。目前,对于变分数阶微分方程的求解现在很多文献中都只是给出了解析解的差分格式[9-11]。沈淑君[11]首先利用分段线性插值离散时间变分数阶导数,同时利用中心差分离散空间二阶导数,然后采用Richardson外推法改进精度求解Coimbra定义的变时间分数阶微分方程的数值解,此类方程为:
(1)
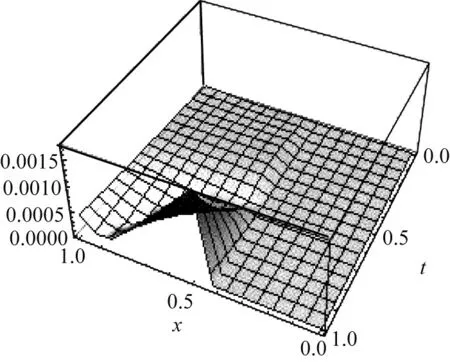
其中:0 定义1 Coimbra定义的变时间分数阶导数 (2) 其中:0 (3) Caputo变阶微分算子有如下性质: 1)线性性质 (4) (5) 为方便描述本文用到的第二类Chebyshev小波定义,首先给出如下的示性函数的定义: 定义2 示性函数I{A}(x)是定义在实数上的一元分段函数 其中:B是一个给定的实数集合,在不致引起混淆的情况下也将其记为I{x∈B}或I{B}。 本文为了推导的简便将采用如下形式的选择函数: (6) 其中:x∈R,k,n=1,2,…。 定义3 设t∈[0,1],k,M为正整数,则式(7)为第二类Chebyshev小波基函数。 Ψnm(t)=Ψ(k,n,m,t)= (7) Um(t)是在区间[0,1]上的m阶第二类Chebyshev多项式。 若定义在区间[0,1]的函数f(t)是平方可积的,那么f(t)可以用第二类Chebyshev小波展开 (8) 其中: (9) 截取等式(8)有限项: (10) 这里 C=[c10,c11,…c1M-1,c20,c21,…,c2M-1,…,c2k-10,…,c2k-1M-1,]T Ψ(t)=[Ψ10,Ψ11,…Ψ1M-1,Ψ20,…,Ψ2M-1,…,Ψ2k-10,…,Ψ2k-1M-1] 下面给出本文的2个定理。 定理1 第二类Chebyshev小波变阶微分算子矩阵是 证明 首先定义矩阵-向量变换, ak=(ak1,ak2,…,akn),k=1,2,…,m即 T=(1,t,…,tMt-1)T,对Vxt进行微分得 (11) 其中:Dx,Dq分别是Vxt的微分算子矩阵和变分数阶微分算子矩阵。 由分数阶微分的性质得: (12) 由式(5)可以得到 (13) j=1,2,…,Mt-1;EMx是Mx阶的单位矩阵;0表示零矩阵。 定义二维小波向量VΨ=,其中Ψx=(ψnm(x))Nx×Mx,Ψt=(ψnm(t))Nt×Mt,Nx=2kx-1,Nt=2kt-1,那么第二类Chebyshev小波矩阵为IU,其中:U是MN行M列的矩阵(M=MxMt,N=NxN),U中的每行元素是二维小波向量Vψ中对应行的以为基的系数;I是MN阶对角方阵,其对角线上元素是小波向量Vψ中对应行的小波的选择函数。 (14) 证毕。 定理2 函数f:[0,1]→是m阶连续可导,且f∈Cm[0,1],若是f(t)的最佳逼近,则有误差边界 (15) 两边同时开平方 (16) 则定理得证。 从(15)式可以得出当k→∞时, (17) 选取合适数量的N个节点pij=(xi,tj)∈Ω,这里需要注意所选节点要避开选择函数的端点,将其代入上面的方程得到关于C=(cij)Mt×Mx的方程组, (18) 例如考虑如下方程 (19) f(x,t)=20x2(1-x)· 20(t+1)2(1-3x) 此方程的准确解为u(x,t)=10x2(1-x)(1+t)2。 用Mathematica9.0解得的数值解和精确解的绝对误差如图1和图2所示。 图1 kx=2,kt=1,Mx=4,Mt=4的绝对误差 图2 kx=1,kt=3,Mx=4,Mt=3的绝对误差 46.7415.58-15.58-7.795.181.73-1.73-0.860.140.05-0.05-0.0269.7523.25-23.25-11.626.332.11-2.11-1.050.140.05-0.05-0.0297.3632.45-32.45-16.237.482.49-2.49-1.250.140.05-0.05-0.02129.5743.19-43.19-21.608.632.88-2.88-1.440.140.05-0.05-0.02æèççççççççççççöø÷÷÷÷÷÷÷÷÷÷÷÷ 65.212.12-1.7604.51514.641.6205.0201.620.130-2.51-0.81-0.060155.5050.444.210-35.12-11.390.950-25.08-8.13-0.680-2.51-0.81-6.800æèççççççççöø÷÷÷÷÷÷÷÷ 由以上算例可以看出,用此方法求解得的数值解和精确解的误差达到了10-4,证明了该算法的有效性。 本文主要利用Chebyshev小波求解一类变时间分数阶的扩散方程的数值解。充分运用变分数阶微积分的性质推导出了Chebyshev小波的变阶算子矩阵,进一步给出了数值算法。从数值算例可以看到,用这种方法求此类变阶扩散方程的数值解时,随着所选取的离散点数的增多,其精确度就越高。 [1] SAMKO S G.Fractional integration and differentiation of variable order[J].Analysis Mathematica,2005,21(3):213-236. [2] LORENZO C F,HARTLEY T T.Variable order and distributed order fractional operators[J].Nonlinear Dynamics,2002,29(1-4): 57-98. [3] COIMBRA C F M.Mechanics with variable-order differential operators[J].Ann Phys,2003,12(11-12):692-703. [4] PEDRO H T C,KOBAYASHI M H,PEREIRA J M C,et al.Variable order modeling of diffusive-convective effects on the oscillatory flow past a sphere[J]. Journal of Vibration and Control,2008,14(9-10):1659-1672. [5] SUN H G, CHEN W, CHEN Y Q.Variable-order fractional differential operators in anomalous diffusion modeling[J].Physica A,2009,388(21):4586-4592. [6] LIN R,LIU F,ANH V,et al.Stability and convergence of a new explicit finite-difference approximation for the variable-order nonlinear fractional diffusion equation[J].Appl Math Comput,2009,212(2):435-445. [7] FIU F,YANG C,BURRAGE K.Numerical method and analytical technique of the modified anomalous subdiffusion equation with a nonlinear source term[J].Journal of Computational and Applied Mathematics,2009,231(1):160-176. [8] CHEN C M,LIU F,ANH V,et al.Numerical schemes with high spatial accuracy for a variable-order anomalous subdiffusion equation[J].SIAM J Sci Comput,2010,32(4):1740-1760. [9] CHEN C M,LIU F,ANH V,et al.Numerical methods and multivariate extrapolation of a two-dimensional anomalous subdiffusion equation[J].Numerical Algorithms,2010,54(1):1-21. [10] DIAZ G,COIMBRA C F M.Nonlinear dynamics and control of a variable order oscillator with application to the van der Pol equation[J].Nolinear Dyn,2009,56 (1-2):145-157. [11] 沈淑君.变时间分数阶扩散方程的数值模拟[J].莆田学院学报,2011,18(5):5-9. [12] 于强,刘发旺.时间分数阶反应-扩散方程的隐式差分近似[J],厦门大学学报(自然科学版),2006,45(3):315-319. [13] DOHA E H,BHRAWY A H,EZZ-ElDIEN S S.A chebyshev spectral method based on operational matrix for initial and boundary value problems of fractional order[J].Comput Math Appl,2011,62(5):2364-2373. [14] WANG Y X,FAN Q B.The second kind Chebyshev wavelet method for solving fractional differential equations[J].Appl Math Comput,2012,218(17):8592-8601. Numerical Solution of the Variable Order Time Fractional Diffusion Equation Using Chebyshev Wavelets XUYan1,ZHANGMin1,HANYongjie2*,HUANGZexia2 (1.Basic Department,University for Science&Technology Sichuan, Chengdu 611745, China;2.College of Science,Xihua University,Chengdu 610039,China) This paper presents an estimation method to calculate the variable order time fractional diffusion equation using the second kind Chebyshev wavelets function. The proposed operational matrixes of the second kind Chebyshev wavelet (SCW) is utilized to transform the fractional equation to a set of linear equations. Method of least square is used to solve the set of linear equations. The accuracy and performance of the method is demonstrated by numerical examples. variable order time fractional diffusion equation; second kind Chebyshev wavelet; operational matrix; numerical solution 10.13542/j.cnki.51-1747/tn.2016.04.017 2016-05-21 国家自然科学基金“概率和平均框架下一系列Sobolev空间中的函数逼近与恢复”(15233593);四川省教育厅基金“借助局部化采样方法研究频谱有限宽平稳过程”(15233448) 许燕(1987— ),女(汉族),河南商丘人,助教,硕士,研究方向:函数逼近论。 韩永杰(1986— ),男(汉族),四川成都人,讲师,博士,研究方向:函数逼近论,通信作者邮箱:xuyan345@163.com。 O241.8 A 2095-5383(2016)04-0001-04
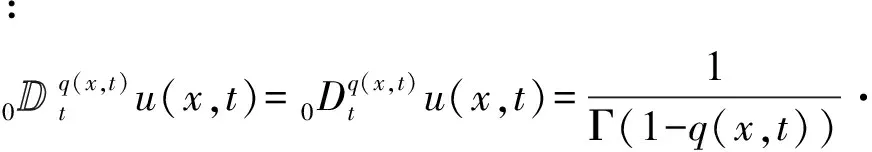
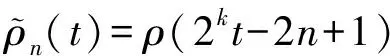
2 主要定理及数值算法
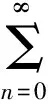

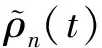



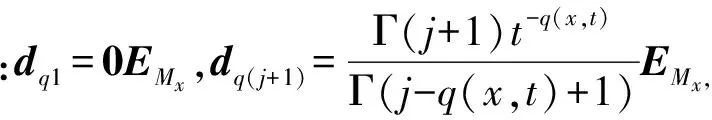
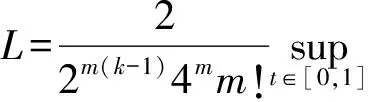
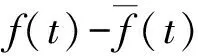
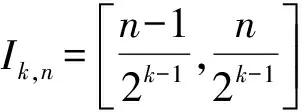
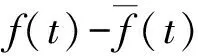
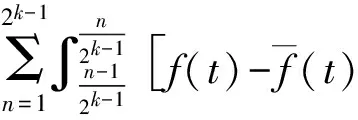
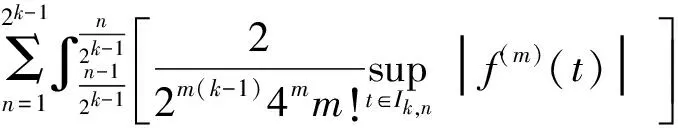
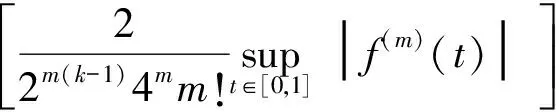
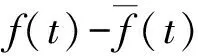
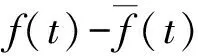
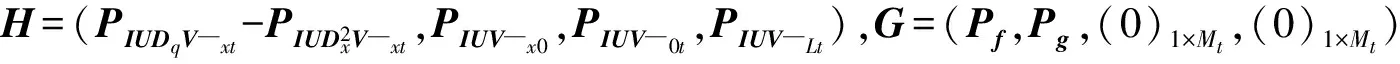
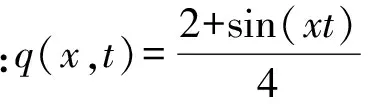


3 结语
