基于Taguchi方法的复合材料易碎盖结构参数设计①

蔡登安，吴秀平，杨国平，王校培，周光明

(1.南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016；2.中国人民解放军总参谋部第六十研究所，南京 210016)

基于Taguchi方法的复合材料易碎盖结构参数设计①

蔡登安1，吴秀平2，杨国平2，王校培1，周光明1

(1.南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016；2.中国人民解放军总参谋部第六十研究所，南京 210016)

为获得冲破性能稳定的复合材料易碎盖，对影响其性能的主要结构参数进行了分析研究。采用Taguchi试验设计方法，分析了结构参数薄弱区高度、内外侧搭接高度及厚度对易碎盖冲破性能的影响规律。结合信噪比、极差分析和指标趋势分析，比较了不同结构参数及因素水平对冲破性能的影响程度，获得了最优薄弱区结构参数组合。结果表明，薄弱区高度对易碎盖冲破性能影响最为显著，内外侧布条搭接高度及厚度对冲破性能影响较小；薄弱区高度为18 mm、内外侧布条搭接高度分别为4 mm和5 mm、搭接厚度分别为0.1 mm和0.2 mm时，易碎盖的冲破性能最接近设计目标；Taguchi方法分析结果与试验结果吻合，验证了该方法的准确性和有效性。

Taguchi试验方法；复合材料；易碎盖；结构参数；冲破性能

0 引言

纤维增强复合材料因其轻质高强的优越性能，而被广泛用于航空航天、机械、能源等领域[1-2]。军事及工业轻质化结构材料的应用，促进了纤维增强复合材料的不断发展。近年来，鉴于纤维增强复合材料的优越性能，导弹发射筒的密封箱盖也广泛采用此类材料[3-5]。使用纤维增强复合材料制作的易碎发射箱盖，在日常储压情况下，能保持导弹发射箱内的气压，导弹发射时，在一定压力条件下，易碎盖抛出部分整体抛开，使得导弹顺利发射出去。

为保证易碎盖顺利抛开，通常在复合材料易碎盖四周设置薄弱区结构[6]。针对薄弱区结构参数的变化对易碎盖整体性能的影响，较多的研究者开展了广泛的数值分析研究。Kam[7-8]等结合蔡-吴失效准则，分析了一定薄弱区结构的易碎盖分别承受内、外压载荷时的破坏形式。孙志彬[9]等通过设计薄弱区结构形式及搭接厚度，进行了易碎盖破坏过程的动力学仿真分析，确定了改变薄弱区结构强度来实现易碎盖按预定轨迹侧抛的设计方案。钱元[10-11]等针对易碎盖薄弱区结构，进行了静态及瞬态数值模拟，并根据模拟结果，对易碎盖结构参数进行了优化，获得了冲破性能较好的复合材料易碎盖。

为获得结构性能稳定的复合材料易碎盖，无论是对理论或数值分析结果的验证，还是对薄弱区结构性能的考察，都需要设计合理的试验方案，进行易碎盖冲破试验研究。而现有的研究成果中，对不同薄弱区结构参数的试验设计考虑较少，往往无法获得较精确而全面的易碎盖冲破性能试验结果。在易碎盖的结构设计过程中，传统方法很难准确地获得薄弱区结构参数，如薄弱区高度、搭接厚度及搭接高度对易碎盖冲破性能的影响规律，并在此基础上获得较好的薄弱区结构参数组合。

本文根据Taguchi方法[12-16]，设计合理的成型方案，对纤维增强复合材料易碎盖薄弱区结构参数进行了研究，分析了各结构参数对易碎盖整体冲破性能的影响规律，最后讨论了最优薄弱区结构参数组合。

1 试验方法

1.1 材料

纤维增强复合材料易碎盖主要采用E型平纹玻璃纤维机织布和E51型环氧树脂。该型双向纤维布的面密度为210 g/m2，树脂为WSR618系列环氧树脂，树脂固化剂采用苯二甲胺，添加剂为邻苯二甲酸二丁酯。易碎盖主体结构采用的铺层顺序为[(0/90°)(±45°)]2s，主体结构形状及尺寸如图1所示。

图1 易碎盖结构形状及尺寸Fig.1 Structure and dimension of the frangible cover

1.2 试验设计

本文研究的复合材料易碎盖的设计冲破压强(pf)范围为0.6～0.7 MPa。以易碎盖冲破性能为指标，利用Taguchi方法，对复合材料易碎盖薄弱区的结构参数进行优化，研究薄弱区各结构参数对易碎盖冲破性能的影响规律。易碎盖薄弱区结构如图2所示，其中胶接区域形状为等腰直角三角形，直角边边长为复合材料易碎盖壁厚的1/2。影响易碎盖冲破性能的薄弱区结构参数主要涉及5个因素：A—薄弱区高度；B—内侧布条搭接高度；C—外侧布条搭接高度；D—内侧布条搭接厚度；E—外侧布条搭接厚度；各因素水平见表1。试验采用Ln(mk)正交表(其中，试验组数n=16，因素水平数m=4，因素个数k=5，见表2)制备16种不同薄弱区结构参数的易碎盖，测试其冲破性能。

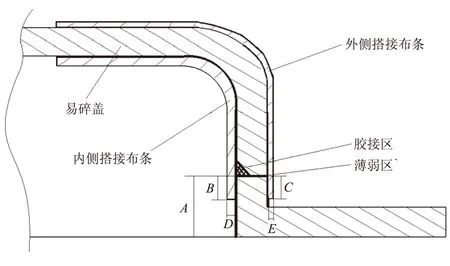
图2 易碎盖薄弱区结构Fig.2 Weak zone structure of the frangible cover表1 控制因素与水平Table 1 Control factors and their levels

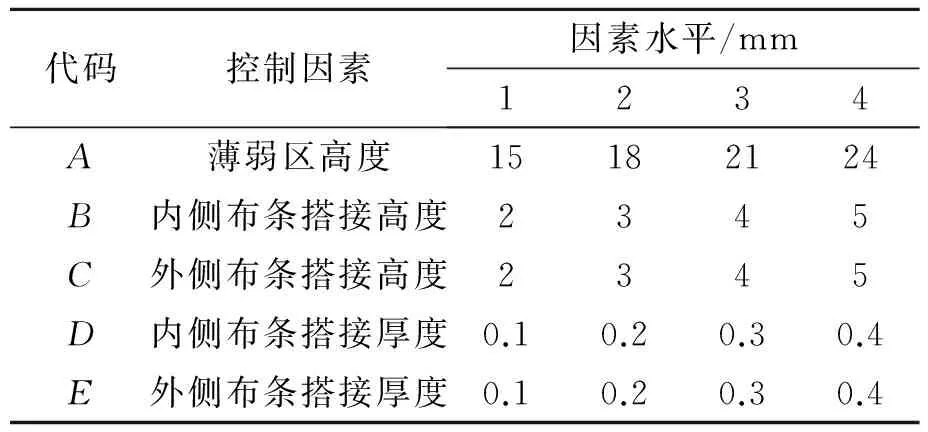
代码控制因素因素水平/mm1234A薄弱区高度15182124B内侧布条搭接高度2345C外侧布条搭接高度2345D内侧布条搭接厚度0.10.20.30.4E外侧布条搭接厚度0.10.20.30.4

1.3 试验

充压试验装置如图3所示，设置模拟发射筒型工装，连接气泵和压力表，采用密封垫圈密封，保证良好的气密性。

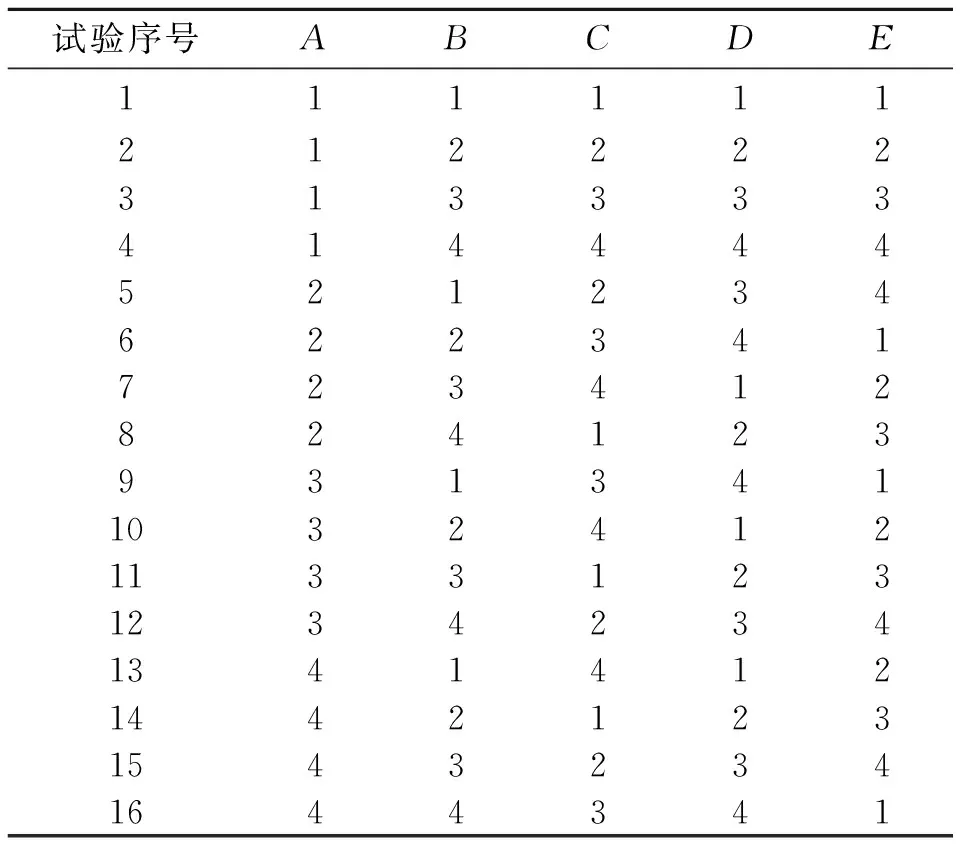
表2 L16(45)正交表Table 2 L16(45)orthogonal array

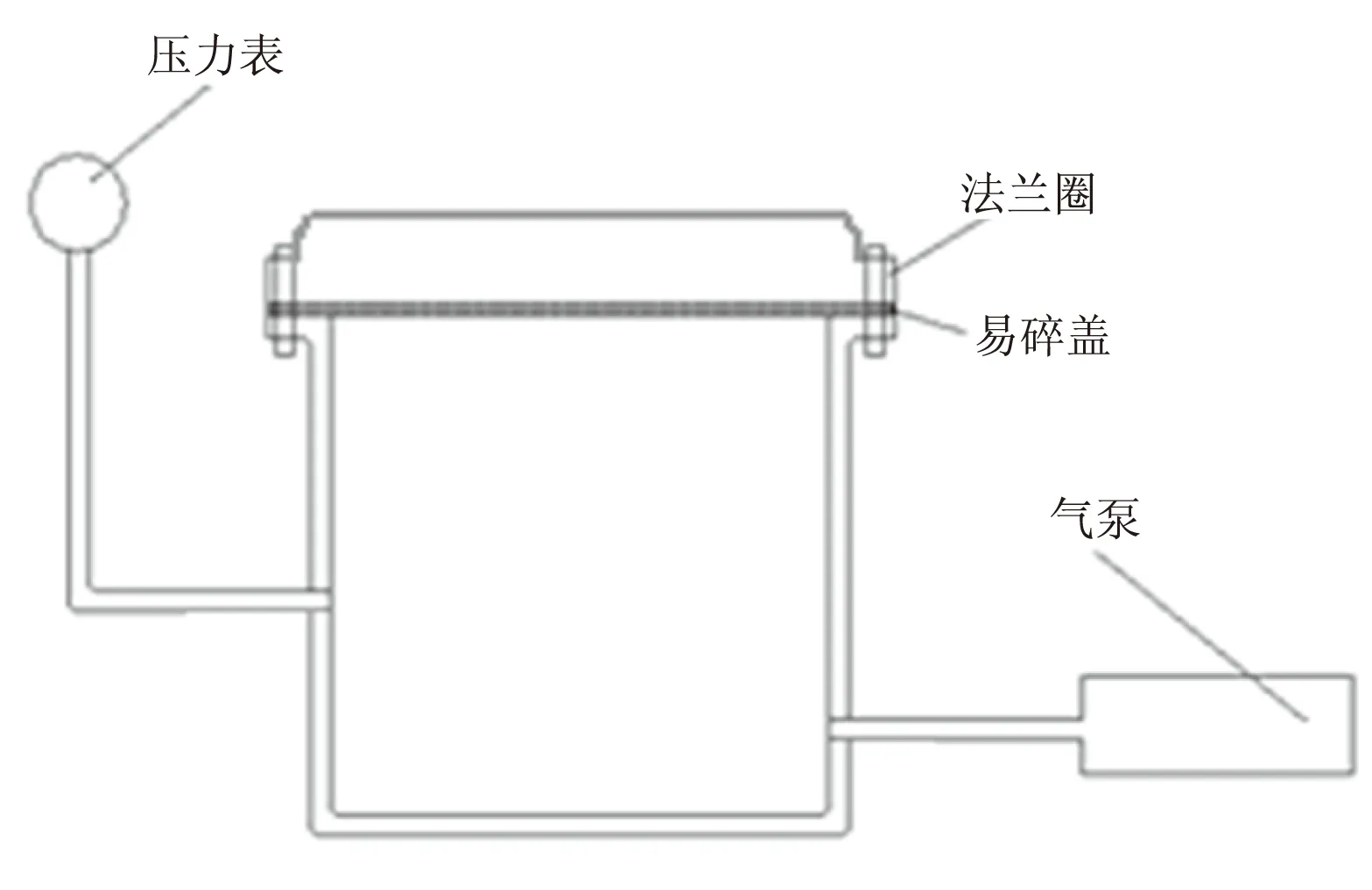
图3 充压试验装置Fig.3 Filling pressure test device

充压试验开始前，预先在试验装置内充气至压力为0.1 MPa，保持30 s，观察气密性。装置无漏气现象，卸载。再次进行充压试验，直至易碎盖被冲破，此过程加载速率为0.02 MPa/s。为保证周边设施及人身安全，需在试验装置周围设置保护框架及弹性绳索，防止易碎盖冲破后抛出部分造成损坏，如图4所示。

2 结果与分析

2.1 试验结果与信噪比

Taguchi方法中，提出了信噪比的概念，它是衡量产品质量稳定性波动大小的指标[17]。

本文采用式(1)信噪比公式[18]进行计算分析：

(1)

表3给出了16组易碎盖的冲破压强及其信噪比的计算结果，每组试验测试3个有效易碎盖。

图4 冲破试验保护装置Fig.4 Protective device of destructive test表3 冲破压强与信噪比Table 3 Failure pressure and signal-to-noise ratio

试验序号冲破压强pf/MPa1#2#3#平均值x-信噪比η/dB10.410.480.460.4513.8920.430.480.500.4714.7830.480.520.530.5116.9840.580.470.540.5317.8350.650.610.590.6227.6160.590.600.620.6026.3270.630.690.660.6631.5580.640.630.590.6228.6490.650.540.580.5922.47100.640.630.560.6125.43110.560.590.650.6024.09120.620.550.570.5822.39130.490.530.510.5117.02140.530.480.490.5016.39150.490.570.560.5418.74160.520.590.600.5721.15

2.2 极差分析

(2)

极差R反映了各列因素的水平变动时，试验指标的变动幅度。R越大，说明该因素对试验指标的影响越大，因此也就越重要。依据R的大小，即可判断因素的主次。表4中，RA>RB>RC>RD>RE，因此因素对试验指标影响的主次顺序为ABCDE。

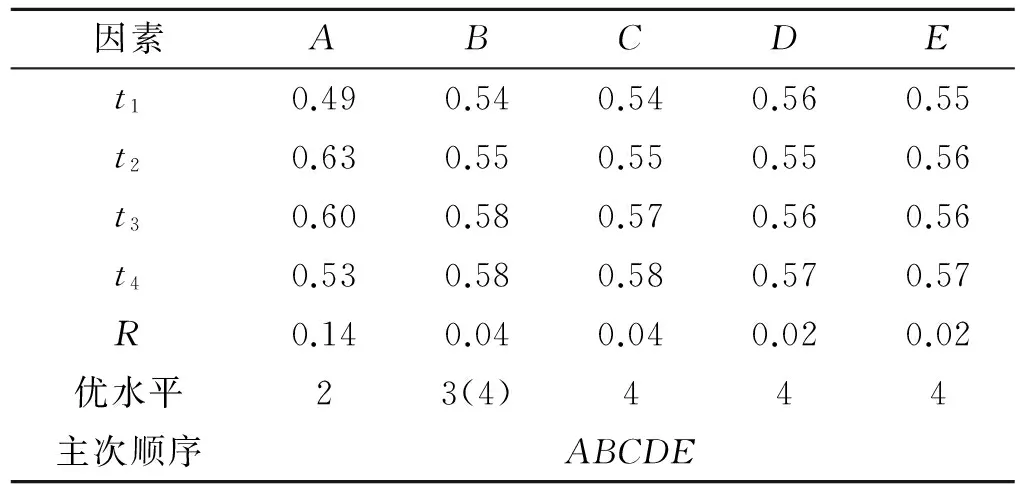
表4 易碎盖冲破压强极差分析Table 4 Range analysis on failure pressureof the frangible cover MPa

结合优水平与主次顺序，可得到各因素的最优组合为A2B3C4D4E4或A2B4C4D4E4。同样采用极差分析法，对表3中信噪比结果进行分析，分析结果见表5。

信噪比极差是指表5中任一列因素各水平的信噪比最大值与最小值之差，即

(3)

通过信噪比极差分析，结合优水平与主次顺序，可得到各因素的最优组合为A2B3C4E2D1。

表5 信噪比极差分析Table 5 Range analysis on signal-to-noise ratio dB

通过极差分析，获得了3种最优组合方案：A2B3C4D4E4、A2B4C4D4E4和A2B3C4E2D1。究竟哪个方案最佳，则需要进一步分析验证。

2.3 指标趋势

为了更直观地反映出各因素对试验指标的影响规律和趋势，绘制因素与指标趋势的关系图(因素水平为横坐标，试验指标为纵坐标)，如图5所示。

(a)因素A

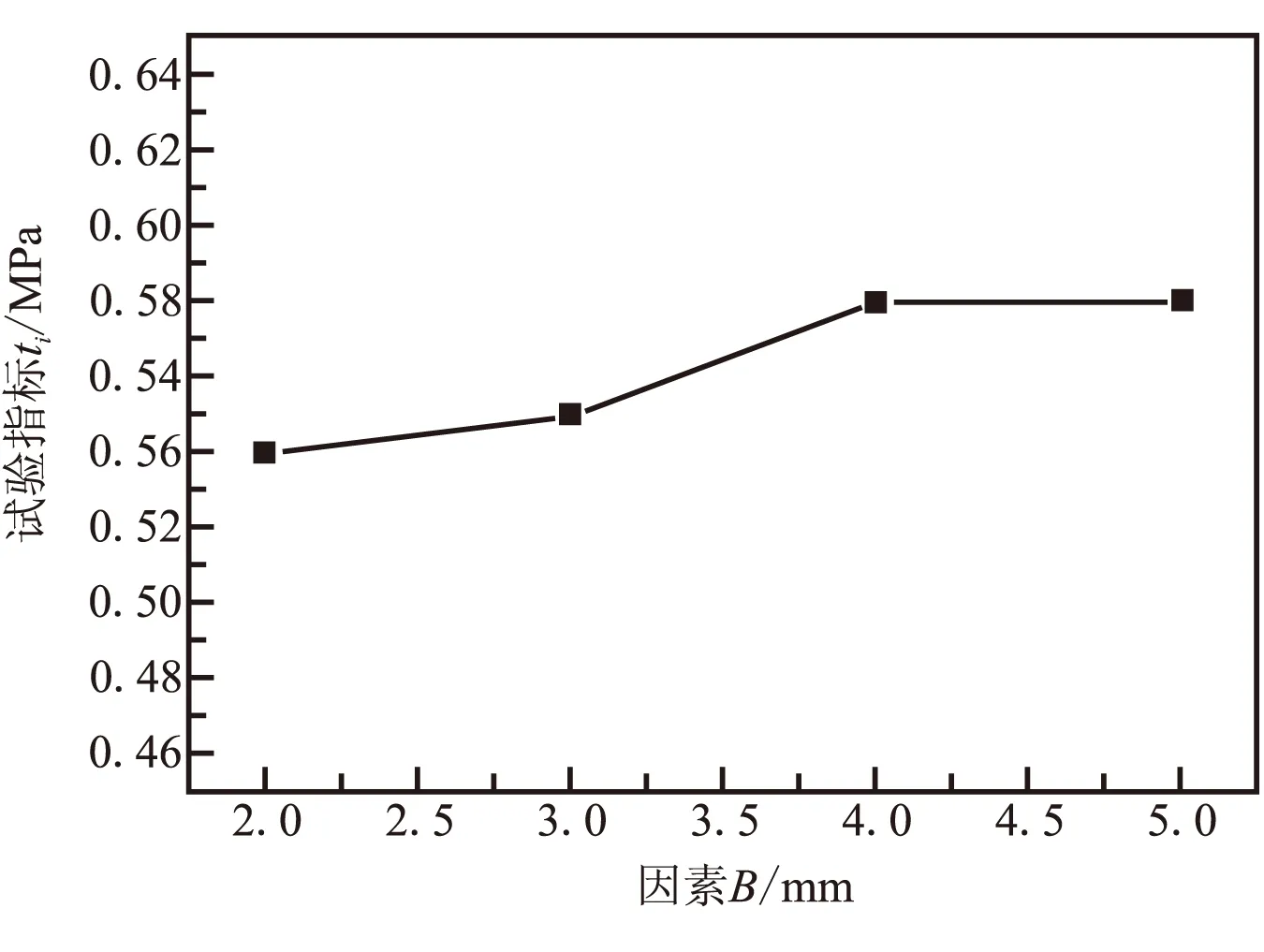
(b)因素B

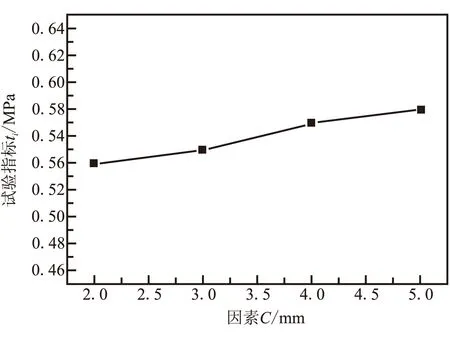
(c)因素C

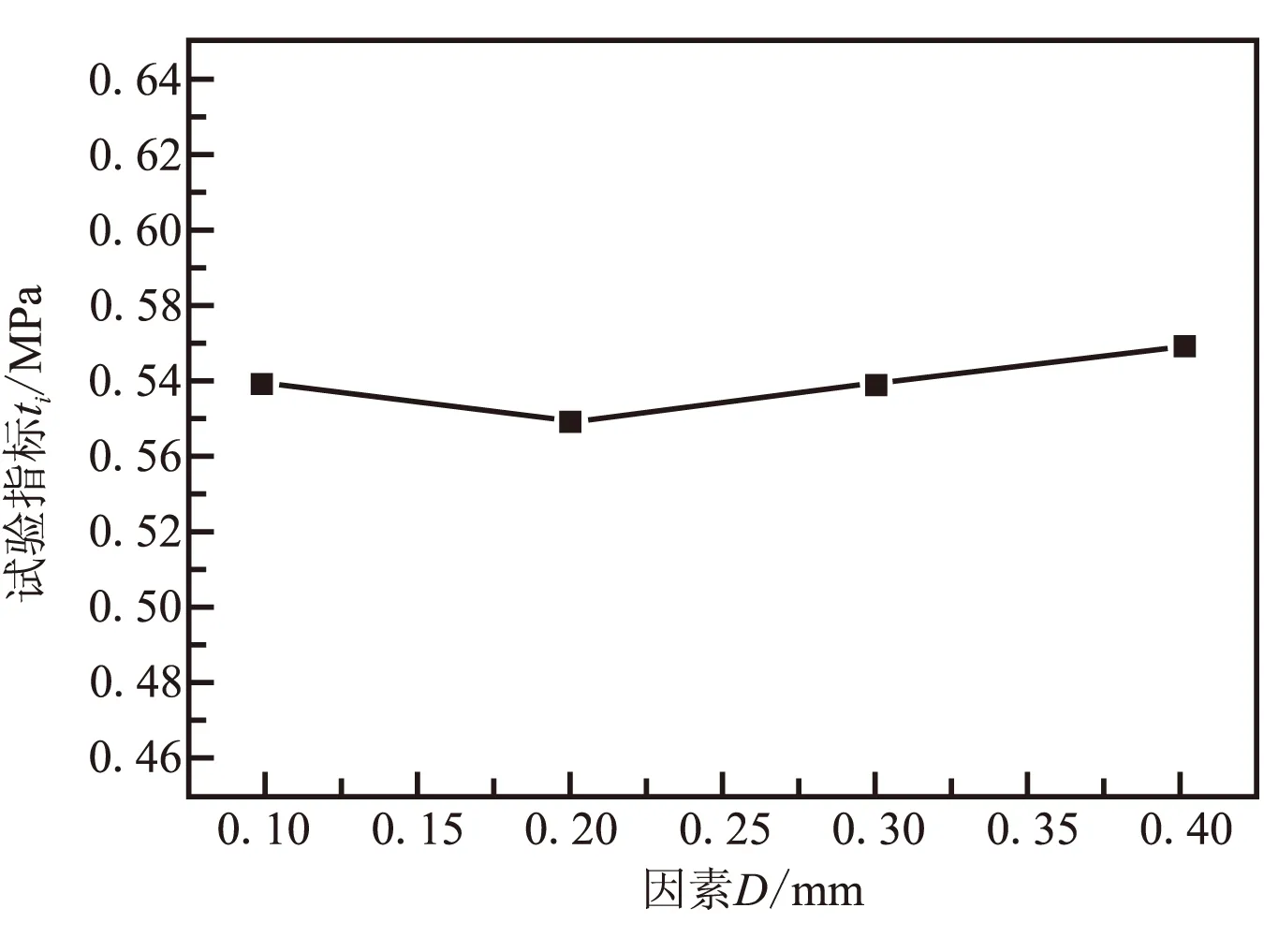
(d)因素D

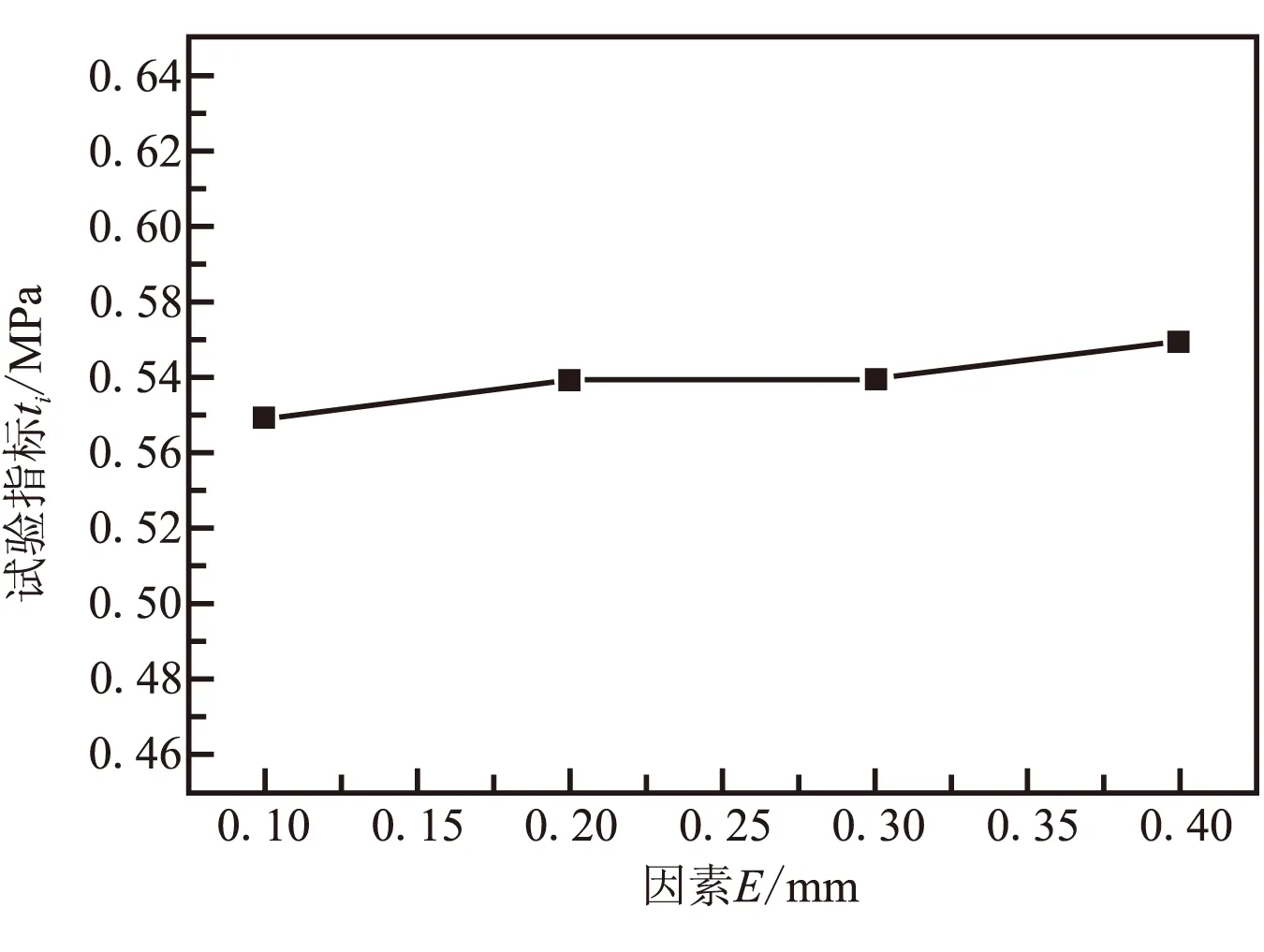
(e)因素E图5 影响因素与冲破压强趋势图Fig.5 Trend chart of factors and failure pressure

因素与试验指标趋势图直观地表现出试验指标随因素水平的变化而变化的趋势。由图5可见，因素A(薄弱区高度)对试验指标(冲破压力)的影响最大，试验指标随因素水平的变化起伏较大；而因素B(内侧布条搭接高度)、因素C(外侧布条搭接高度)、因素D(内侧布条搭接厚度)和因素E(外侧布条搭接厚度)水平的改变对试验指标的影响较小，虽然试验指标随着因素水平的增加有小幅增加，但试验指标随因素水平的变化起伏较小。因而说明，因素A是控制易碎盖冲破性能的最主要的影响因素。上述3种最优组合方案也验证了这样的推断。

2.4 结构参数分析

针对上述几种最优组合方案，可采用试验目标信噪比预测结果比较各种方案的稳定性，从而选取最佳参数组合。针对本文的试验指标及试验结果而言，信噪比越大，说明试验方案越稳定、波动性越小。采用的预测公式[19]如下：

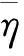
方案A2B3C4D4E4的信噪比预测结果为31.59dB，方案A2B4C4D4E4的信噪比预测结果为31.26dB。这2个组合方案并未出现在设计的正交表中，因而无对应的试验值与之比较。对于方案A2B3C4E2D1，其信噪比预测结果为29.95dB。在正交表中对应第7组试验，信噪比的试验结果为31.55dB，预测值与试验值偏差5.07%。由此可见，预测的信噪比具有一定的可信度和再现性。结合3种方案信噪比预测值的大小比较结果，以及正交表中易碎盖冲破压力与试验目标值的比较结果，3种方案的优先顺序依次为A2B3C4D4E4、A2B3C4E2D1、A2B4C4D4E4。方案A2B3C4D4E4是最佳的参数组合。值得注意的是方案A2B3C4D4E4中，因素D和E的水平均较高，而根据图5可知，因素D和E的水平变化对试验指标的影响非常小。根据以下易碎盖结构参数的分析研究结果，最终采用方案A2B3C4E2D1为合理的易碎盖最优参数组合。下面对易碎盖各结构参数的影响规律进行讨论分析。

对于因素A(薄弱区高度)。易碎盖在一定气压下的分离面位于薄弱区位置，即薄弱区是易碎盖结构强度最低的位置。因此，薄弱区的位置对易碎盖的冲破压强起着至关重要的作用。在内部均匀气压作用下，易碎盖环向侧壁由底部至顶部的应力分布并不一致。当内部气压不断增加时，易碎盖侧壁局部位置的应力水平达到薄弱区结构的承载极限(假设相同结构参数的薄弱区其承载极限是一定的)，而此时薄弱区也恰好位于此位置，则易碎盖被冲破分离。

对于因素B(内侧布条搭接高度)。内侧搭接纤维布条连接易碎盖内侧抛出部分和法兰框架部分，并对两部分连接处的胶接部分进行密封和加强，避免胶接区域直接暴露于气压载荷下，防止胶接面因过早产生裂纹而分离。因此，易碎盖内侧布条搭接高度对薄弱区承载能力具有一定的增强作用，但随着内侧布条搭接高度的增加，试验指标增幅有限，最终趋于平缓(见图5)。此外，在试验过程中，如果内侧布条搭接高度过大，亦会出现易碎盖无法冲破的现象(其原因主要是内部加载气压达到一定值时，胶接区域破坏，但搭接布条仍未与易碎盖框架分离，内部气体大量外泄，无法继续加载，最终导致易碎盖无法冲破)。因此，搭接布条高度的选择并非越大越好，需保证易碎盖能够顺利冲破。

对于因素C(外侧布条搭接高度)。与内侧布条类似，搭接高度对薄弱区结构的承载能力具有一定的影响。但由于易碎盖主要受内部气压作用，因而外侧布条起到一定的密封作用外，对易碎盖冲破压强的影响作用较小。通过影响因素与冲破压强趋势图亦可看出，外侧搭接布条高度的增加，对易碎盖冲破压力的提高也非常有限。

对于因素D和因素E(内、外侧布条搭接厚度)。一般而言，搭接厚度的增加会提高搭接接头的强度，但研究表明，相同条件下，随着搭接厚度的不断增加，搭接接头强度增加有限，最终趋于定值。图5中的指标趋势图也表明，易碎盖内外侧布条搭接厚度对易碎盖冲破压力的影响最小，试验指标随着该因素的变化基本维持稳定，冲破压强的最大差别仅为0.02MPa。同时，考虑工艺的简便与稳定以及工艺时间与成本，实际制作易碎盖时，并不会选取较大的内外侧布条搭接厚度。因此，最终采用方案A2B3C4E2D1为合理的易碎盖最优参数组合。

3 结论

(1)易碎盖主要结构参数中，薄弱区高度对易碎盖冲破性能具有显著影响；而内外侧布条搭接高度及厚度对冲破性能的影响较小。通过性噪比和极差分析，获得了A2B3C4D4E4、A2B3C4E2D1、A2B4C4D4E43种较优的组合方案。结合指标趋势图，考虑工艺的简便与稳定性，确定方案A2B3C4E2D1(即薄弱区高度18mm，内、外侧布条搭接高度分别为4mm和5mm，内、外侧布条搭接厚度分别为0.1mm和0.2mm)为易碎盖的最优结构参数组合。

(2)薄弱区是易碎盖强度最低的部位，因而对易碎盖的承载性能起着决定性作用。对于不同冲破性能要求的易碎盖，可结合Taguchi试验方法，优先考虑薄弱区位置(即薄弱区高度)的选取；然后，再确定其他结构参数的水平。

(3)通过Taguchi试验策略设计试验方案，采用极差分析法结合指标趋势分析，可判断出较优的结构参数组合方案。对于优先等级接近或在正交表中未出现的试验组合，可采用信噪比预测结果，进行进一步比较分析，同时结合工程实际，可最终确定最优的结构参数组合。

[1]SathishkumarTP,SatheeshkumarS,NaveenJ.Glassfiber-reinforcedpolymercomposites-areview[J].JournalofReinforcedPlasticsandComposites,2014,33(13):1258-1275.

[2] 邢丽英,蒋诗才,周正刚.先进树脂基复合材料制造技术进展[J].复合材料学报,2013,30(2):1-9.

[3] 傅德彬,姜毅.某导弹易碎盖的开启过程[J].固体火箭技术,2007,30(4):275-277.

[4] 周光明,袁卓伟,王新峰.整体冲破式复合材料薄膜盖的设计与试验研究[J].宇航学报,2007,28(3):707-712.

[5] Zeng W,Jiang Y.Failure analysis of a composite frangible cover based on transient dynamics[J].Applied Mechanics and Materials,2013,395:55-59.

[6] 曹然,周光明,钱元,等.复合材料易碎盖薄弱区结构的参数化设计[J].固体火箭技术,2015,38(4):549-553.

[7] Wu J H,Wang W T,Kam T Y.Failure analysis of a frangible laminated composite canister cover[J].Proceedings of the Institution of Mechanical Engineers,Part G:Journal of Aerospace Engineering,1999,213(3):187-195.

[8] Kam T Y,Wu J H,Wang W T.External failure pressure of a frangible laminated composite canister cover [J].Composite Structures,1999,47(1):563-569.

[9] 孙志彬,王新峰,周光明.圆形复合材料易碎盖定向分离[J].南京航空航天大学学报,2012,44(6):803-808.

[10] 钱元,周光明,贺卫东,等.复合材料易碎盖薄弱区结构设计分析[J].航空学报,2012,33(3):487-493.

[11] 钱元,周光明,贺卫东,等.轻质复合材料发射箱盖结构设计与参数优化[J].航空学报,2013,34(4):826-832.

[12] 洪斌,咸贵军,李惠.基于Taguchi方法的碳纤维复合材料拉挤工艺优化[J].工业建筑,2013,43(6):9-13.

[13] 段玉岗,刘芬芬,陈耀,等.纤维铺放压紧力及预浸带加热温度对复合材料力学性能的影响[J].复合材料学报,2012,29(4):148-156.

[14] Koksal S,Ficici F,Kayikci R,et al.Experimental optimization of dry sliding wear behavior of in situ AlB2/Al composite based on Taguchi's method[J].Materials & Design,2012,42:124-130.

[15] Gu F,Hall P,Miles N J,et al.Improvement of mechanical properties of recycled plastic blends via optimizing processing parameters using the Taguchi method and principal component analysis[J].Materials & Design,2014,62:189-198.

[16] 王岩,隋思涟.试验设计与MATLAB数据分析[M].清华大学出版社,2012.

[17] Jeyapaul R,Shahabudeen P,Krishnaiah K.Quality management research by considering multi-response problems in the Taguchi method—a review[J].The International Journal of Advanced Manufacturing Technology,2005,26(11-12):1331-1337.

[18] Zang C,Friswell M I,Mottershead J E.A review of robust optimal design and its application in dynamics[J].Computers & Structures,2005,83(4):315-326.

[19] Sahin Y.Optimization of testing parameters on the wear behaviour of metal matrix composites based on the Taguchi method[J].Materials Science and Engineering:A,2005,408(1):1-8.

(编辑：薛永利)

Design for structure parameters of composite frangible cover based on Taguchi’s method

CAI Deng-an1，WU Xiu-ping2，YANG Guo-ping2，WANG Xiao-pei1，ZHOU Guang-ming1

(1.State Key Laboratory of Mechanics and Control of Mechanical Structures，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China；2.The 60th Research Institute of the Headquarters of General Staff of Chinese People’s Liberation Army，Nanjing 210016，China)

In order to obtain a composite frangible cover with stable failure performance,the main structural parameters were analyzed and researched.The influence of structural parameters such as height of weak zone,height and thickness of inside and outside lapped layers on failure performance of the composite cover was studied by using Taguchi experiment design method.By analysis of signal-to-noise ratio,range analysis and index trend,the effect degree of different structure parameters and factor levels on failure performance were compared and the optimal parameter combination of weak zone structure was obtained.The results show that height of weak zone has significant influences on failure properties of the frangible cover and that the heights and thicknesses of the lapped layers have small effects on them.The failure pressure is most close to the design target when the height of weak zone is 18 mm,and the heights of inside and outside lapped layers are 4 mm and 5 mm,and the thicknesses are 0.1 mm and 0.2 mm respectively.The accuracy and effectiveness of Taguchi method were verified by the experimental results.

Taguchi experimental strategy；composite materials；frangible cover；structure parameter；failure performance

2015-11-29；

2016-01-06。

江苏省科技项目产学研联合创新基金(BY2014003-10)；南京市科技计划项目(201306010)；江苏省高校优势学科建设工程项目；江苏省研究生培养创新工程(KYLX_0222)；中央高校基本科研业务费专项资金；机械结构力学及控制国家重点实验室(南京航空航天大学)自主研究课题(0214G02)。

蔡登安(1988—)，男，博士生，主要从事复合材料结构设计及强度理论研究。E-mail：cda@nuaa.edu.cn

周光明(1966—)，男，教授，主要从事先进复合材料结构设计、复合成型及性能验证。E-mail：zhougm@nuaa.edu.cn

V214.8

A

1006-2793(2016)06-0797-06

10.7673/j.issn.1006-2793.2016.06.011