分数Brown运动驱动的非Lipschitz随机微分方程
2017-01-04冉启康
冉启康
(上海财经大学数学学院,上海 200433)
分数Brown运动驱动的非Lipschitz随机微分方程
冉启康
(上海财经大学数学学院,上海 200433)
讨论了一类带分数Brown运动的非Lipschitz增长的随机微分方程适应解的存在唯一性.关于分数Brown运动的随机积分有多种定义,本文使用一种广义Stieltjes积分定义方法,利用这种积分的性质,建立了一类由标准Brown运动和一个Hurst指数的分数Brown运动共同驱动的、系数为非Lipschitz增长的随机微分方程适应解的存在唯一性定理.
分数Brown运动;广义Stieltjes积分;非Lipschitz增长的SDE;适应解
1 预备及主要结论
设(Ω,F,P)是一个完备的概率空间,是其上的Hurst指数为H的分数Brown运动,本文只讨论的情形.自1940年Kolmogorov首次提出分数Brown运动以来,由于它在物理、金融、电信等众多领域有着广泛的应用而受到越来越多的关注.1968年,文献[1]首次给出了分数 Brown运动的基于标准 Brown运动的随机积分表达式.文献[2.3]中对这个积分表达式进行了改进.近年来,人们给出了关于分数布朗运动的多种随机积分的定义,因为当时,分数布朗运动不是半鞅,经典的Itˆo积分不再适应,人们发现,当时,随机积分可定义为Riemann和的极限,但此积分不满足性质文献[4]中建立了当时一个基于Wick乘积的随机积分理论,文献[5]将此积分推广到0<H<1的情形.在文献[6]中建立了一种广义Stieltjes积分,这种积分对标准Brown运动和分数Brown运动适用.在文献[7]中利用这种积分方法证明了SDE,0≤t≤T,当b,σW满足Lipschitz增长条件时,适应解的存在唯一性结果.本文讨论方程
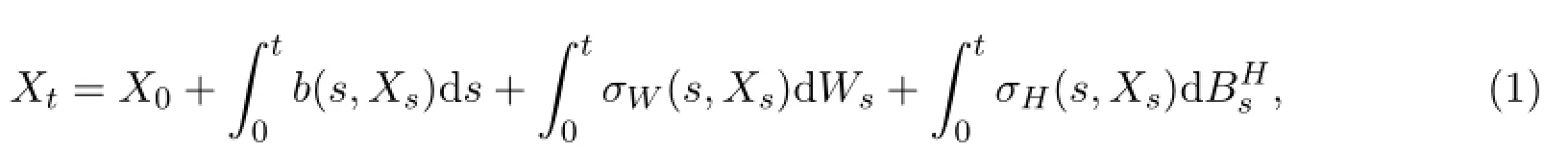
我们证明了当b满足非Lipschitz增长条件时,方程(2)存在唯一性的适应解.
下面,介绍广义Stieltjes积分的定义及SDE(2)解空间的定义.
设(Ω,F,P)是一个完备的概率空间,是其上的d-维标准Brown运动,是其上的Hurst指数为的d-维分数Brown运动,且X0,W,BH相互独立.记
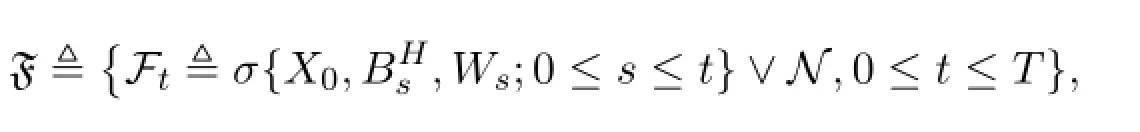
其中N表示F的所有P零集.为了定义SDE的解空间,还需要一个比更大的σ-代数流使得:是右连续的,包含的所有P零集,且X0,BH是可测的,W是一个运动.又表示
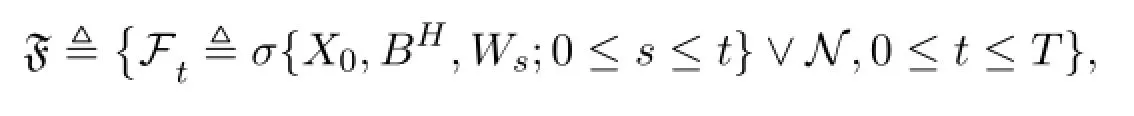
为了定义广义Stieljes积分和SDE的解空间,需要下列函数空间:

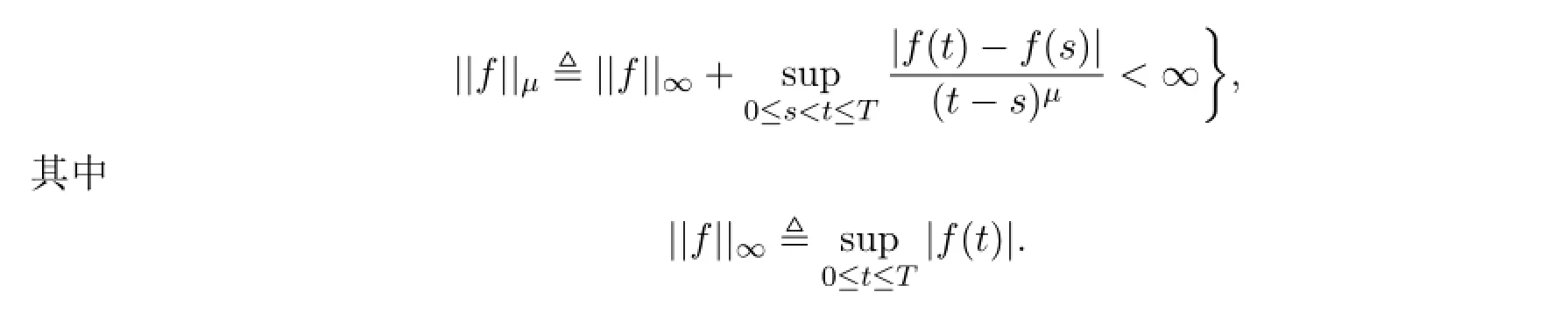
根据上述记号,下列性质是直接的:
引理1.1(1)对任意0<ϵ<α,有
(2)对任意ϵ>0,有
定义 1.1设称
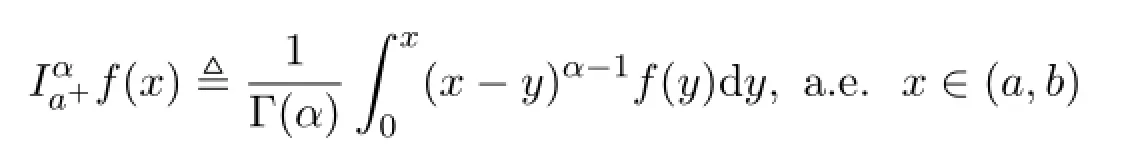
为f的α阶分数Riemann-Liouville左积分;称
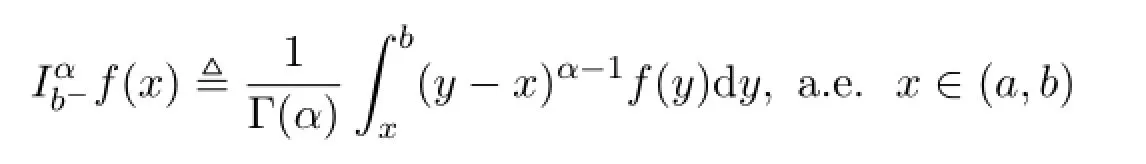
为f的α阶分数Riemann-Liouville右积分.
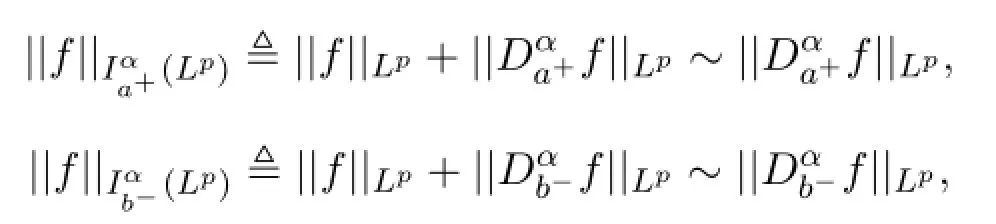
定义1.2如果其中0<α<1,p≥1,定义f的Weyl导数为
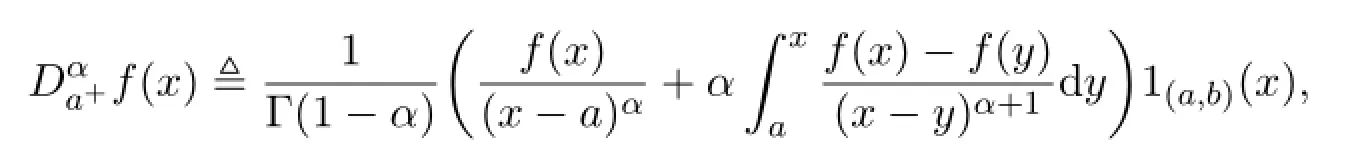
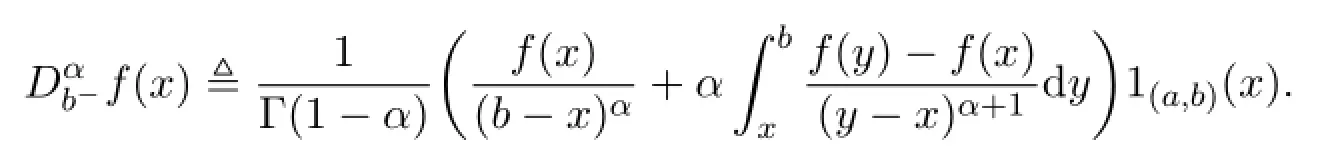
引理 1.2[12](1)如果那么,
记
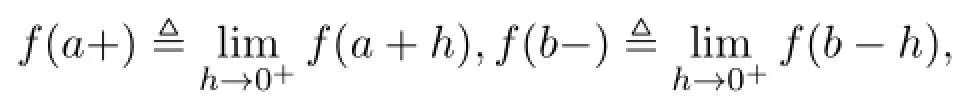
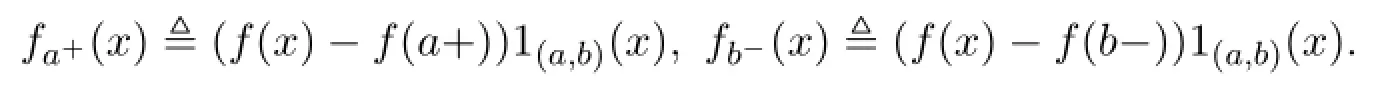
定义 1.3[6](广义Stieltjes积分)设f,g是两个定义在(a,b)上的函数,满足:
(1)f(a+),g(a+),g(b-)存在;
(2)存在p,q≥1,0<α<1,使得
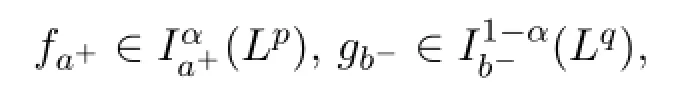
那么,f关于g的广义Stieltjes积分定义为
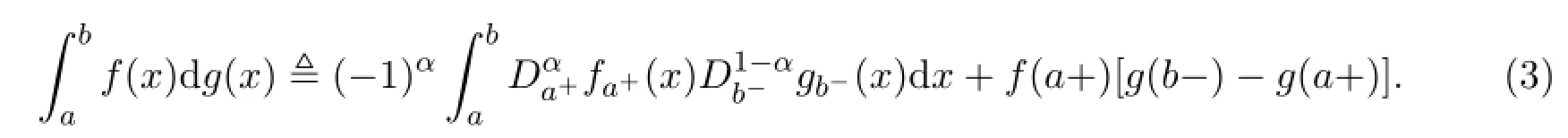
特别地,如果αp<1,因为所以
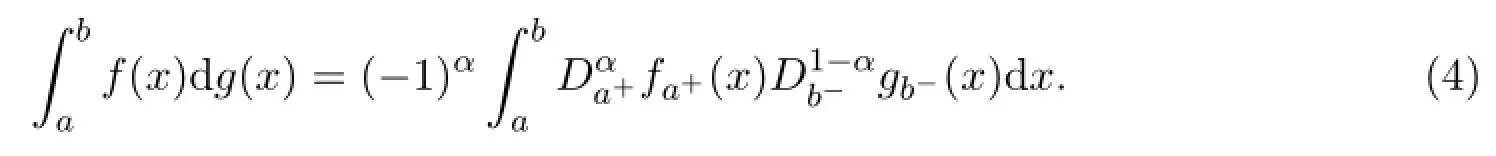
由文献[6]知:如果f∈Cλ(a,b),g∈Cµ(a,b),且λ+µ>1,则存在 1-µ<α<λ,使得存在,满足(4)式,且它与普通Stieltjes积分是一致的.
由广义Stieltjes积分的定义直接得到下列结论成立:
引理1.3(1)如果那么,对任意t∈[0,T],存在,且

其中
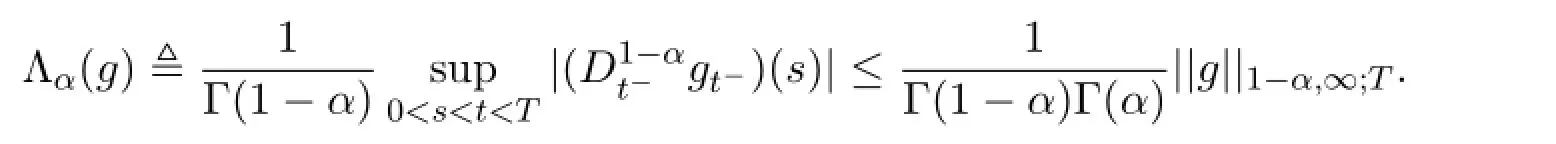
本文中,对b,σW,σH的假设如下:

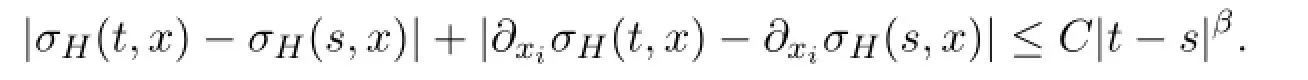
定义1.4用表示满足下列条件的d-维随机过程X={Xt,0≤t≤T}的全体:
(1)X是适应过程;
(2)X的几乎所有路径属于且满足
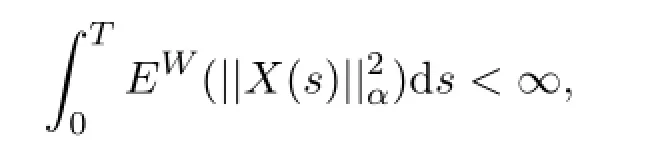
其中,EW(X)表示条件期望
主要结论如下:
定理1.1如果条件(H1),(H2)及(H3)成立,{σW(t),0≤t≤T}是循序可测的,且存在常数B>0,(H4)
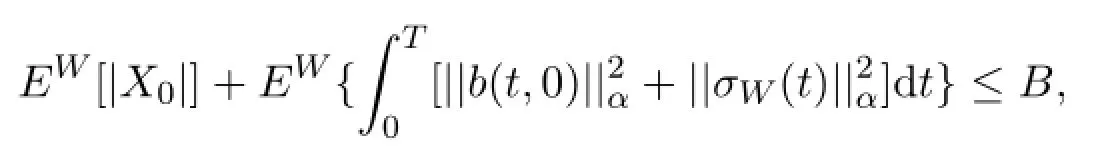
那么,当T适当小时,方程(2)存在唯一解
2 主要结论的证明
在证明主要结论前,需要引入几个引理:
引理2.1如果条件(H1),(H3)成立,那么对任意,t∈[0,T],有
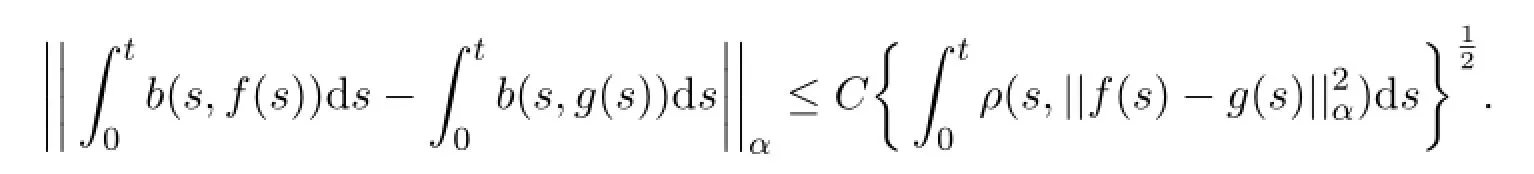

引理2.2[7]如果那么
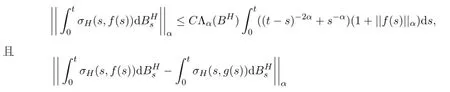

引理2.3[7]设u={u(t),t∈[0,T]}是一个d×d-维适应过程,且满足
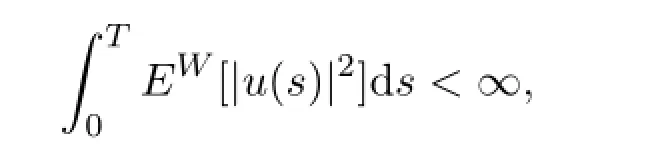
那么,对任意t∈[0,T],a.s.意义下有
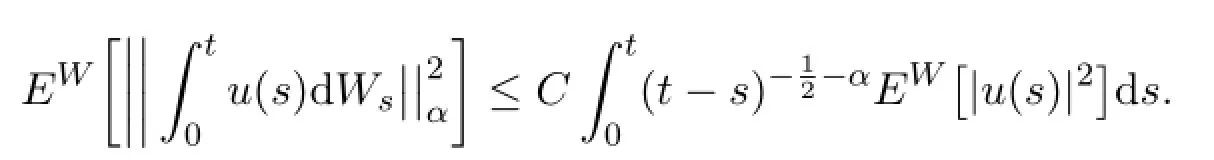


为了证明存在性,还需要下列两个引理:
引理2.4如果条件(H1)-(H4)成立,则存在常数b>0,使得对任意n≥1,有
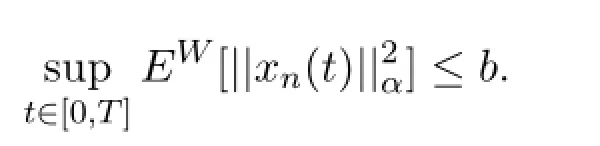
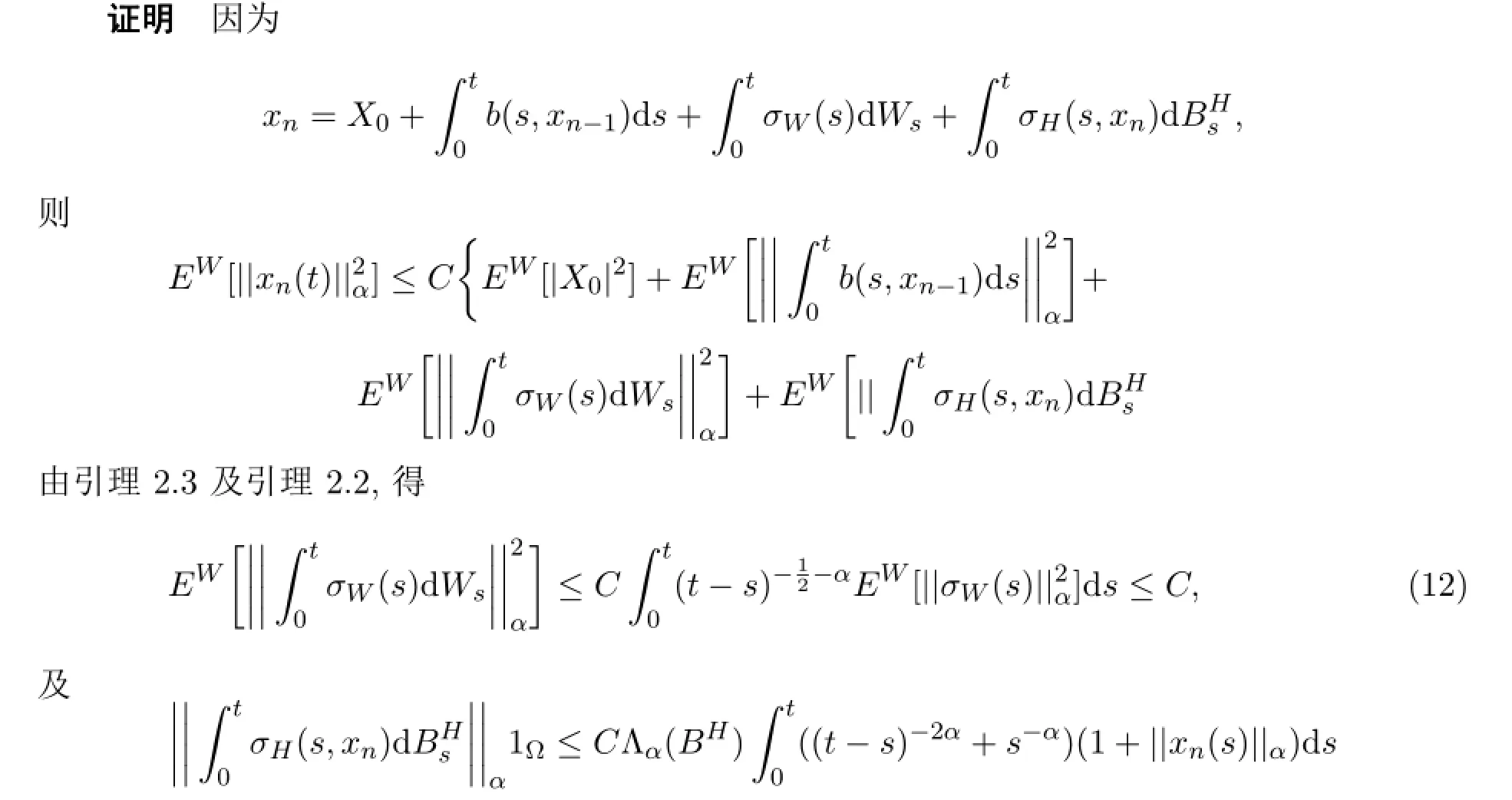

引理2.5如果条件(H1),(H2),(H3)成立,则对任意t∈[0,T],n,m≥1,有
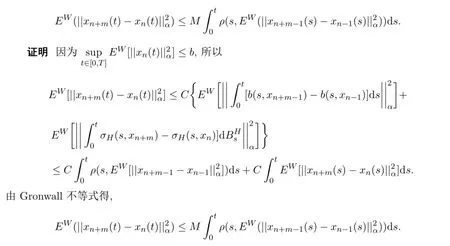


[1]Mandelbrot B B,Van Ness J W.Fractional Brownian motion,fractional noises and application[J].SIAM Review,1968,10:422-437.
[2]Decreudefond L.Üstünel A S.Stochastic analysis of the fractional Brownian motion[J].Potential Anal., 1999,10:177-214.
[3]Hu Y Z.Integral transformations and anticipative calculus for fractional Brownian motions[J].Mem.Amer.Math.Soc.,2005,no.825.
[4]Duncan T E,Hu Y Z,Pasik-Duncanb B.Stochastic calculus for fractional Brownian motion,I:Theory[J].SlAM Journal of Control and optimization,2000,38(2):582-612.
[5]Elliott R J,Van Der Hoek J.A general fractional white theory and applications to finance[J].Mathematical Finance,2003,13(2):301-330.
[6]Zähle M.Integration with respect to fractal functions and stochastic calculus I[J].Prob.Theory Relat.Fields,1998,111:333-344.
[7]Guerra J,Nualart D.Stochastic differential equations driven by fractional brownian motion and standard brownian motion[J].Stochastic Analysis and Applications,2008,26:1053-1075.
[8]王赢,王向荣.一类非Lipschitz条件的Backward SDE适应解的存在唯一性[J].应用概率统计,2003,19(3):245-251.
[9]毛伟.带有非Lipschitz系数的跳扩散微分方程解的存在性[J].华东师范大学学报,2016,50(1):10-14.
[10]Nualart D,Răscanu A.Differential equations driven by fractional Brownian motion[J].Collect.Math., 2002,53:55-81.
[11]Bihari I.A generalization of a lamma of Bellman and its application to uniqueness problem of fifferential equations[J].Acta Math.Acad Sci Hunger,1956,7:71-94.
[12]Samko S G,Kilbas A A,Marichev O I.Fractional Integrals and Derivatives,Theory and Applications[J].Gordon and Breach,Yvendon,1993,17:77-82.
Non-Lipschitz stochastic differential equations driven by fractional Brownian
Ran Qikang
(School of Mathematics,Shanghai University of Finance and Economics,Shanghai200433,China)
In this paper,we discuss the existence and uniqueness of a class of non-Lipschitzd stochastic differential equations driven by fractional Brownian motion with Hurst parameterSo far,there are several ways to define stochastic integrals with respect to FBM.In this paper,we define stochastic integrals with respect to FBM as a generalized Stieltjes integral.We give a theorem of existence and uniqueness for SDE with coefficients allowed to have a non-Lipschitzd growth.
fractional Brownian motio,generalized Stieltjes integral, non-Lipschitz stochastic differential equation,adapted solution
O211.63
A
1008-5513(2016)06-0551-11
10.3969/j.issn.1008-5513.2016.06.001
2016-09-06.
国家自然科学基金(11601306).
冉启康(1964-),博士,教授,研究方向:随机分析.
2010 MSC:60H10,60H05
