在役钢筋混凝土梁桥极限承载力简化分析方法

张世春，朱劲松,2

（1.天津大学 建筑工程学院，天津 300072；2.天津大学 滨海土木工程结构与安全教育部重点实验室，天津 300072）

在役钢筋混凝土梁桥极限承载力简化分析方法

张世春1，朱劲松1,2

（1.天津大学 建筑工程学院，天津 300072；2.天津大学 滨海土木工程结构与安全教育部重点实验室，天津 300072）

针对目前应用较为广泛的钢筋混凝土梁桥，提出了基于混凝土梁单元-刚臂元-弹簧单元-钢筋单元体系的ANSYS有限元非线性分析模型．并以量大面广的钢筋混凝土简支T型梁桥为例，利用该有限元非线性分析模型对影响其极限承载力的各个参数进行了分析研究，以此推导出了此类简支梁桥的极限承载力公式．最后通过一些实桥分析，对比ANSYS与推导公式的计算结果，验证了该公式的可靠性．

钢筋混凝土；T型梁桥；极限承载力；非线性分析；公式推导

0 引言

钢筋混凝土桥梁是当今世界应用最为广泛的桥梁结构之一．长期使用以来，人们逐渐意识到钢筋混凝土桥梁存在着严重的承载力退化问题．而我国大部分桥梁建于上个世纪80年代以前，由于材料的长期退化，目前承载力已明显下降，危桥逐渐增多．及时对此类桥梁进行承载力评估已成为一项刻不容缓的工作，必须积极开展相关的研究并付诸实践．在承载力评估当中，桥梁结构的极限承载力评估较之设计承载力而言，往往更具有现实意义．这是因为结构设计计算针对的是单个构件，且采用的是简化的理想弹性力学模型，这都与实际桥梁的受力行为有所不同．而以结构为对象的极限承载力，只能是以结构完全丧失刚度为标志[1]．

目前，国内外已有不少学者针对在役混凝土桥梁极限承载力问题进行了相关研究，主要采用非线性有限元分析模型．Andrea Dall'Asta等[2]基于有限变形理论推导出小应变和中等转动理论，提出了一个完整考虑几何和材料非线性的分析模型；AshrafAyoub[3]采用梁单元、钢束单元和连接单元，提出了一种考虑粘结滑移、摩擦力和锚固损失的非线性有限元模型；HelderSousa等[4]则在非线性分析中考虑了混凝土强度和弹性模量随时间的变化；朱劲松等[5]针对钢筋混凝土梁桥，提出了基于平面应力单元-弹簧单元-桁架单元体系的二维有限元非线性分析模型；叶见曙等[6]针对预应力混凝土多T梁桥，基于实体退化壳单元理论，考虑材料非线性效应，研究了多T梁桥极限承载力的计算方法；吴光宇等[1]针对大跨预应力混凝土桥梁极限承载力的计算问题，提出了建立在三维实体退化虚拟层合单元理论基础上同时考虑结构双非线性的空间分析计算方法．国内外虽然已在在役混凝土桥梁极限承载力方面做了不少研究，但均需要通过有限元非线性分析来获得桥梁的极限承载力，这种方法较为复杂，适用人群较为局限而不易广泛应用．

本文旨在寻找求解极限承载力的简便方法，以目前量大面广的钢筋混凝土简支T型梁桥为例，利用有限元非线性分析模型对影响其极限承载力的参数进行分析研究，找出极限承载力与其截面尺寸、配筋情况以及跨径等的关系，从而推导出钢筋混凝土简支T型梁桥的极限承载力快速计算公式，并通过实桥算例验证了本文所提公式的可靠性．

1 材料本构模型

1.1 混凝土本构模型

随着龄期增长，混凝土与酸性气体发生反应而造成碳化．混凝土碳化后，其抗压强度有所增加，但总体而言，对抗弯承载力的影响不大[7]，故而不考虑混凝土抗压强度的变化．混凝土本构关系上升段采用GB50010-2002模型，下降段采用Hongnestad模型[8]：

1.2 锈蚀钢筋本构模型

钢筋锈蚀是导致桥梁承载力降低的主要因素之一．钢筋锈蚀后，其屈服强度有所减小，但钢筋弹性模量基本不变[9]，考虑锈蚀影响对钢筋理想弹塑性本构关系做如下修正：

1.3 锈蚀钢筋/混凝土粘结滑移模型

钢筋与混凝土之间拥有足够的粘结强度是两者得以共同工作的基础，但由于钢筋锈蚀，使得钢筋与混凝土之间的粘结强度显著降低，导致钢筋在较小的应力下便能产生较大的滑移量，因而对其影响应予以考虑．为此，徐善华等[10]提出了粘结强度锈蚀影响系数，得出锈蚀钢筋粘结滑移公式：

图1 混凝土应力-应变曲线Fig.1 Stress-strain constitutive curveof concrete

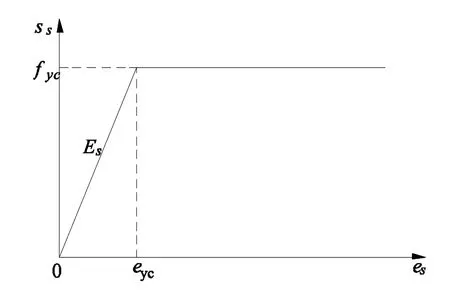
图2 钢筋应力-应变曲线Fig.2 Stress-strain constitutive curveof rebar

式中： 为粘结强度，MPa；0为未锈蚀钢筋的粘结强度，MPa，按下式计算：

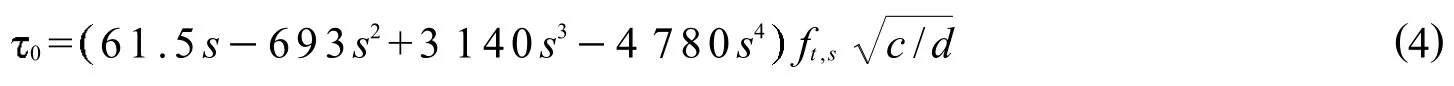
式中：s为滑移距离（mm）；ft,s为混凝土劈裂抗拉强度（MPa）；c为混凝土保护层厚度（mm）；d为钢筋直径（mm）．其粘结滑移曲线如图3所示．

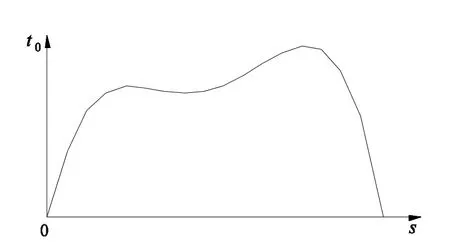
图3 未锈蚀钢筋/混凝土粘结滑移曲线Fig.3 Curveof bond and slip between rebar w ithoutcorrosion and concrete

式 (3)中， 为粘结强度锈蚀影响系数，按下式计算：

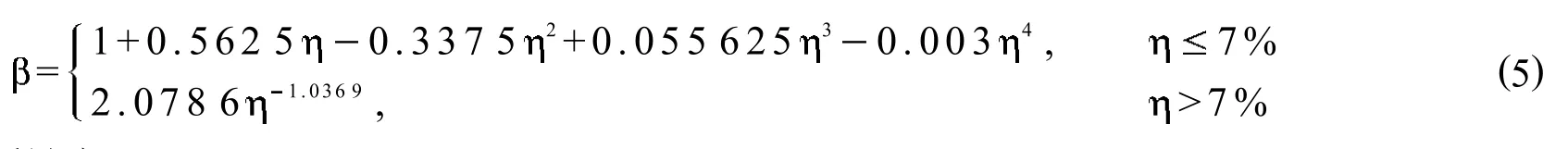
2 有限元建模方法

采用通用有限元软件ANSYS建立结构有限元模型，进而对结构进行整体非线性分析．一般而言，三维实体模型的计算结果相对精确，但其计算量也相对较大，因而更适用于局部分析．对于钢筋混凝土梁桥的整体非线性分析，采用基于梁单元-刚臂元-弹簧单元-钢筋单元体系的空间梁格模型，如图4所示．

图4 非线性有限元模型Fig.4 Nonliner finiteelementmodel

混凝土梁采用3D梁单元beam189模拟，考虑剪切变形影响，其本构关系采用多线性随动强化模型 KINH；纵梁之间采用虚梁连接，即不考虑虚梁自重，对于T型梁桥，虚梁梁高取翼板边缘厚度；钢筋采用3D杆单元link8模拟，通过改变单元截面和强度条件来模拟不同锈蚀情况下的钢筋截面面积和钢筋强度，其本构关系采用双线性随动强化模型BKIN．

在支座处建立支座节点，与对应梁节点之间采用刚臂连接，刚臂采用3D梁单元beam4模拟，其弹性模量E取1000Ec；混凝土梁与钢筋之间的连接如图4所示，节点①为混凝土梁单元上一点，节点②与钢筋节点③重合，节点①、②之间采用刚臂连接，节点②、③之间采用非线性弹簧单元连接，以模拟钢筋/混凝土粘结滑移，其沿钢筋纵向的荷载-位移关系如下式所示：

式中：F为粘结力（N）；n为同一高度处的钢筋数量；dc为锈蚀钢筋有效直径（mm）；lr为弹簧单元沿钢筋纵向的间距（mm）； 为式(3)中的粘结强度（MPa）．

3 极限承载力简化分析方法

3.1 基准模型

以某钢筋混凝土梁桥T梁截面尺寸为基准，见图5，布置两层受拉钢筋和一层受压钢筋，钢筋直径取20 mm，钢筋屈服强度取275 MPa，并采用C20混凝土，以此建立有限元基准模型，如图4所示．在此基础上，分别研究跨径l、梁高h、腹板宽b、翼缘板宽bf、翼缘板厚hf、受拉主筋面积As、受压主筋面积A's、混凝土抗压强度fck、钢筋屈服强度fyk、受拉主筋中心距as、受压主筋中心距a's、受拉主筋平均锈蚀率、受压主筋平均锈蚀率'、主梁数n以及车道数m对其极限承载力qu的影响．此处极限承载力qu为全载作用下单个车道所加载的最大均布荷载．

3.2 公式推导

3.2.1 参数分析

逐一改变各个参数数值，采用ANSYS进行有限元非线性分析，计算各参数值对应的极限承载力，并首先分析出单梁极限承载力q1u与各参数的对应关系，然后考虑主梁数n与车道数m对极限承载力qu的影响，从而进一步推导出极限承载力公式．目前，国内的钢筋混凝土简支T型梁桥跨径一般为8～20m；对应梁高一般为0.8～1.3 m；主梁间距一般为1.5～2.2 m；腹板厚度一般为160～240mm；翼板边缘厚度不小于80mm；横隔板一般设置于主梁1/2、1/4及支座处，高度约为梁高的3/4，宽度一般为120～200mm．各参数数值变动即以此为参照，单梁极限承载力q1u计算结果见图6．

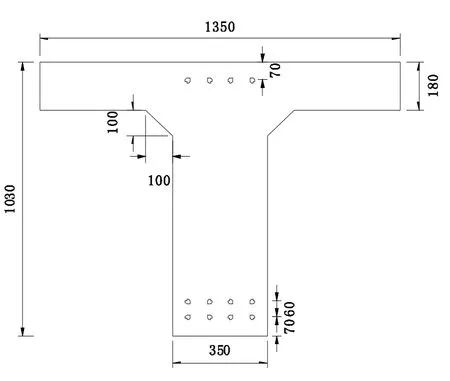
图5 基准T梁截面图（mm）Fig.5 Section diagram of reference T beam

3.2.2 单梁极限承载力

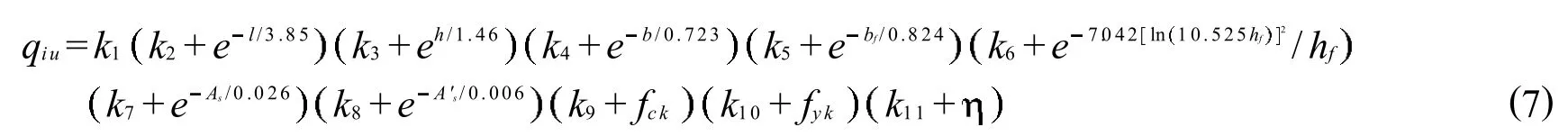
则单梁极限承载力与各参数的对应关系式可视为式 (7)的特殊情况，即若以参数l为变量，其余参数均按基准截面数据取为定值，则所得公式q1u=C k2+el/3.85应与公式q1u=24.996+1928.946el/3.85相同，据此可得k2，同理可求得k3～k11，在求得k2～k11后，可通过代入特殊值求解k1，具体求解结果见表1．

表1 系数k1～k11计算结果Tab.1 Calculation resultsof coefficient k1～k11

3.2.3 多梁极限承载力

前面推导出的仅仅是单梁极限承载力，而现实中的简支T型梁桥沿横向有多根主梁，因而需进一步研究多梁桥极限承载力qu与单梁极限承载力q1u之间的关系．此外，绝大多数的梁桥拥有两个车道或以上，车道数不同则荷载布置数量也不同（几个车道即施加几道均布荷载），故而也需对车道数的影响进行分析．本文以基准T梁截面的8 m跨径简支梁为例，对比分析了车道数为1、2、3时1、3、5、7、9片梁对应的极限承载力，具体计算结果见表2．

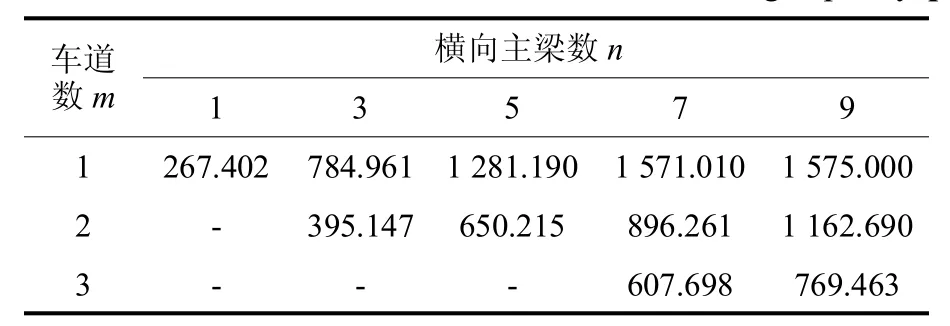
表2 极限承载力qu计算结果 kN/mTab.2 Calculation resultsof ultimate load bearing capacity qu

横向观察表2可以看出，当车道数为1时，1、3、5片梁对应的极限承载力比值为1∶2.936∶4.791，极限承载力qu与主梁数n近似呈正比例关系；当主梁数超过5片时，此时桥宽大于桥长，正比例关系不再成立，且7、9片梁对应的极限承载力几乎相同，即9片梁的最外侧两根梁几乎不受影响．说明一道均布荷载的影响范围有限，越往外侧影响越小，而当桥宽小于桥长时，每根梁均能得到充分利用，因而其极限承载力qu与主梁数n呈正比例关系．当车道数为2时，3、5、7、9片梁对应的极限承载力比值为3∶4.937∶6.805∶8.827，当车道数为3时，7、9片梁对应的极限承载力比值为7∶8.863，其极限承载力qu与主梁数n均近似呈正比例关系，原因在于此时桥宽小于2倍桥长，两道均布荷载即可使每根梁得到充分利用．

竖向观察表2不难发现，3、5片梁对应的极限承载力qu与车道数m近似成反比；车道数大于1时，7、9片梁对应的极限承载力qu亦与车道数m近似成反比，原因与上述相同，均取决于主梁是否得到充分利用．

根据上述分析，可以假设：

式中：f n为单车道下n梁极限承载力与单梁极限承载力的比值；g m 为单车道对应极限承载力与m车道

图6 单梁极限承载力q1u曲线图Fig.6 Curve chartof ultimate load bearing capacity q1uof singlebeam

对应极限承载力的比值，且f n与n、g m 与m均呈线性关系．

当车道数m为1时，根据表2中1、3、5片梁对应的数据求解f n，f n与n的具体关系见表3、图7．

f n与n的拟合曲线公式 (9)

根据表2中3、5片梁对应的数据亦可求解g m ，g m 与m的具体关系见表4．

表3 关系表Tab.3 Relationship betweenand n

表3 关系表Tab.3 Relationship betweenand n

n 1 3 5 f n 1 2 . 9 3 6 4 . 7 9 1

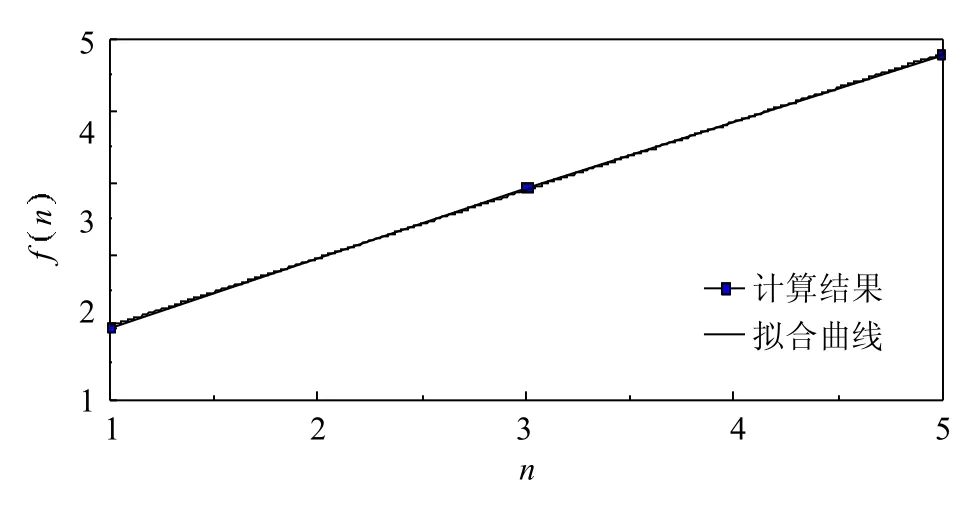
图7 f n与n的关系曲线Fig.7 Curveof relationship between f n and n

根据表4可以求得：

其中

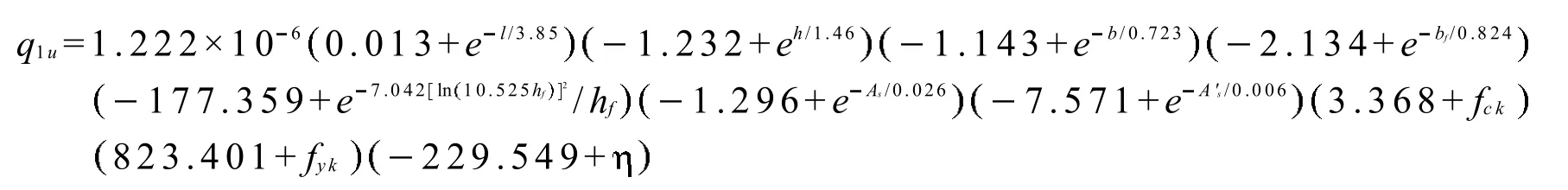
式中：l为跨径（m）；h为梁高（m）；b为腹板宽（m）；bf为翼缘板宽（m），取主梁横向间距；hf为翼缘板平均厚度（m）；As为受拉主筋初始面积（m2）；A's为受压主筋初始面积（m2）；fck为混凝土轴心抗压强度标准值（MPa）；fyk为钢筋初始屈服强度标准值（MPa）；为受拉主筋平均锈蚀率（%）．

表4 g-m关系表Tab.4 Relationship between gand m

表4 g-m关系表Tab.4 Relationship between gand m

m 1 2 g m 梁数n 3 1均值 梁数n 3 1 . 9 8 7 均值5 1 1 5 1 . 9 7 0 1 . 9 7 8

根据模型及分析可知，该公式仅当主梁翼板刚接且每片主梁均得到充分利用时适用，即：桥宽小于桥长时，适用于任何车道数；桥宽大于桥长而小于2倍桥长时，适用于两车道及以上．但对于实际简支梁桥，当桥宽大于桥长时，一般均有多条车道，因而该公式普遍适用于翼板刚接的钢筋混凝土简支T型梁桥．

3.3 分析验证

为了验证钢筋混凝土简支T型梁桥极限承载力快速计算公式的正确性，本文选取了一些实际简支T型梁桥，并假定钢筋锈蚀率均为0，采用ANSYS对其进行有限元非线性分析，计算各自极限承载力，并与公式计算结果进行对比．实桥截面尺寸、配筋情况等信息及对比验证结果见表5．

由表5可见，公式 (11)计算所得极限承载力与ANSYS分析计算所得极限承载力基本一致，除桥6、8误差达到 8%外，其余误差均在 5%以内，因而可以认为本文所推导的钢筋混凝土简支T型梁桥极限承载力快速计算公式在理论上正确可靠，可为在役钢筋混凝土简支T型梁桥极限承载力快速评估提供参考．

4 结论

本文旨在分析在役钢筋混凝土梁桥的极限承载力，并针对目前应用较为普遍的钢筋混凝土简支T型梁桥，以基于混凝土梁单元-刚臂元-弹簧单元-钢筋单元体系的ANSYS有限元非线性分析模型为计算手段，对影响钢筋混凝土简支T型梁桥极限承载力的各个参数进行了分析研究，以此推导出其极限承载力快速计算公式．并通过一些实桥分析，对比ANSYS与推导公式的计算结果，验证了该公式的可靠性．

具体结论如下：1）本文所推导公式可作为在役钢筋混凝土简支T型梁桥极限承载力的评估依据，且该公式计算较为方便，从而为此类桥梁的极限承载力评估提供了便利；2）单梁极限承载力与各参数基本呈非线性关系，且当各片主梁得到充分利用时，多梁极限承载力与主梁数呈正比；3）本文极限承载力快速计算公式的推导方法具有一定的可借鉴性，可根据该方法对其它类型梁桥的极限承载力进行研究．

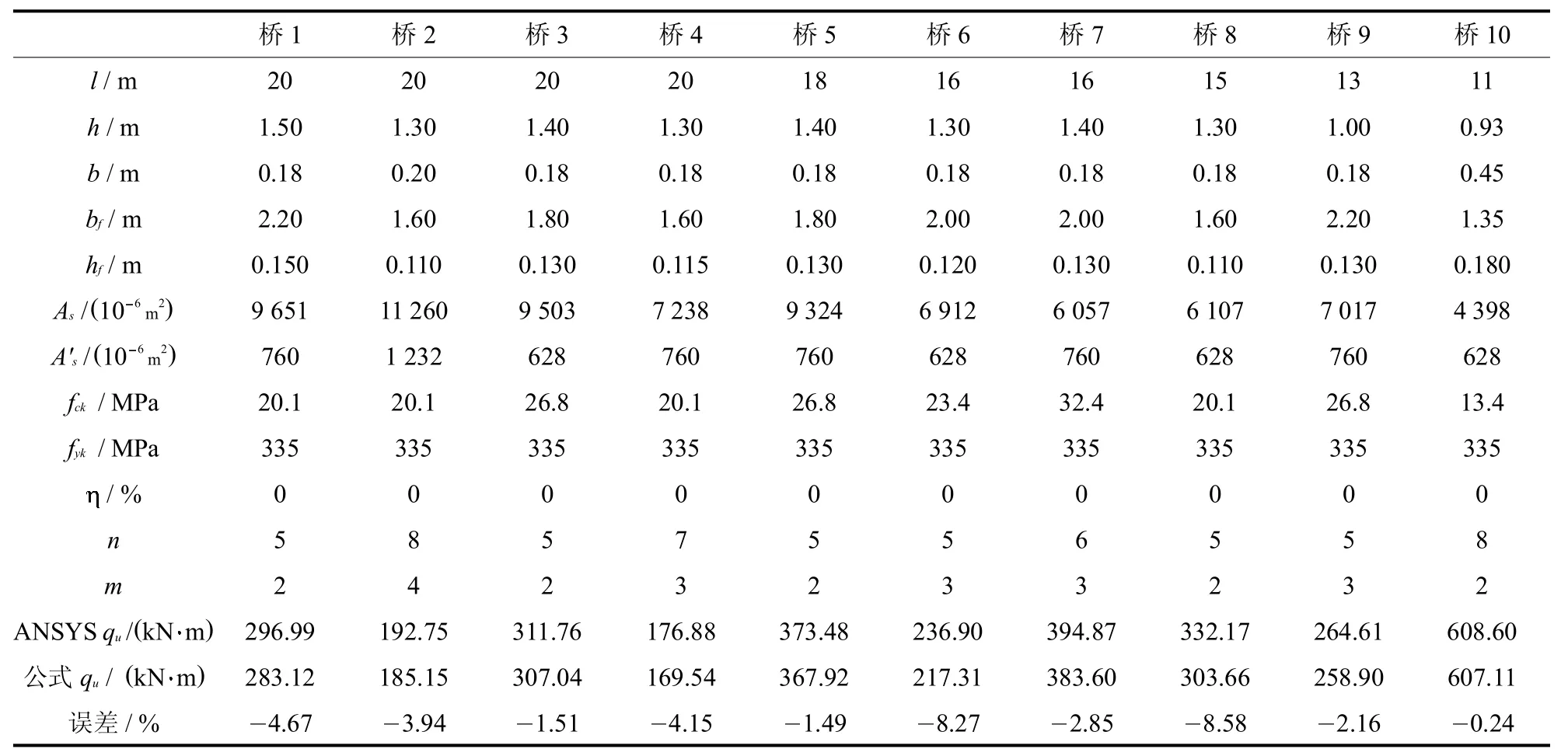
表5 实桥极限承载力验证结果Tab.5 Test resultsofultimatebearing capacity of realbridge

[1]吴光宇，杨升善，汪劲丰，等．大跨预应力混凝土桥梁极限承载力计算 [J]．南昌大学学报（理科版），2013，37（2）：198-204．

[2]AndreaDall'Asta，LauraRagni，A lessandro Zona．AnalyticalModel forGeometricandMaterialNonlinearAnalysisofExternally Prestressed Beams [J]．JEng Mech，2007，133：117-121．

[3]Ashraf Ayoub．Nonlinear Finite-ElementAnalysisof Posttensioned Concrete BridgeGirders[J]．JBridge Eng，2011，16：479-489．

[4]HelderSousa，João Bento，Joaquim Figueiras．Constructionassessmentand long-term predictionofprestressed concretebridgesbasedonmonitoring data[J]．Engineering Structure，2013，52：26-37．

[5]Zhu Jinsong，Gao Change．Probabilistic durability assessmentapproach of deteriorating RC bridges[J]．Journal of Southeast University(English Edition)，2011，27（1）：70-76．

[6]叶见曙，张剑，黄剑峰．预应力混凝土多T梁桥的极限承载力 [J]．东南大学学报（自然科学版），2009，39（1）：106-111．

[7]马广强．腐蚀与疲劳耦合作用下钢筋混凝土桥梁数值模拟方法研究 [D]．天津：天津大学，2010．

[8]王新敏．ANSYS工程结构数值分析 [M]．北京：人民交通出版社，2007．

[9]张伟平，商登峰，顾祥林．锈蚀钢筋应力-应变关系研究 [J]．同济大学学报，2006，34（5）：586-592．

[10]徐善华．混凝土结构退化模型与耐久性评估 [D]．西安：西安建筑科技大学，2003．

[责任编辑 杨 屹]

Simplified analysismethod forultimatebearing capacity ofexisting reinforced concrete girderbridges

ZHANG Shichun1，ZHU Jinsong1,2

(1.SchoolofCivilEngineering,Tianjin University,Tianjin300072,China;2.Key Laboratory ofCoastCivilStructureSafety(Tianjin University),M inistry of Education,Tianjin 300072,China)

For thew idely used reinforced concretegirderbridges,thispaperproposesan ANSYS finiteelementnonlinear analysismodelbased on the system of concretebeam element-rigid arm element-spring element-reinforced element.And taking thew idespread reinforced-concrete-simply supported-T beam bridge as an example,this paperanalyses the parameters thataffect its ultimate bearing capacity w ith this finite elementnonlinear analysismodel to derive the formula of ultimate bearing capacity of such bridges.Finally,the reliability of the formula is verified through the analysis of some realbridgesand comparing the calculation resultsof ANSYSand the formula.

reinforced concrete;T-beam bridge;ultimate bearing capacity;nonlinearanalysis;formula derivation

TP183；U448

A

1007-2373(2016)02-0096-08

10.14081/j.cnki.hgdxb.2016.02.017

2015-07-20

国家自然科学基金（51178305）；天津市应用基础与前沿技术研究计划（14JCYBJC21500）

张世春（1991-），男（汉族），硕士生．通讯作者：朱劲松（1975-），男（汉族），教授，博士，博士生导师．