弹性常数对液晶盒电容的影响
2017-01-04宋晓龙叶文江邢红玉刘小松
宋晓龙,叶文江,邢红玉,刘小松
(1.河北工业大学 理学院,天津 300401;2.天津大学 电子信息工程学院,天津 300072)
弹性常数对液晶盒电容的影响
宋晓龙1,2,叶文江1,邢红玉1,刘小松1
(1.河北工业大学 理学院,天津 300401;2.天津大学 电子信息工程学院,天津 300072)
液晶材料的弹性常数影响外加电压下液晶盒中液晶分子的取向排列,导致液晶盒电容发生变化.基于Frank弹性理论和变分原理,研究了扭曲向列相(TN)液晶盒的电容特性.采用差分迭代方法数值模拟计算得到不同扭曲弹性常数下TN盒约化电容随外加电压变化的曲线,由此分析了扭曲弹性常数k22对TN盒电容的影响.液晶盒电容的测量是确定液晶材料弹性常数k22的一种有效的方法.
液晶盒电容;向列相液晶;弹性常数;差分迭代方法
0 引言
众所周知,弹性常数是一个重要的液晶材料参数,直接影响液晶显示器件的阈值电压、响应时间、占空比等性能[1].因此,液晶材料弹性常数的研究对液晶材料属性的认识及液晶显示器件的优化具有十分重要的意义.
液晶材料的弹性常数可以通过电容法测量得到,其本质是液晶材料的弹性常数影响外加电压下液晶盒中液晶分子的取向排列.文献 [2-7]曾分析液晶盒电容特性,并给出了液晶盒电容随电压的变化曲线,由此得到液晶材料弹性常数电容法测量的理论分析.但是,他们主要讨论了展曲和弯曲弹性常数k11和k33对平行排列向列相(PAN)液晶盒或混合排列向列相(HAN)液晶盒电容的影响,而扭曲弹性常数k22的影响没有考虑.若要考虑k22的影响,需要研究扭曲向列相(TN)液晶盒的电容特性.基板表面对液晶的锚定对液晶盒电容有明显的影响[7],为了屏蔽基板锚定特性在分析弹性常数k22对TN液晶盒电容影响的负面作用,考虑强锚定情形.
基于Frank弹性理论和变分原理,得到外加一定电压强锚定TN液晶盒达到平衡时指向矢倾角、扭曲角和电压满足的微分方程;将差分代替微分可以得到上述3个变量的迭代格式;通过VisualFortran软件数值模拟得到不同扭曲弹性常数k22下TN液晶盒的c-U曲线,并由此分析了扭曲弹性常数k22对TN液晶盒电容的影响.
1 理论分析
强锚定扭曲向列相液晶盒结构如图1所示,液晶盒厚度为l,下玻璃基板处液晶分子沿x方向排列,上玻璃基板处液晶分子沿y方向排列.沿z方向外加一电压U作用在液晶盒上,当超过阈值电压时,均匀扭曲排列的液晶分子将产生形变,指向矢由倾角 和扭曲角 确定,且只是空间坐标z的函数.
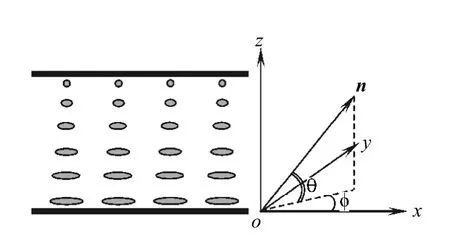
图1 扭曲向列相液晶盒结构及坐标系Fig.1 Structureof the twisted nematic liquid crystal celland theCartesian coordinate system
液晶盒看作是1个封闭系统,由液晶弹性理论可推理得到单位面积系统的自由能表达式为


将式 (1)分别代入方程 (2)~(4)可以得到系统达到平衡态时、 和U满足的方程为
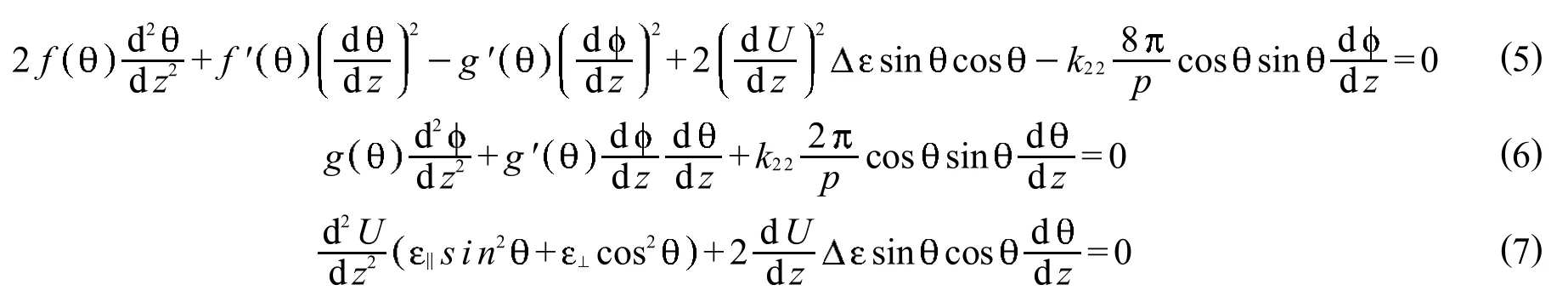
外加一定电压下达到平衡时, 和 在液晶盒内部的值是固定的,此时液晶盒约化电容为[4-7]

其中:c=C/C0,C0=S0/l为不加电压时TN液晶盒的电容,S为基板的面积;.
2 数值计算
在进行液晶指向矢和液晶盒电容数值计算时,将液晶盒均匀地分成N(N=100)个薄层,每1个薄层的厚度为h=l/N,液晶盒上下基板分别对应第N层和第1层.对于强锚定边界条件,上下基板处液晶分子的预倾角和预扭曲角都是固定的.第i个液晶子层的 、 和U差分格式为[10]

式 (9)代入方程 (5)~(7)可以得到系统达到平衡态时 、 和U满足的迭代方程:
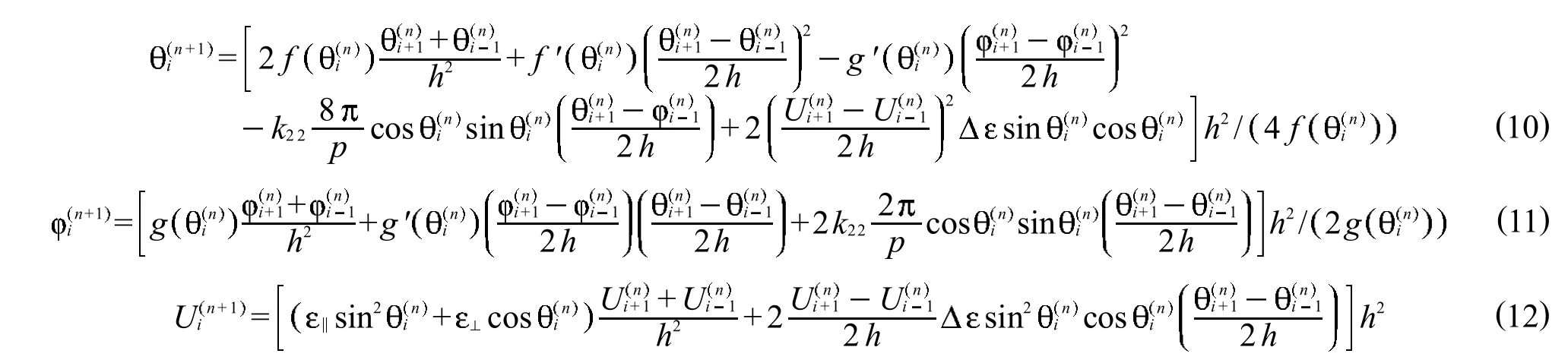
这样就得到了1组差分迭代的方程组,然后利用FORTRAN软件编程就可以模拟出TN型液晶盒的指向矢分布,进而代入到方程(8)中,可计算得到液晶盒的电容值,改变不同的电压对应不同的电容,利用Origin软件绘制出相应的c-U曲线图.
3 计算结果
对于 TN型液晶盒,其主要参数有 k11=9.0 pN,k22=7.0 pN,k33=16.8 pN, =7.30, =3.60,考虑液晶盒预倾角度为2°的情况,液晶指向矢倾角和扭曲角分布如图2所示.
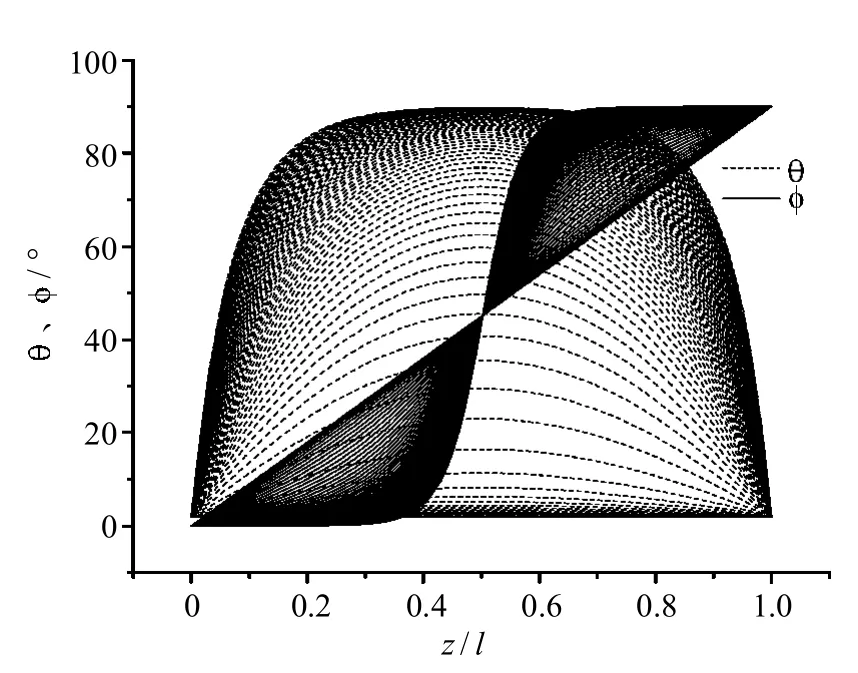
图2 不同电压下液晶指向矢分布Fig.2 Distribution of liquid crystaldirector w ith differentvoltages
可以看出:在强锚定边界条件下,对于TN液晶盒,在不同的电场作用下,液晶盒中指向矢倾角分布(弓形曲线)相对层中心对称,在低电场下近似于正弦曲线,而在高电场下变为方形;扭曲角分布(对角曲线)在外加电场增加到使中间层倾角超过约40°之前一直保持均匀.
与PAN液晶盒相比,TN液晶盒中对液晶分子影响较大的是扭曲弹性常数k22,因此在研究弹性常数对液晶盒电容影响的过程中,主要考虑k22的变化对电容值的影响.计算中液晶材料的展曲和弯曲弹性常数及介电常数与计算指向矢分布时相同,而扭曲弹性常数k22的取值为k22=k×k11,其中k为比例系数,弹性常数取不同值k=0.5、0.6、0.7、0.8、0.9、1.0时得到了TN液晶盒的c-U曲线,如图3所示.
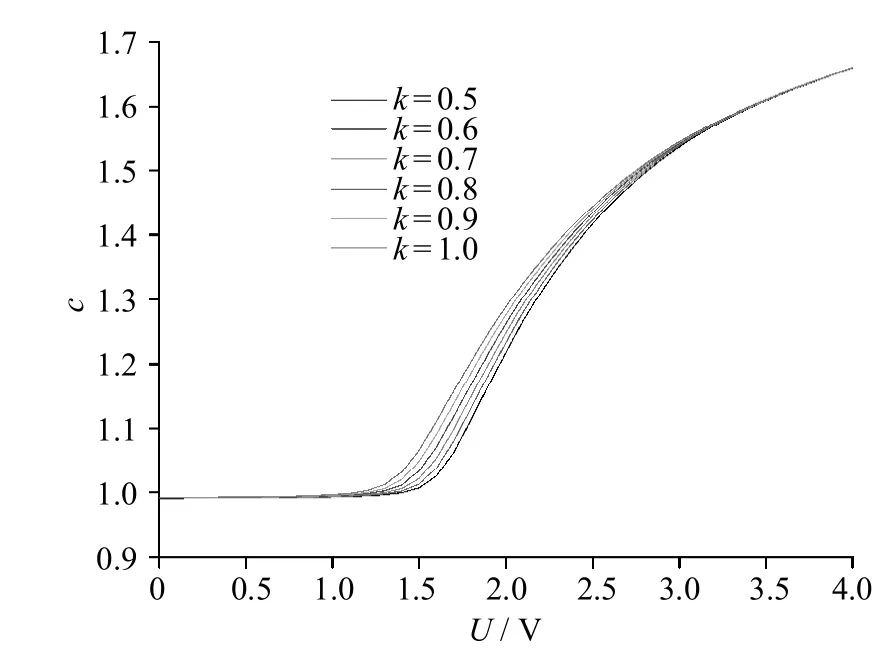
图3 预倾角为2°时不同弹性常数下液晶盒约化电容随驱动电压的变化Fig.3 Variation of reduced capacitanceof liquid crystal cellwith driven voltage for different elastic constantsw ith pre-tiltangle2°
由图3可以看出:1)液晶盒的电容是随驱动电压的改变而不断变化的,而且随着电压U的增大,液晶盒的电容值也在不断增大,而且变化得比较明显;2)图中曲线开始处于平行状态,这是由于液晶盒阈值电压的存在,当驱动电压小于阈值电压时,液晶盒的指向矢分布不发生变化,此时液晶盒的电容值也保持不变;3)在较低电压1.2~3.5 V时,液晶盒的电容随弹性常数的增大而增大,在较高电压(大于3.5V)时,弹性常数的变化对液晶盒的电容值没有明显影响;4)无论液晶盒的弹性常数取何值,随着所加电压的增大,液晶盒的指向矢分布都是稳定的,因此,在图线中可以发现,电容的变化逐渐平缓并且在达到一定电压时不再变化,趋于某一恒定值.
在上面的研究中,选取的液晶盒预倾角度为2°,为了考虑预倾角的改变引起的变化,选取预倾角度为0°和4°,得到的液晶盒c-U曲线如图4和图5所示.
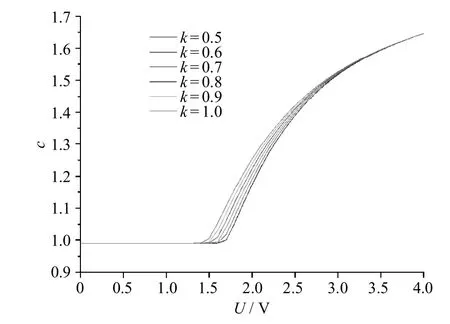
图4 预倾角为0°时不同弹性常数下液晶盒约化电容随驱动电压的变化Fig.4 Variation of reduced capacitanceof liquid crystalcell w ith driven voltage for differentelastic constantsw ith pre-tiltangle0°

图5 预倾角为4°时不同弹性常数下液晶盒约化电容随驱动电压的变化Fig.5 Variation of reduced capacitanceof liquid crystalcell w ith driven voltage for differentelastic constantsw ith pre-tiltangle4°
对比图3、图4和图5可以看出:1)无论预倾角为0°、2°或4°时,液晶盒的c-U曲线变化趋势大体相同,当液晶盒的电容值开始变化时,在较低电压下,液晶盒的电容随弹性常数的增大而增大,在较高电压,弹性常数的变化对液晶盒的电容值没有明显影响;2)对应图3、图4和图5,使得液晶盒电容变化的最小驱动电压为分别为1.2 V左右、1.5 V左右和1.0 V左右,这就表明液晶盒的预倾角越小,使得液晶盒中液晶分子发生形变的阈值电压就会越大;3)在较低电压(1.8V)下,图4中液晶盒约化电容随驱动电压的变化趋势相对明显,表明液晶盒的预倾角越小,弹性常数对液晶盒电容值的影响就越大.
4 结论
分析处于强锚定条件下的TN型液晶盒,基于液晶弹性理论和变分原理,得到了TN型液晶盒的平衡态方程,并利用差分格式得到了 、 和U的迭代方程,然后利用FORTRAN软件进行数值模拟计算,给出了TN液晶盒的指向矢分布及c-U曲线.其次,为了考虑TN液晶盒在不同预倾角度下约化电容随驱动电压的变化,分别选取了预倾角为0°、2°和4°,绘制出相应的c-U曲线.通过比较得到的c-U曲线可以看出随扭曲弹性常数和预倾角增加,使TN盒电容发生变化的电压逐渐减小,电容值达到恒定的电压值基本保持为3V,并且TN盒电容的电压可调范围逐渐增大.本文得出的结论将为后期使用电容法测量液晶材料扭曲弹性系数k22提供了理论参考.
[1]Yang D K,Wu ST.Fundamentalsof Liquid CrystalDevices[M].Chichester:JohnWiley&Sons Ltd,2006.
[2]StephenWilliam Morris.Measurementsof theelastic constantsof a liquid crystal[D].Vancouver:University of British Columbia,1985.
[3]孔祥建,荆海,黄霞,等.一种改进的C-V方法对向列相液晶弹性常数k11、k33测量的理论研究 [J].液晶与显示,2007,22(5):587-590.
[4]崔文静,邢红玉,张艳君,等.挠曲电效应对向列相液晶盒电容的影响 [J].数值计算与计算机应用,2012,33(2):142-150.
[5]崔文静,邢红玉,张艳君,等.混合排列向列相液晶盒电容特性研究 [J].液晶与显示,2012,27(5):608-612.
[6]崔文静,邢红玉,叶文江,等.液晶可调电容器的研究 [J].液晶与显示,2013,28(2):173-178.
[7]叶文江,刘小松,宋晓龙,等.基板锚定特性对液晶电容的影响 [J].液晶与显示,2014,29(5):686-691.
[8]王谦,何赛灵.液晶指向矢分布的模拟和比较研究 [J].物理学报,2001,50(5):926-932.
[9]谢毓章.凝聚态物理学丛书:液晶物理学 [M].北京:科学出版社,1998.
[10]张志东,叶文江,邢红玉.液晶盒中挠曲电效应的计算 [J].计算物理,2004,21(2):156-160.
[责任编辑 杨 屹]
Influenceofelastic constantson the capacitanceof liquid crystalcell
SONG Xiaolong1,2,YEWenjiang1,XINGHongyu1,LIU Xiaosong1
(1.SchoolofSciences,HebeiUniversity of Technology,Tianjin300401,China;2.SchoolofElectronicsand Information Engineering, Tianjin University,Tianjin 300072,China)
The elastic constants of liquid crystalhave an effecton the orientation of liquid crystalmoleculesw ith an externalapplied voltage,which results in a change of the capacitance of liquid crystal cell.Based on Frank elastic theory and variationalprinciple,the capacitancecharacteristicsofa tw isted nematic(TN)liquid crystalcellis researched.Using the difference iterativemethod,the reduced capacitance-voltage curveof the TN cell fordifferent tw isted elastic constant isobtained by thenumericalsimulation.Then,weanalyze the influence of tw isted elastic constantk22on the capacitance of liquid crystalcell.Thus,themeasurementofcapacitanceof liquid crystalcellisakind ofeffectivemethod to determ ine the tw isted elastic constantk22of liquid crystal.
capacitance of liquid crystal cell;nematic liquid crystal;elastic constant;difference iterativemethod
O753.2
A
1007-2373(2016)02-0092-04
10.14081/j.cnki.hgdxb.2016.02.016
2014-12-23
河北省自然科学基金(A2014202123);河北省教育厅项目(QN2014130);河北工业大学大学生创新创业训练计划(201310080001)河北工业大学教育教学改革研究项目(201502023)
宋晓龙(1993-),男(汉族),硕士生.通讯作者:叶文江(1976-),男(汉族),副教授.
数字出版日期:2016-04-18 数字出版网址:http://www.cnki.net/kcms/detail/13.1208.T.20160418.0928.002.htm l
