椭圆形内伸自紧密封高压快开人孔可行性分析

高炳军，孙少南，杜招鑫，李凯丽

（河北工业大学 化工学院，天津 300130）

椭圆形内伸自紧密封高压快开人孔可行性分析

高炳军，孙少南，杜招鑫，李凯丽

（河北工业大学 化工学院，天津 300130）

椭圆形自紧密封快开人孔用于高压疲劳设备超出现有设计标准范围，对其进行可行性分析十分必要．采用有限元方法对椭圆形自紧密封快开人孔结构进行分析计算，考察了人孔内伸长度对密封性能的影响，发现在最佳内伸长度下，椭圆形垫片上、下表面的接触压力分布最为均匀，且平均接触压力值较大，具有良好的密封效果，可满足密封要求．同时在合理的结构参数下，椭圆形人孔可满足抗垮塌、安定性、抗疲劳以及稳定性要求．研究表明，椭圆形内伸自紧密封快开人孔可用于高压疲劳设备．

高压；椭圆形人孔；内伸；自紧密封；疲劳；分析设计

0 引言

椭圆形内伸自紧人孔在锅炉汽包等中低压设备中已有应用，与外伸式人孔结构相比，椭圆内伸人孔装置有如下优点：不需设置外部连接法兰，外伸长度减少，改善空间结构，可降低设备投资；凭借介质压力形成密封，降低螺栓预紧力；方便密封元件的拆装等[1-2]．JB/T 2190-1993中对于椭圆形人孔结构有详细介绍，但其仅适用于压力低于3.82 MPa的设备．在某些高压快开设备中，由于工艺需要，也需采用椭圆形内伸人孔结构，依靠介质高压形成自紧密封．但椭圆形开孔由于其非轴对称特性，会导致人孔筒节上同时存在轴向应力、周向应力和径向弯曲应力，使得密封部位压紧力不均匀，影响密封效果[3]．人孔筒节与容器连接区会存在较大的应力集中，且在椭圆长轴两端应力最大，导致连接部分极易发生破坏[4]．本文采用有限元法对椭圆形内伸自紧人孔的密封性能、极限承载能力、安定性以及抗疲劳特性等进行评价，考察该结构在高压设备中使用的可行性．

1 有限元计算模型

某盛装压缩空气的高压储气罐，设计压力P=25MPa，循环载荷0～25MPa，循环次数2 200次，设计温度T=50℃，材料为Q345R（正火），弹性模量E=1.97×105MPa，泊松比=0.3，设计应力强度Sm=181MPa．应用分析设计方法对球封头内径进行优化[5]，确定最佳封头内径R2=583mm，厚度T2=45mm．筒体直径D1=1 100mm，筒体壁厚T1=88mm，人孔长轴a=200mm，b=170mm，壁厚T3=40mm垫片采用金属平垫片，材料为软黄铜,弹性模量E=1.17×105MPa，泊松比=0.3．建立1/4实体模型进行有限元计算，有限元模型如图1所示，考虑边缘应力衰减长度[6]，取有限元模型中筒体长度L=1 000mm．

采用SOLID185单元进行网格剖分，垫片上下表面设置接触对，考察垫片上下表面的接触压力分布，借此来评价结构的密封性能，其中，目标单元采用 TARGE170，接触单元采用 CONTA174，接触摩擦系数取0.3．在筒体、封头、人孔以及平盖等于介质接触的表面施加均布载荷25 MPa；筒体下端面约束轴向位移，两个对称面施加对称约束．网格剖分及载荷约束状况如图2所示．

图1 有限元模型Fig.1 The finiteelementmodel

图2 网格剖分及边界条件Fig.2 Meshing and boundary conditions

2 密封性能评价

2.1 垫片表面接触压力分布规律

内伸长度为120 mm时垫片上、下表面的接触压力分布云图如图3、图4所示．沿垫片径向由外向内有13个节点，沿周向0°～90°有91个节点．云图中看出垫片上表面内侧接触压力较大，向外逐渐减小，外侧有最小值，接触压力变化平缓．垫片下表面接触压力在垫片0°～20°外侧处有最小值，70°～90°内侧处有最大值．沿垫片周向求取接触压力平均值，作出平均接触压力沿垫片径向的变化规律如图5．外壁面处的接触压力值较小，其余部分的接触压力均在100MPa以上，文献指出只要接触压力值峰值大于内部介质压力，就可以保证垫片的密封性能[7]，因此结构可以保证良好的密封效果．

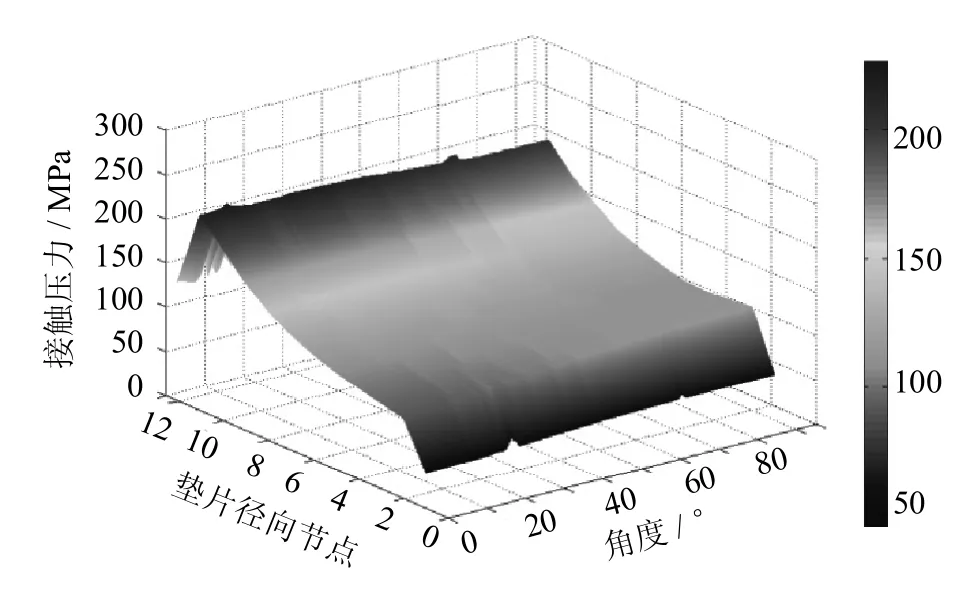
图3 垫片上表面接触压力分布Fig.3 Thecontactpressuredistributionofgasketuppersurface

图4 垫片下表面接触压力分布Fig.4 The contactpressure distribution of gasket lowersurface

沿垫片径向求平均值，作出平均接触压力沿垫片周向的分布规律如图6所示．上表面接触压力无明显变化，基本维持在130MPa左右．下表面接触压力随着角度的增加逐渐增长，在0°～15°和75°～90°范围内增速较为缓慢，在15°～75°范围内增长趋势较为明显，0°处有接触压力最小值，此时接触压力为101 MPa．由周向分布结果亦能评定此结构能保证较好的密封效果．

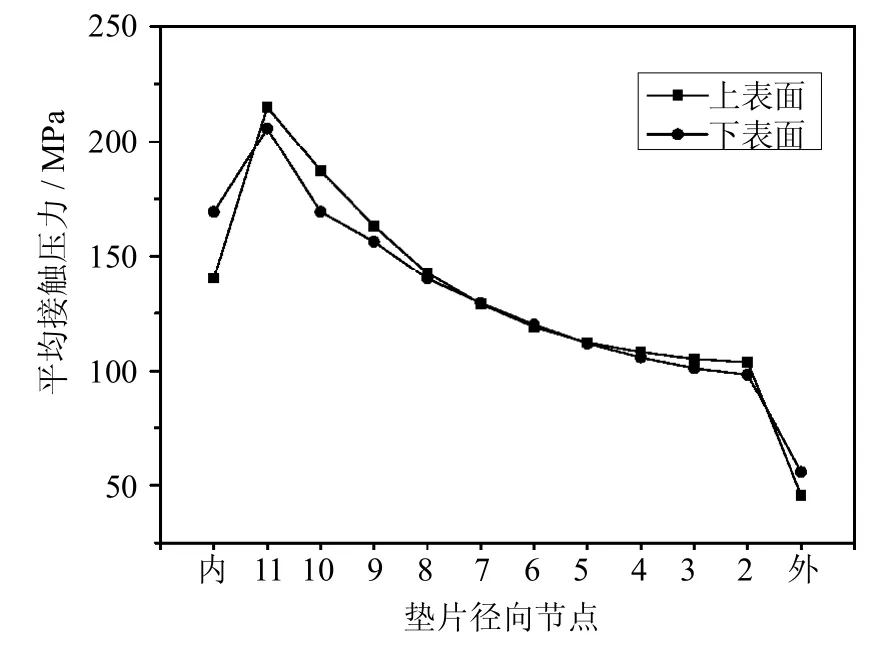
图5 垫片表面径向接触压力分布规律Fig.5 The contactpressure distribution along the radial direction of gasketsurface

图6 垫片表面周向接触压力分布规律Fig.6 Thecontactpressuredistributionalong thecircum ferential direction of gasketsurface

2.2 人孔内伸长度对密封性能的影响

椭圆形人孔的内伸部分在容器内部属于受压元件，平盖和筒节在压力作用下，会发生一定的翘曲变形，使得压紧面处接触压力分布不均匀，位移夸大云图如图7所示；人孔的内伸长度对压紧端面变形量有着较大的影响，因此需对于人孔内伸长度进行优化．改变内伸长度，分别提取垫片上、下表面所有节点的接触压力，首先求取接触压力的周向平均值，再求取其平均值、最大值和最小值，以此研究内伸长度对密封性能的影响，图8、图9分别为垫片上、下表面接触压力在不同内伸长度下的分布规律．

图7 位移云图Fig.7 Displacementcontour

图8 不同内伸长度垫片上表面接触压力Fig.8 The contactpressure distributionof gasketupper surface w ith diffrrent in-truding length

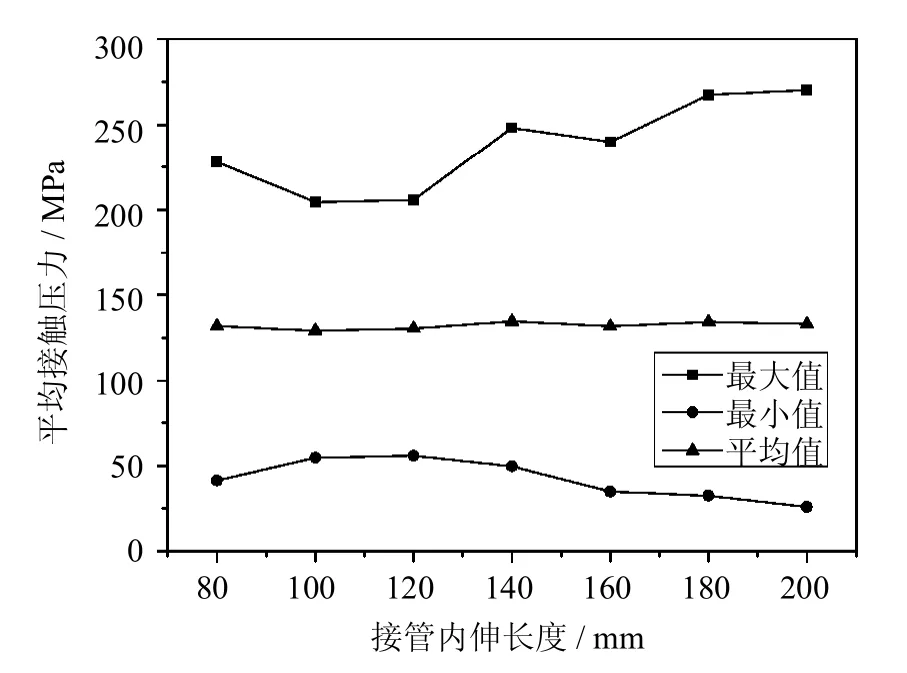
图9 不同内伸长度垫片下表面接触压力Fig.9 The contactpressure distribution of gasketlower surface w ith diffrrent in-truding length

平均接触压力在不同的内伸长度下较为接近，但最大值和最小值具有较大幅度的波动．随着内伸长度的增加，最大接触压力先降后增，内伸长度为120mm时有最小值，200mm时有最大值；最小接触压力波动先增后减，在160～200 mm范围内有着较小的值．计算可知，在内伸长度100～120 mm时，最大、最小接触压力差较小，垫片表面接触压力分布均匀，密封效果较好．内伸长度在160 mm以上时，最大接触压力虽然较大，但最小接触压力值偏小，此时接触压力分布欠均匀，相对于120mm时密封效果较差．从提取的节点接触压力数据发现，当内伸长度大于140mm时，垫片上表面最外侧接触压力为0；当内伸长度大于180mm时，垫片下表面最外侧处的接触压力也出现0值，说明压紧结构变形较大，不利于结构的密封．

从不同内伸长度下垫片上、下表面接触压力分布状况可以看出，当内伸长度为120mm时，具有最佳的密封效果．

3 强度评价

依据JB 4732-1995《钢制压力容器-分析设计标准》进行应力分类，封头人孔连接处一次局部薄膜应力及一次加二次应力需要进行评定．由于球形封头的椭圆形人孔是一种非轴对称结构，不便直接对一次局部薄膜应力进行应力强度评定，JB 4732-1995规定当给定载荷不超过结构塑性极限载荷的2/3时，即认为结构是满足抗垮塌要求[8]，故采用极限载荷法评价结构的抗垮塌性能．一次加二次应力仍根据安定性准则按应力分类法进行评定．此外，压缩空气罐存在交变载荷，需对结构进行疲劳强度评定．

3.1 抗垮塌评价

取材料的屈服极限ReL=325MPa，并给定一较大的压力值P=100MPa进行大变形非线性求解．内伸长度为120mm时，应变强度云图如图10所示，最大应变强度点位于人孔与封头连接区椭圆长轴外壁面处．该点应变强度与载荷的对应关系如图11所示，数值计算不收敛载荷即结构的塑性极限载荷为Plim=44.792MPa，许用载荷为

因此，该结构在工作压力下不会发生垮塌破坏．

图10 应变强度Fig.10 Strain intensity

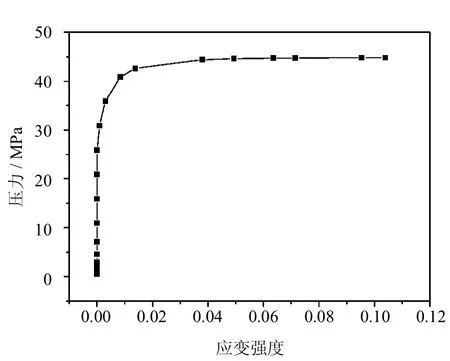
图11 载荷-应变强度曲线Fig.11 The load and strain intensity curve

3.2 安定性评价

依据线性化处理方法对封头人孔连接部位的一次加二次应力强度进行评定．评定准则为

由有限元计算应力云图可以看出在连接区人孔长轴内壁面处应力强度最大，封头内壁面处应力强度也较大，在此两处位置处定义两条应力评定线L1和L2如图12所示．

当内伸长度为120mm时，对于路径L1，PL+Pb+Q=411.4MPa，对于路径L2，PL+Pb+Q=225.2MPa，允许值为543MPa，均满足式 (2)要求．

3.3 疲劳强度评价

在内压作用下，最大应力强度点发生在封头人孔连接区人孔长轴内壁面处，应力强度值为423.107MPa，如图12所示．对应应力强度幅为211.55MPa，允许循环次数N=14 820次，可满足工作循环数2 200次的要求．

4 稳定性评价

由于人孔内伸部分承受外压，有必要进行稳定性评价，对内伸长度为120mm的椭圆形筒节施加25MPa的外压进行特征值屈曲分析，失稳模态如图13所示，屈曲载荷系数为147.03MPa，临界压力为3675.8MPa，利用统一屈曲模态法对结构进行大变形屈曲分析，临界压力为2 657.6MPa，可见结构的稳定性不成问题．

图12 应力强度Fig.12 Stress intensity

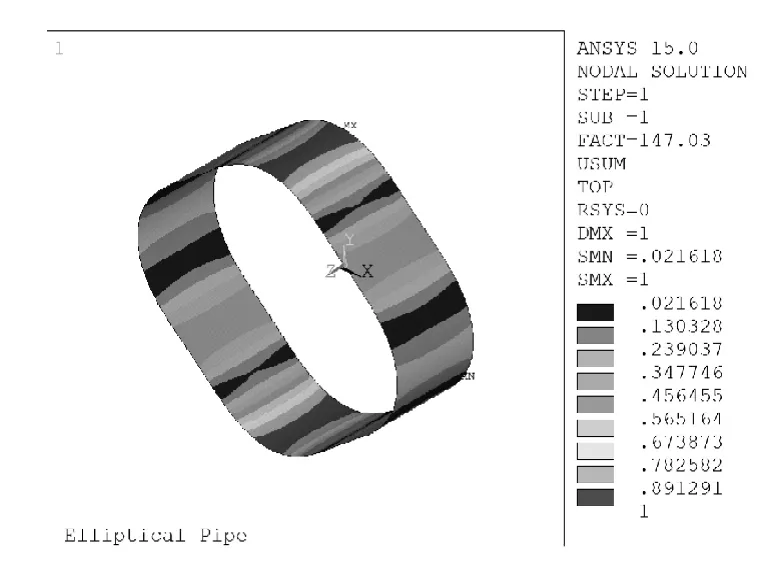
图13 椭圆管失稳模态Fig.13 Bucklingmodeof elliptical tube

5 结论

对某高压压缩空气罐的椭圆形内伸自紧人孔进行了有限元计算，考察了人孔内伸长度对自紧密封效果的影响，发现在最佳人孔内伸长度下，椭圆形垫片上下表面的接触压力分布最为均匀，且平均接触压力值较大，具有最佳的密封效果．同时合理的结构参数下，椭圆形人孔可满足抗垮塌、安定性、抗疲劳以及稳定性要求．因此，椭圆形人孔应用于高压疲劳设备是可行的．

[1]齐昆，张驰群．椭圆形内开自紧式人孔的强度计算方法探究 [J]．化工设备与管道，2012，49（1）：15-17，32．

[2]吴国荣．压力容器内置椭圆人孔的设计 [J]．石油化工设备，1987，16（4）：18-24．

[3]甄志强，龙华，王彩虹．椭圆形人孔强度和刚度的有限元分析 [J]．机械，2009，36（4）：28-30．

[4]马新旭，叶伟文．CAE在压力容器检验中的应用 [J]．中国特种设备安全，2011，27（6）：21-24．

[5]杜雅飞，崔静，高炳军．加氢反应器球形封头内径的确定 [C]//2004年中国机械工程学会年会，2004：1．

[6]陆明万，徐鸿．分析设计中若干重要问题的讨论（一）[J]．压力容器，2006，23（1）：15-19．

[7]陈国定，Haiser H，HaasW，等．O形密封圈的有限元力学分析 [J]．机械科学与技术，2000，19（5）：740-741，744．

[8]JB 4732-1995，钢制压力容器—分析设计标准（2005年确认）[S]．

[责任编辑 田 丰 夏红梅]

A study on the feasibility elliptical intruding and self-sealing quick-openingmanholeunderhigh-pressure

GAO Bingjun，SUN Shaonan，DU Zhaoxin，LIKaili

(Schoolof Chem ical Engineering,HebeiUniversity of Technology,Tianjin 300130,China)

Since The elliptical intruding and self-sealing quick-openingmanhole used in fatigue equipmentunder highpressure isbeyond theexisting design standard,the feasibility study isnecessary.The finiteelementmethod hasbeenused to analyse the sealing capability by changing the intruding length.The results show that,w ith the best intruding length, the contactpressureon gasketsurface isevenly distributed and theaverage contactpressure is relatively higher,which can ensure thisstructuremeetthesealing requirement.Meanwhile,themanhole canmeetanti-collapse,stability,fatigueand buckling requirements.Thisstudy indicates thattheellipticalmanholeused in high-pressure fatigueequipmentis feasible.

high-pressure;the ellipticalmanhole;intruding;self-sealing;fatigue;design by analysis

TQ050.3

A

1007-2373(2016)02-0050-05

10.14081/j.cnki.hgdxb.2016.02.009

2015-06-30

河北省自然科学基金（E2011202044）

高炳军（1966-），男（汉族），教授．

数字出版日期：2016-04-26 数字出版网址：http://www.cnki.net/kcms/detail/13.1208.T.20160426.0941.006.htm l