一种改进的变步长LMS算法在Costas环中的应用*
2017-01-04马丛珊娄景艺
马丛珊,高 俊,娄景艺
(海军工程大学 电子工程学院,湖北 武汉 430033)
一种改进的变步长LMS算法在Costas环中的应用*
马丛珊,高 俊,娄景艺
(海军工程大学 电子工程学院,湖北 武汉 430033)
针对传统固定步长LMS算法在稳态误差、收敛速度、跟踪速度方面无法兼得的问题,比较多种不同的变步长LMS算法,提出了一种改进变步长LMS算法。通过对该算法进行仿真分析,发现该算法不仅满足稳态误差、收敛速度、跟踪速度各方面的要求,还减小了噪声对算法的干扰。同时,为了解决科斯塔斯(Costas)环在现实硬件实现中两路信号无法完全一致的问题,将改进变步长LMS算法运用到科斯塔斯(Costas)环中,成功实现了载波恢复。
LMS算法;变步长;科斯塔斯(Costas)环;载波恢复
0 引 言
在短波通信系统接收机中,如何产生与载波信号同频同相的本地载波信号,是最后输出优质解调信号的重要条件之一。而随着通信、导航等行业的发展,对短波接收机的要求也越来越高。而在传统的载波同步方法中,无论是平方环还是科斯塔斯(Costas)环,都需要I、Q两路信号,且要求经过低通滤波器后的两路信号具有频率相同、相位相差90°的特性。然而,现实的硬件设计很难满足。
而在LMS算法中,由于传统固定步长LMS算法[1]无法在稳态误差、收敛速度和跟踪速度方面获得最优性能,因此本文在对多种变步长LMS算法进行讨论的基础上,提出一种改进的变步长LMS算法。仿真分析表明,该算法不仅可满足稳态误差、收敛速度和跟踪速度的要求,而且对噪声有很好的抑制作用。
同时,本文尝试将改进变步长LMS算法运用到科斯塔斯(Costas)环中,只需一路信号,即可完成最后的本地载波提取。
1 算法推导
1.1 固定步长LMS算法
最小均方(Least Mean Square,LMS)算法是线性自适应滤波算法[2]。它包含了滤波和自适应两个基本过程,设计准则是最小均方误差准则(MinimumMean Square Error,MMSE),即滤波器的期望输出与实际输出响应的均方误差最小。设e(n)为滤波器在n时刻的误差,滤波器的输入为x(n),滤波器的输出为y(n),滤波器的抽头权向量为,步长参数为μ。
LMS算法流程如图1所示。

图1 LMS算法流程
(1)输入μ和x(n), x(n)=[x(n),x(n-1),…,x(n-M+1)]T,M为滤波器长度;
(4)计算出滤波器在n时刻的误差e(n)=d(n)-y(n);
(5)计算新的抽头权向量估计值

1.2 变步长LMS算法
为了使LMS算法具有好的稳态误差,同时收敛速度快、跟踪速度快,需要采用改变步长参数的方法[4]。以下就常见的四种变步长LMS算法进行讨论。
(1)基于抽样函数的变步长LMS算法

(2)基于双曲正切函数的变步长LMS算法

(3)基于Lorentzian函数的变步长LMS算 法
在Lorentzian函数y=log[1+e(n)2]的基础上,文献[7]提出了一种新的算法,希望能提高收敛速度和跟踪速度。

(4)基于Sigmoid函数的变步长LMS算法
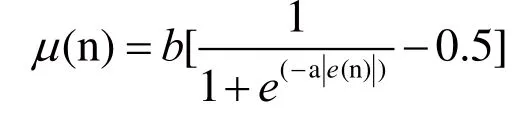
1.3 算法的选择和改进
四种算法的μ(n)和e(n)的关系如图2所示。基于抽样函数的算法在e(n)趋近0时,步长参数μ(n)变化缓慢,但是当e(n)较大时,有很明显的旁瓣。基于双曲正切函数、基于Lorentzian函数和基于Sigmoid函数的算法,在e(n)较大时,μ(n)拥有较快的变化速度,但是在接近稳态时,μ(n)的变化速度没有明显减小,容易造成稳态失调。四种算法里,只有基于抽样函数的算法,在e(n)为0的时候μ(n)可以为0,其余三种算法均存在误差。计算量上,基于Lorentzian函数的算法存在平方项和log项,使得计算量大大增加。同时,四种算法的抗干扰性均不佳。
为了进一步检验四种算法的稳态误差、 收敛速度和跟踪速度,将对这四种算法进行仿真比较。

图2 四种算法的(n)和e(n)的关系对比
搭建仿真平台条件:
(1)滤波器的阶数为2。
(2)迭代次数为2 000。
(3)仿真的统计次数为200。
(4)未知系统的FTR系数为w=[0.6,0.3],在第1 000个抽样点时系统发生突变,突变后的FTR系数为w=[0.5,0.1]。
(5)系统的输入为零均值、方差为1的高斯白噪声。
(6)系统的加性噪声为零均值、方差为0.04的高斯白噪声。
仿真结果如图3所示。

图3 四种变步长算法的比较
如图3所示,在系统稳态误差相差无几的情况下,基于双曲正切函数的变步长LMS算法具有很快的收敛速度和追踪速度。但是,如前文所述,这种算法的抗噪声能力较差。当未知系统存在干扰噪声且噪声的自相关性很强时,算法的性能将受到很大影响。
因此,本文将e(n)改为e(n)e(n-1),从而较好地控制噪声对算法的影响。这是因为误差信号中的噪声自相关性一般很强,而互相关性一般很差,用e(n)e(n-1)可以通过噪声较差的互相关性将其除去,从而降低噪声对步长参数μ(n)的影响[9]。所以,改进后基于双曲正切函数的变步长LMS的相关参数如下:

修改后基于双曲正切函数的变步长LMS算法与原始基于双曲正切函数的变步长LMS算法的仿真比较,如图4所示。修改后基于双曲正切函数的变步长LMS算法在误差信号较大时,拥有较快的收敛速度,而在误差信号接近零时,又拥有较慢的收敛速度,减小了系统的稳态失调。同时,由图5、图6、图7可知,通过改变a、b、h的值,可以改变μ(n)和e(n)的关系。其中,a越大、b越大、h越小时,算法的收敛速度越快。相较b的值,a和h的值更能影响曲线的底部特性。这将影响到e(n)趋近于0时的系统稳定性。此外,算法对a值的变化更加敏感。最终,随着e(n)的增大,步长μ(n)将变为一样。而b值更能影响曲线的初始值。这将影响到系统的最初收敛步长。
此外,通过计算,在输入相同信号和相同噪声的情况下,修改后的算法将原基于双曲正切函数的算法的信噪比提高了10 dB,一定程度上也减小了噪声对算法的影响。
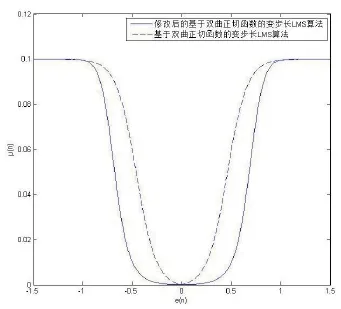
图4 两种基于双曲正切函数的变步长LMS算法的比较

图5 a值变化时μ(n)和e(n)的关系

图6 b值变化时μ(n)和e(n)的关系

图7 h值变化时μ(n)和e(n)的关系
2 科斯塔斯(Costas)环原理
在接收机中,为了获得一个与接收信号载波同频同相的本地震荡信号,需要进行载波同步[10]。载波同步的方法很多,如平方环、科斯塔斯(Costas)环、再调制等。本文采用科斯塔斯(Costas)环进行载波同步。科斯塔斯(Costas)环的载波同步原理 如图8所示。

图8 科斯塔斯(Cos tas)环的原理
接收信号s(t)被送入I、Q两路,分别与va和vb相乘,其中

分别经过相乘器后,可得

经过低通滤波器后,分别可得

将ve与vf同时经过相乘器,有
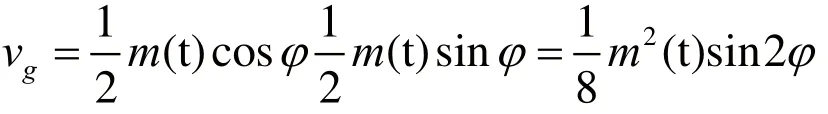
当m(t)为BPSK调制时,m2(t)=1,且当φ很小时,可得

将vg输入到压控振荡器中,调节压控振荡器的输出va。当φ=0时,vg=0,此时的va即为科斯塔斯(Costas)环的输出载波,用它来做相干解调的本地载波时,得到的ve即为解调输出。
3 变步长LMS算法在科斯塔斯(Costas)环中的应用
将改进的基于正切曲线的LMS算法应用于科斯塔斯(Costas)环中,用算法的迭代结果取代原来I、Q两路经过相乘器后的结果,如图9所示。

图9 运用变步长LMS算法的科斯塔斯(Costas)环
接收信号s(t)被送入I路与va相乘,其中

经过相乘器后,可得

分别经过低通滤波器和环路滤波器后,可得

当m(t)为BPSK调制时,m2(t)=1,可得
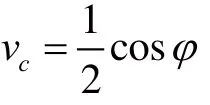
将vc作为LMS算法的输入x(n),而算法的期望输出d(n)=0。通过不断迭代调整,当e(n)→0时,将此时所得的y(n)输入给压控振荡器所得的va,即为运用LMS算法的科斯塔斯环(Costas)环的输出载波,用它来做相干解调的本地载波时,得到的vc即为解调输出。如图10所示,假设信噪比为-20 dB,通过MATLAB仿真,最后φ值趋近于零,此时va=cos(ωct)即为提取的本地载波,符合对科斯塔斯(Costas)环设计的最基本要求。

图10 φ值的变化情况
4 结 语
通过比较前人的算法,提出了一种改进的变步长LMS算法,并将其成功应用于斯塔斯(Costas)环,实现了本地载波的提取。通过仿真分析提出的改进算法变步长LMS算法,发现其不仅满足稳态误差、收敛速度、跟踪速度各方面的要求,还减小了噪声对算法的干扰。同时,通过MATLAB仿真可以看出,这种基于变步长LMS算法的科斯塔斯(Costas)环,可以很好地完成本地载波的提取,很好地解决了科斯塔斯(Costas)环在现实硬件实现中两路信号无法完全一致的问题。
[1] 周志文.变步长LMS算法预失真仿真与实现[J].通信技术,2013,46(09):111-114. ZHOU Zhi-wen.Simulation and Implementation of Polynomial Predistortion Based on Variable-step LMS Algorithm[J]. Communications Technology,2013,46(09):111-114.
[2] Simon Haykin.自适应滤波器原理[M].北京:电子工业出版社,2006. Simon Haykin. Adaptive Filter Theory[M]. Beijing:Publishing House of Electronic Industry,2006.
[3] Kwong R H,Johnston E W.A Variable Step Size LMS Algorithm [J].IEEE Trans on Signal Processing,1992,40(07):1663-1664.
[4] 兰瑞明,唐普英.一种新的变步长LMS自适应算法[J].系统工程与电子技术,2005,27(07):3172-3175. LAN Rui-ming,TANG Pu-ying.New Variable-step LMS Adaptive Algorithm[J].Systems Engineering and Electron ics,2006,27(07):109-112.
[5] 詹国强,吴正国.一种新的变步长LMS自适应滤波算法[J].海军工程大学学报,2006,18(02):109-112. ZHAN Guo-qiang, WU Zheng-guo. A Novel Variable Step Size Adaptive Filtering LMS Algorithm Based on Sample Function[J].Journal Of Naval University Of Engi neering,2006,18(02):109-112.
[6] 张中华,张瑞金.一种新的变步长LMS自适应滤波算法及性能分析[J].系统工程与电子技术,2009,31(09):2238-2241. ZHANG Zhong-hua,ZHANG Rui-jin.New Variable Step Size LMS Adaptive Filtering Algorithm and Its Performance Analysis[J].Systems Engineering and Electr onics,2009,31(09):2238-2241.
[7] 刘剑锋,蒋卓勤,李娟.一种基于Lorentzian函数的变步长LMS自适应滤波算法[J].指挥控制与仿真,2009,31(02):42-44. LIU Jian-feng,JIANG Zhuo-qin, LI Juan. A Novel Variable Step-Size LMS Adaptive Filtering AlgorithmBased on Lorentzian Function [J].Command Control &Simulation,2009,31(02):42-44.
[8] 覃景繁,欧阳景正.一种新的变步长自适应滤波算法[J].数据采集与处理,1997,12(03):171-194. TAN Jing-fan, OU YANG Jing-zheng.New Variable-step LMS Adaptive Algorithm [J].Journal of Data Acquisition & Processing,1997,12(03):171-194.
[9] 沈大伟,贺思.一种改进的变步长变更新速率LMS自适应算法[J].电子测量技术,2007,30(06):52-54. SHEN Da-wei,HE Si.A Modified Variable Step Size and Multi-rate Updated LMS Adaptive Filtering Algorithm and Its Simulation[J].Electronic Measurement Technology,2007,30(06):171-194.
[10] 田嘉,王伟,史平彦.数字Costas环的matlab仿真及其FPGA实现[J].微电子学与计算机,2011,28(11):69-71. TIAN Jia, WANG Wei, SHI Yan-ping. Simulation of Matlab and Implementation of FPGA Platform on Digital Costas Loop[J].Microelectronics & Computer,2011,28(11):69-71.

马丛珊(1990—),女,硕士研究生,主要研究方向为数字理论与技术;
高 俊(1957—),男,博士,博士生导师,教授,主要研究方向为通信理论与技术、无线通信;
娄景艺(1979—),女,博士,副教授,研究方向为数字通信、卫星通信。
Application of A Modified Variable-step LMS Algorithm in the Costas Loop
MA Cong-shan,GAO Jun,LOU Jing-yi
(College of Electronic Engineering, Naval University of Engineering, Wuhan Hubei 430033,China)
Aiming at traditional constant-step LMS algorithm cannot simultaneously satisfy the steadystate error, the convergence speed and tracking speed, comparing different Variable-step LMS algorithm, a Modified Variable-step LMS algorithm is proposed. Simulation and analysis on the algorithm indicate that the algorithm not only can simultaneously satisfy the steady-state error, the convergence speed and tracking speed, but also can decrease the interference of noise. At the same time, it is difficult for Costas to have Identical two-way signal in the hardware implementation. A Modified Variable-step LMS algorithm is applied Costas. It is batter at carrier recovery.
LMS algorithm; Variable-step; Costas loop; carrier recovery
TN911
:A
:1002-0802(2016)-06-0673-06
10.3969/j.issn.1002-0802.2016.06.005
2016-02-15;
:2016-05-07 Received date:2016-02-15;Revised date:2016-05-07
