一种双二元Turbo码盲识别方法*
2017-01-04范雪林
范雪林,王 菊,胥 桓
(中国电子科技集团公司第三十研究所,四川 成都 610041)
一种双二元Turbo码盲识别方法*
范雪林,王 菊,胥 桓
(中国电子科技集团公司第三十研究所,四川 成都 610041)
在智能通信以及电子对抗领域,信道编码盲识别发挥着重要作用。相比于传统Turbo码,双二元Turbo码具有更高的编码效率,因此被广泛使用。针对双二元Turbo码盲识别问题,提出一种编码参数全盲识别方法。该方法对子编码器结构进行深入分析和分解,进而建立分层次识别模型,恢复交织后序列,利用符号匹配方法确定交织关系,完成码字参数全盲识别。通过比对识别参数与预先设定参数,验证该方法具有正确性和有效性。
信道编码;双二元Turbo码;盲识别;交织识别
0 引 言
信道编码由于其特有的纠错能力,可以增加系统提供传输的可靠性以及稳定性,因此在现代通信系统中使用愈加广泛。特别是Turbo码以其接近于香农极限的性能获得了广泛关注。在此基础上,为了获得更高的编码效率、系统性能以及更小的系统延时,人们提出了双二元Turbo码。目前,双二元Turbo码已经应用在多个领域中,如802.16d标准等。
然而,信道编码在给系统性能带来提升的同时,也为自适应通信以及信息处理等带来难度,由此引发了对信道编码盲识别技术的广泛讨论[1-3]。目前,编码盲识别成果主要集中在码长较短的线性分组码、具有循环特性的RS码、1/n和(n-1)/n卷积码以及经典Turbo码的盲识别。在最初的盲识别阶段,文献[4]利用线性分组码的码组内部强约束性,完成了对现行分组码的盲识别;文献[5]利用RS码字的循环特性,采用欧几里得算法,给出了编码参数的盲识别;文献[6]基于中国剩余定理,分解完成参数识别。对于卷积码的盲识别,目前主要有利用欧几里得算法、基于BM的快速合冲算法、基于Walsh-Hadamard变换、基于改进高斯法以及线性矩阵方法等[7-10]。相较于线性分组码及卷积码,人们对Turbo码的识别目前较少,仅由张永光等人通过对编码结构的分析,建立卷积码分析模型,完成了经典Turbo码的盲识别[11-12]。
目前,信道编码盲识别技术已经取得部分成果,但针对双二元Turbo码的盲识别技术成果却是空白。本文的研究成果正好填补这一空白。
1 双二元Turbo码介绍
双二元Turbo码是对经典Turbo码的改进,因此其编码结构与经典Turbo码类似,由两个循环递归系统卷积码编码器构成,寄存器初始状态与末状态一致。图1为802.16d标准所规定的编码器。

图1 双二元Turbo码编码器
每个时刻,同时有两个比特(A,B)输入参与编码。在编码器第一阶段,开关置为1的位置,输入比特(A,B)不仅参与编码,同时作为系统比特直接输出;第二阶段,对输入序列进行交织后,送入子编码器完成编码。此时,只对校验比特输出。一般,对帧长L的数据而言,编码后的总长度为3L。而在实际中,为了实现更高的传输效率,往往会对校验比特进行穿孔而得到更高速率的码字。因此,双二进制Turbo码的识别分析需要识别的未知参数包括码率、子编码器参数、交织参数(交织长度、交织关系、交织起点等)等。
为分析方便,本文以最常见的1/3率双二元Turbo码识别为例,完成对识别算法的分析。
2 双二元子编码器分析
图2为双二元Turbo码的一般子编码器结构。
从图2中可以看出,该编码器类似于1/2率递归系统卷积码(Recursive Systematic Convolutional Code,RSC)编码器,但任意时刻的输入取决于两个比特(视作一个符号)。因此,本文称之为双二元RSC编码器。双二元RSC码的反馈多项式f与前向多项式为y、w如式(1)表示。
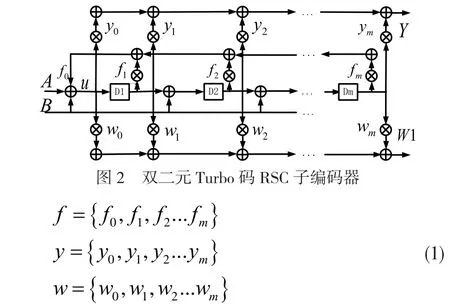
输入数据序列为(A,B),第一个加法器后的数据序列为u。每个时刻同时输入两个比特参与编码,如果第i时刻的输入为(ai,bi),此时有:
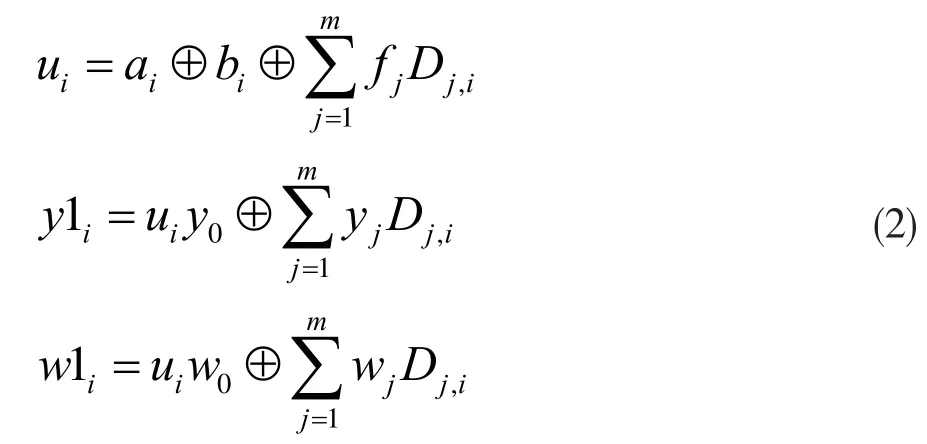
式中,Dj,i表示第j个寄存器在i时刻的状态值,由式(3)获得。

因此,双二进制Turbo码当前时刻的输出不仅与当前输入符号相关,而且与前(m+1)个时刻的输入符号相关,编码约束长度为(m+1)。此外,在任意(m+1)编码约束范围内,码元之间的约束关系完全相同。
将输入及校验序列(以Y1序列为例)按照aibiy1iai+1bi+1y1i+1…(i=0,1,2…)组成新的序列,并做为该编码器的识别数据序列,编码约束长度为3(m+1)。将该序列排列成p×q(p>q,q>3(m+1))的矩阵,当q为3的整数倍时,对该矩阵进行去相关化处理,该矩阵的秩必然小于q,且其左上角单位阵的维数相等。这是由于矩阵每行包含完整的编码约束长度内的码组,且位置对齐时,由于约束长度内的码组约束关系相同,对应矩阵表现为列之间线性相关,因此矩阵秩必然小于q。
定理1 对(n=3,k=2,m)的双二元RSC编码器,编码约束度为m+1,对其识别数据序列所构成的p×q(p>q,q>3(m+1))的矩阵,当q为3的整数倍时,对矩阵进行去相关化处理,矩阵秩小于q,且处理后的矩阵左上角单位阵维数相等。
对双二元RSC识别序列矩阵进行去相关化处理后,左上角单位阵维数反映了约束长度大小。当码字起始位置与矩阵行起始位置重合时,该维数最小。设维数为r(r=3(m+1)-1),则在第r+1列反映了该编码器的约束关系。
定理2 对(n=3,k=2,m)的双二元RSC编码器,编码约束度为m+1,对其识别数据序列所构成的p×q(p>q,q>3(m+1))的矩阵,当q为3的整数倍时,若码字起始位置与矩阵行起点重合,对矩阵进行去相关化处理,处理后的矩阵左上角单位阵维数最小。
通过以上分析,将输入序列及校验输出序列组合,即可完成子编码器参数识别。双二元Turbo未经交织的第一子编码器即满足该识别条件。第二子编码器由于交织器的存在,其编码输入符号序列未知。为完成交织关系识别,需得到交织后数据序列。此时,问题转化为已知子编码器参数及校验输出,求输入符号序列。
设交织后数据序列为(A',B'),编码输出为(Y2,W2)。将图2拆分为如图3、图4所示的两个子结构。


式中,di-t为寄存器状态初始值。根据上式,即可计算得u,B'。
根据图4,则有:

当t-i<0,t-j<0时,ut-i、b't-j值参见式(5)。
由此,根据双二元Turbo码第二支路校验输出,即可得交织后数据序列。
3 双二元Turbo码盲识别
考虑1/3双二元Turbo码,设置编码参数如下:交织长度L、寄存器数m。输入编码序列L长(A,B),第一支路输出L长校验位(Y1,W1),第二支路输出L长校验位(Y2,W2)。输入序列与未经过交织的校验序列满足编码约束关系。第二支路输出的校验位与该约束关系无关,输出块长为6L。因此,对该Turbo码输出序列排列成且q为输出块长的公约数或整数倍时,即每行至少包含一个完整约束长度内的Turbo码。由于在约束范围内,信息位A,B与Y1,W1之间的约束关系相同,表现在矩阵上为列之间线性关系,因此对矩阵进行去相关化处理,矩阵的秩必不等于列数q。
定理3 对1/3率的双二元Tubro码,编码约束度为m+1,对其识别数据序列所构成的的矩阵,当q为输出块长的公约数或整数倍时,对矩阵进行去相关化处理后的秩小于q。
根据定理3,对留存的列值取最大公约数,即可得码长n。去相关处理后,左上角单位阵维数表现了约束长度。因此,当单位阵维数最小时,码字输出块长起始位置与行起始位置重合。由此,即可得输出块长及输出块长的起始位置。
此时,码字的子编码器参数及交织表仍然未知。根据第3小节可知,通过输入序列A,B及第一支路数据Y1,W1,即可完成对子编码器参数的识别。根据已有的子编码器参数,结合Y2,W2序列数据,即可得到第二支路交织后序列然而,通过式(5)可知,这仍然存在一个寄存器初始状态未知的情况。一般来说,由于Turbo译码的复杂度,m一般不超过8。根据式(4),在t<m的时刻,的值由寄存器初始状态决定,由此可得到部分寄存器初始状态值之间的关系。在此关系下,通过遍历得到不同的对于真正的寄存器初态确定原理,可参见文献[3]定理5.3,从而根据交织前后序列包含相同码元的特性完成识别。与文献[3]不同的是,双二元Turbo码为符号之间的交织,若将其交织长度扩展一倍,按照顺序排列,则转化为该文献的识别模型。
至此,对Turbo码的交织关系识别是在已知交织起点、交织长度、交织前后码元的基础上进行的。根据交织并不改变码字汉明重量的特性,结合文献[3],利用多帧数据多次匹配,即可完成交织置换关系识别。与文献[3]不同的是,双二元Turbo码的输入为两个比特(视作一个符号),取值范围为0~3,此时多帧数据任意时刻的汉明重量为符号的汉明重量累加。
4 识别举例
本文以802.16d协议中1/3率双二元Turbo码为例进行识别。设输入序列为(A,B),第一支路输出序列为(Y1,W1),第二支路输出序列为(Y2,W2),交织长度即一帧数据长度为N。将待识别数据序列构成矩阵,结果如图5、图6所示。图5为码长识别结果,图6则为码率识别结果。

图5 码长识别结果
码字长度n为满足条件的q值最小公约数,上图为6。如图5所示,取取n的整数倍,且取尽量大的值)。取该矩阵单位化后对角线上元素,发现除最开始10行外,后面几行呈现出以6为周期的变化,且在一个周期内,1的个数为4,则该码率为4/6。这是由于第二支路为交织后码元编码所得,因此此时呈现码率为4/6。
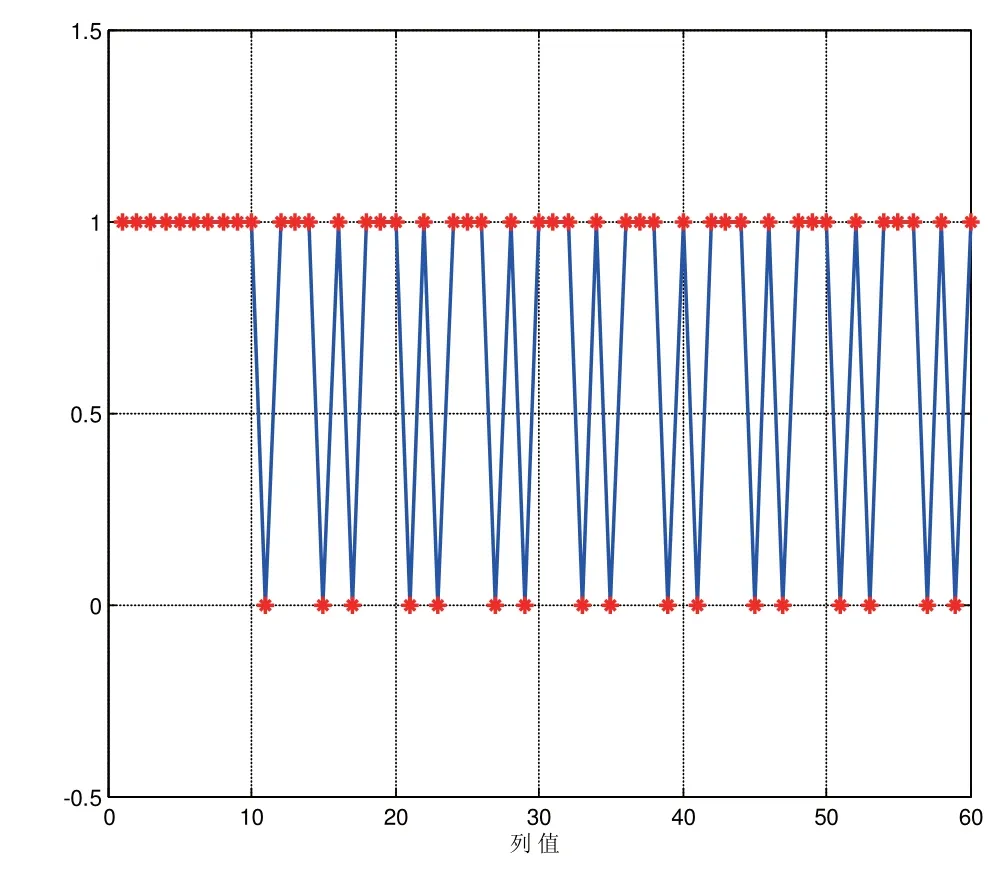
图6 码率识别结果
将输入序列A、B结合校验序列Y1或者W1组成待识别序列,图7、图8为构造的2/3率双二元卷积码识别结果。
由(A、B、Y1)、(A、B、W1)组成的数据序列约束长度为因此有同时,约束关系识别结果为:
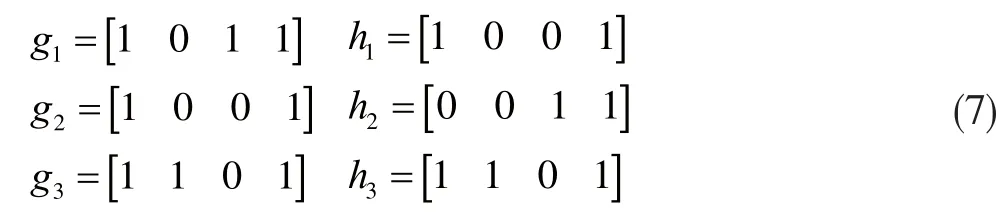
因此,得出反馈多项式、Y1支路多项式,W1支路多项式分别为:

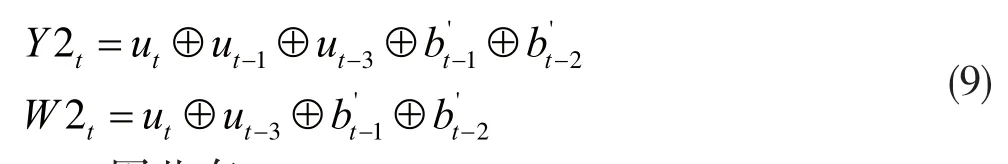
因此有:
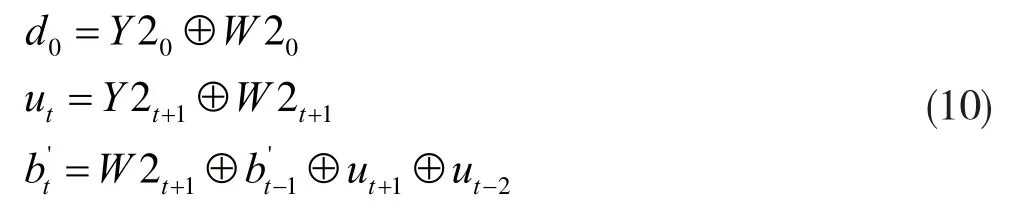
根据式(5)和式(6),有:


图7 (A、B、Y1)序列子编码器参数识别结果
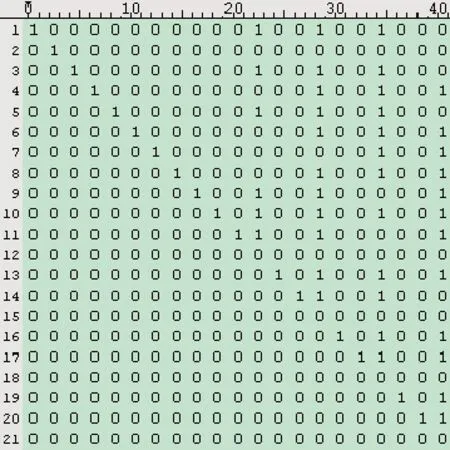
图8 (A、B、W1)序列子编码器参数识别结果
然而,由于寄存器初始状态值d1,d2以及的不确定性,最终将共得到16组值。根据交织前后序列码元完全一致的性质,按照交织前码元+交织后码元的方式组合为新的识别序列,组成p×p(p为 2L的整数倍)矩阵。当为真正的交织后码元时,此时矩阵秩列数达到最小,如图9所示。
从图9中还可得出,码元交织长度为48。对交织置换关系,采用多帧数据多次匹配汉明距离,匹配结果如表1所示。
至此,完成1/3率双二元Turbo码全盲识别分析。
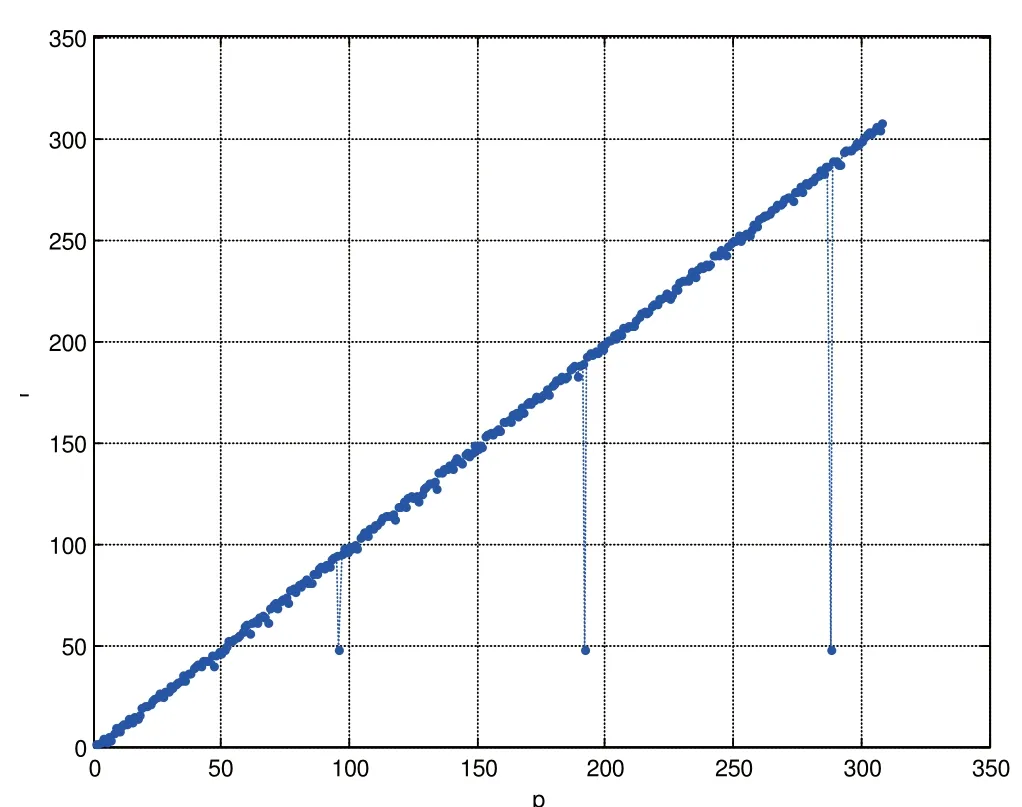
图9 交织长度识别结果

表1 交织关系置换分析
5 结 语
双二元Turbo码有效抑制了传统Turbo码错误平层,但同时也增加了编码器的复杂程度。本文在对双二元Turbo编码器结构深入分析的基础上,对比一般Turbo码结构,分析由B支路引入对整个编码约束关系的影响,完成编码类型及码长识别。同时,为了得到子编码器参数及第二支路交织后编码输入序列,对子编码器结构进行拆解,建立分层次分析模型。最后,基于一种符号匹配方法分析交织关系,完成交织关系识别。此外,综合采用上述方法,以802.16d标准所规定的1/3率双二元Turbo码进行了识别验证,证明该方法具有有效性。
[1] 杨友福,刘建伟,张其善等.卫星信道编码技术及新发展[J].通信技术,2008,41(07):30-33. YANG You-fu,LIU Jian-wei,ZHANG Qis h a n. T e c h n o l o g y a n d D e v e l o p m e n t o f Satellite Channel Coding[J].Communications Technology,2008,41(07):30-33.
[2] Reza Moosavi,Erik G.Larsson. A Fast Scheme for Blind Identification of Channel Codes[C]. Global Telecommunications Conference 2011,Linkoping,Sweden:IEEE Press,2011:1-5.
[3] 张永光,楼才义.信道编码及其识别分析[M].北京:电子工业出版社,2010. ZHANG Yong-guang,LOU Cai-yi. Channel Coding Recognition and Analysis[M]. Beijing:Publishing House of Electrinics Industry,2010.
[4] 陈金杰,杨俊安.一种对现行分组码编码参数的盲识别方法[J].电路与系统学报,2013,18(02):248-254. CHEN Jin-jie,YANG Jun-an.A Method of Blind Recognition to Coding Parameters of Linear Block Cldes[J]. Journal of Circuits and Systems,2013,18(02):248-254.
[5] 戚林,郝士琦,李今山.基于有限域欧几里德算法的RS码识别[J].探测与控制学报,2011,33(02):63-67. QI Lin, HAO Shi-qi,LI Jin-shan. Recognition Method of RS Codes Based on Enclidean Algorithm in Galois field[J]. Journal of Detection&Contr ol,2011,33(02):63-67.
[6] 甘露,周攀.基于中国剩余定理分解的RS码快速盲识别算法[J].电子与信息学报,2012,34(12):2837-2842. GAN Lu,ZHOU Pan.Fast Blind Recognition Method of RS Codes Based on Chinese Remainder Theorem Decomposition[J].Journal of Electronics & Information Technology,2012,34(12):2837-2842.
[7] WANG Feng-hua, HUANG Zhi-tao, ZHOU Yi-yu. A Method for Blind Recognition of Convolution Code Based on Euclidean Algorithm[C]. IEEE International Conference on Wireless Communications,Shanghai:IEEE Press,2007:1414-1417.
[8] 底强,苏彦兵,刘杉坚.基于改进高斯法的卷积码盲识别方法[J].通信技术,2012,45(10):68-74.DI Qiang, SU Yan-bin, LIU Shan-jian. Blind Recognition of Convolution Code based on Improved Gauss Algorithm[J].Communications Technology,2012,45(10):68-74.
[9] 薛国庆,李易,柳卫平.系统卷积码盲识别[J].信息安全与通信保密,2009(02):57-60.XUE Guo-qing,LiI Yi,LIU Wei-ping. Blind Identification of System Convolutional Code[J].Information Security and Communications Privacy,2009(02):57-60.
[10] Johann Barbier,Guillaume Sicot,Sebastion Houcke.Algebraic Approach for the Reconstructtion of Linear and Convolutional Error Correcting Codes[J].International Journal of Applied Mathematics and Computer Science,2006,2(03):113-118.Ali Naseri,Omid Azmoon,Samad Fazeli.Blind Recognition Algorithm of Turbo Codes for Communication Intelligence Systems[J]. International Journal of Computer Science Issues,2011,8(06):68-72.
[11] 张永光.一种Turbo码参数的盲识别方法[J].西安电子科技大学学报,2011,38(04):167-172. ZHANG Yong-guang. Blind Recogniton Method for the Turbo Parameter[J].Journal of Xidian University,2011,38(04):167-172.

范雪林(1985—),女,硕士,工程师,主要研究方向为信道编码盲识别分析;
王 菊(1985—),女,硕士,工程师,主要研究方向为电子对抗、信息安全;
胥 桓(1982—),男,硕士,高级工程师,主要研究方向为网络安全。
A Blind Recognition Method for the Double-binary Turbo Coding Parameter
FAN Xue-lin,WANG Ju ,XU Huan
(No.30 Institute of CETC,Chengdu Sichuan 610041,China)
Blind recognition of channel coding plays an important role in the field of intelligence communication and information countermeasure. Compared to the traditional Turbo code , double-binary Turbo code has higher coding efficiency , so it is widely used.A blind recognition method for the doublebinary turbo coding parameter are proposed for the first time. Based on the analysis of sub-encoder structure and then decomposed it into two parts to establish the hierarchical recognition model. Then recoverying the interleaver sequence of turbo codes by the model, interleaver mapping is dicided by use the symbol matching method. The reliablity of the method are verified by comparing the recognized parameters and pre-set parameters.
Channel Coding; Double-binary Turbo code; Blind recognition; Interleaving recognition
TN97
:A
:1002-0802(2016)-06-0662-06
10.3969/j.issn.1002-0802.2016.06.003
2016-02-03;
:2016-05-05 Received date:2016-02-03;Revised date:2016-05-05
国家自然科学基金(No.61309034)
Foundation Item:National Science Foundation of China(No.61309034)
