洞庭湖入江水道断面调整模式研究

余 蕾，李凌云，卢金友，王加虎,郑 珊

(1.长江科学院 水利部江湖治理与防洪重点实验室，武汉 430010； 2.河海大学 水文水资源学院，南京 210098；3.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072)

洞庭湖入江水道断面调整模式研究

余 蕾1,2，李凌云1，卢金友1，王加虎2,郑 珊3

(1.长江科学院 水利部江湖治理与防洪重点实验室，武汉 430010； 2.河海大学 水文水资源学院，南京 210098；3.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072)

为研究洞庭湖入江水道断面的调整规律，选择城陵矶(七里山)水文断面，根据1962—2010年的实测水沙数据,运用小波分析方法对流量、含沙量序列进行多时间尺度分析，探明了洞庭湖入江水道水沙条件的周期变化规律；并选取城陵矶(七里山)枯水河槽断面面积为特征变量，结合流量小波系数对水沙条件序列进行时段划分；基于滞后响应原理，建立了适用于城陵矶河段断面面积对水沙条件的分时段变化调整模型。结果表明，建立的模型可以较好地模拟洞庭湖入江水道断面的调整规律，计算值与实测值拟合系数R2为0.77。

河床演变；小波分析；多时间尺度；滞后响应；断面面积

1 研究背景

河床演变泛指河流从河源至河口所流经河谷的各个部分的形成和发展的整个历史进程[1]。在有冲有淤的演变过程中，河床会进行自动调整，建立一种与水沙条件或河床边界条件相适应的反馈机制。水沙条件是冲积河流河床形态调整的主要驱动因子，水沙扰动将会促使河床形态发生调整，不平衡输沙是河床演变的实质[2]。

大量研究表明，冲积河流河床演变受当年和前期水沙条件的影响。钱意颖等[3]认为河床形态是水沙多年累积作用的结果，将平滩流量与往年的来水来沙条件联系起来。林秀芝等[4]通过分析渭河下游华县站平滩流量与多年(1～5 a)平均水量滑动值的关系，发现华县站平滩流量Qb与当年来水量Wi的0.7倍和往年来水量Wi-1的0.3倍加权平均水量相关最好，同时发现华县站平滩流量Qb与当年最大3日流量平均值Q3b及往年平滩流量Qi-1的加权组合值(权重分别为0.8,0.2)的相关性较好。Surian等[5]根据大量的实测资料总结出大部分河床再造过程是非线性的指数衰减函数的调整模式，在水沙发生扰动时河床会立刻做出调整，迅速向新的平衡状态靠近，河床再造的速度快。随着时间的推移，其靠近的速度越来越慢。基于这一原理，吴保生[6-7]提出了冲积河流河床演变的调整模式，即

dy/dt=β(ye-y) 。

(1)

式中：y为特征变量；ye为特征变量的相对平衡值；t为时间；β为特征变量的调整速率，可根据实测资料率定。

对式(1)进行积分求解，即

y=(1-e-βt)ye+e-βtye0。

(2)

式中ye0为t=0时刻的平衡值。

在吴保生[6-7]研究的基础上，李凌云[8]根据水沙条件对平滩流量的实际影响情况，调整了初始时刻平滩流量的平衡值Qe0权重，建立了黄河下游平滩流量的滞后响应模型，模拟效果良好。

廖治棋[9]基于李凌云[8]的研究，改进了滞后响应模型的结构和参数，并将其运用到长江中游的荆江河段上，初步揭示了长江流域的滞后响应现象。

总的来看，上述研究考虑了前期一定时期内水沙作用对河床形态的累计影响，建立河床变量与水沙条件之间的响应关系,可以很好地描述河床演变的调整规律。吴保生[6]提出的滞后响应模型对河床演变的内在机理进行了更加全面的阐述，不足之处在于，适用范围局限在我国的多沙河流,并且以往的研究均延续了逐年模拟的特点。但是这种方法对于河道断面较为稳定的河流，逐年模拟存在一定的困难。

河床演变是一个宏观过程，本文拟在吴保生[7]建立的滞后响应模型及李凌云[8]改进的滞后响应模型的基础上运用小波分析方法[10]对洞庭湖汇入长江河道的断面——城陵矶(七里山)水文断面进行水沙的多时间尺度研究，结合长江流域“水多沙少”的特点，基于年平均流量序列的小波系数对水沙条件序列进行时段划分，建立模拟长江流域河道断面面积分时段变化的模型，研究断面面积对水沙条件变化的响应调整规律。

2 城陵矶站水沙的多时间尺度分析

城陵矶(七里山)水文断面位于洞庭湖约8 km 处的出口水道上，下游4 km处是洞庭湖与长江的交汇处，江湖关系十分复杂[11]。

本文拟选取城陵矶(七里山)水文站1962—2010年的流量、含沙量资料，利用小波方法分析城陵矶段水沙的多时间尺度规律。

2.1 小波分析方法

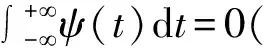
对于给定的Morlet子小波函数，即

ψa,b(t)=e-0.5t2eiw0t。

(3)

式中：w0为常数;i为虚数。

若ψa,b(t)是由式(3)给出的子小波，给定的能量信号f(t)∈L2(R),其连续小波变换为

(4)

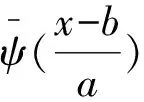
将小波系数的平方值在b域上积分，就可得到小波方差Var(a)，即

(5)

小波分析方法可以呈现水文时间序列的多时间尺度特征，从不同尺度上展现水文序列的波动特性，反映水文过程的变化趋势、预测未来的发展趋势[13]。

2.2 城陵矶站水沙序列分析

将城陵矶(七里山)站1962—2010年的年平均流量、年平均含沙量资料进行标准化处理后,把Morlet小波函数代入式(4)，分别计算出Morlet小波变换系数的实部。正负相位分别用实线和虚线绘制(如图1)，实线代表流量处于丰水期或者含沙量处于偏高期，虚线表示流量处于枯水期或者含沙量处于偏低期。

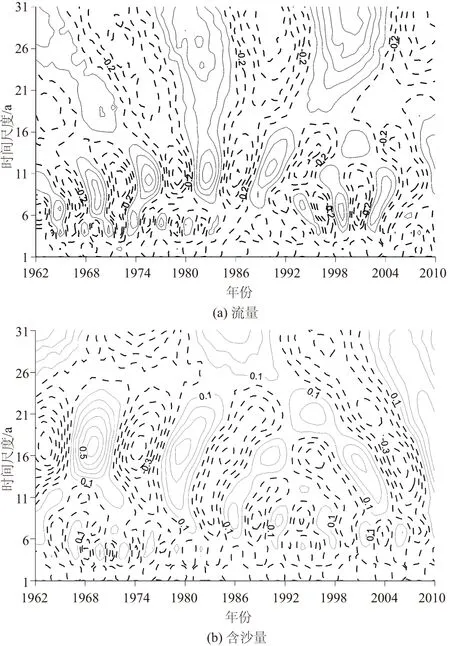
图1 城陵矶站流量和含沙量小波系数实部时频分布Fig.1 Time-frequency distributions of discharge and sediment concentration of Chenglingji station

图1(a)显示，城陵矶站年平均流量存在明显的年代际(>10 a)和年际尺度(<10 a)的周期性变化特征，存在17～30 a,7～17 a及7 a以下3类尺度的周期变化规律，正负相位交替出现。年代际变化中，17～30 a的尺度最为突出，流量经历了丰—平—枯—平—丰—平—枯—平—丰—平—枯 6次循环交替，中心尺度在28 a左右；7～17 a的时间尺度非常突出，流量经历了丰—平—枯—平—丰—平—枯—平—丰—平—枯—平—丰—平—枯—平—丰—平—枯—平—丰—平—枯—平—丰13次循环交替，中心尺度在11 a左右。年际变化中，7 a以下的尺度则出现更多循环。

图1(b)显示，城陵矶站年平均含沙量存在>30 a，14～25 a，8～14 a及6 a以下4类时间尺度。其中，>30 a的时间尺度正负相位虽交替出现，由于受资料限制，中心尺度无法确定；14～25 a时间尺度中，周期性较显著，含沙量经历了低—高—低—高—低—高—低—高8次循环变化，中心尺度在17 a左右；8～14 a时间尺度也较为显著，含沙量经历了高—低—高—低—高—低—高—低—高—低—高—低—高13次循环变化，中心尺度在7 a左右；另外，6 a以下时间尺度则出现更多循环。

由式(5)计算小波方差，并绘制图2，小波方差的波峰可以确定序列的主要变化周期。

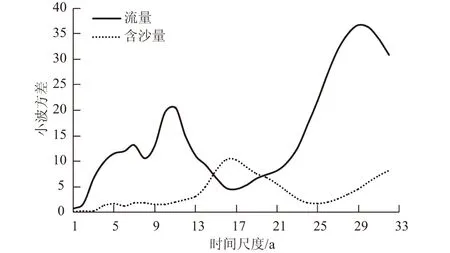
图2 城陵矶站流量和含沙量小波方差Fig.2 Wavelet variances of discharge and sediment concentration of Chenglingji station

年平均流量的小波方差存在3个明显的峰值(图2)，依次为28，11，7 a的时间尺度。其中，28，11 a为主要周期，28 a的周期震荡最强。含沙量的小波方差存在2个明显的峰值(图2)，依次对应着7，17 a，还可判断图中存在>32 a的时间尺度，由于数据有限，有待进一步证实，所以17 a为主要周期。流量、含沙量的主要周期和次要周期共同控制着城陵矶河段水沙的变化特征，而水沙一旦变化，河床形态即会做出响应和调整。

3 城陵矶(七里山)河床断面调整过程的模拟

3.1 特征变量的选取

断面面积[14-15]是衡量河道横断面形态的一个重要物理量，断面面积的变化直接反映了河床的冲刷或淤积，体现了河床的自动调整作用。对于城陵矶(七里山)水文断面，汛期来沙量较大，出流受长江回水顶托的影响大，速度减缓，容易在汛期淤积[16]；非汛期流速较小，造床作用比较稳定，所以选取城陵矶(七里山)枯水河槽(汛后10月份—次年3月份)的断面面积作为本文的特征变量。

从宏观角度来讲，河床演变涉及范围广，历时长，影响因素众多。以往的研究多是逐年模拟河床形态的变化，相比而言，分时段模拟则体现了在某一个时段内水沙的变化比较均匀平缓或者急剧快速的情况下，河床形态的调整过程。

3.2 分时段模型的建立

水沙条件是冲积河流河道形态调整的主要驱动力，长江流域含沙量相对较低，径流量在塑造河床过程中起着决定性作用。因此本文以流量小波系数对水沙条件序列进行大致划分。

根据第3.1节所述，城陵矶站年平均流量小波系数存在28,11,7 a的尺度。第1、第2主周期分别为28,11 a，主要周期决定了流量的变化特征，因此将第1、第2主周期叠加[17]，如图3。

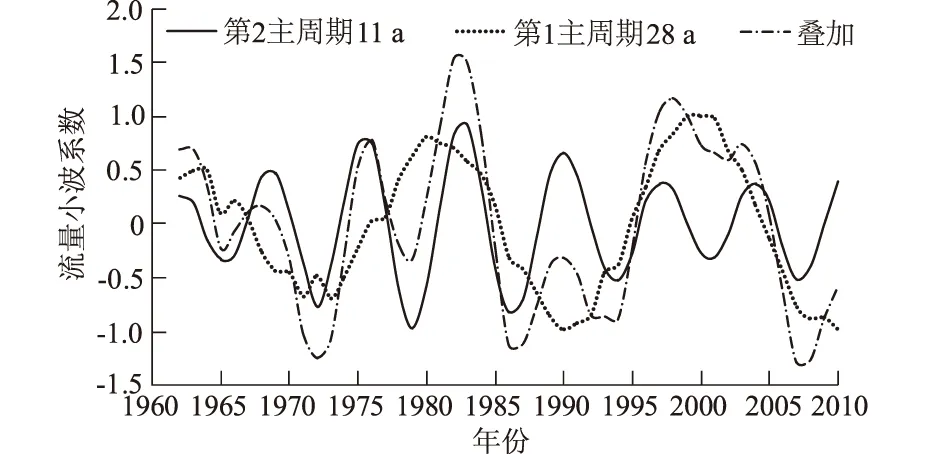
图3 城陵矶站主要周期下流量小波系数Fig.3 Wavelet coefficients of discharge of Chenglingji station under different time scales

根据流量小波系数叠加图，将水沙条件序列依据叠加的小波系数过程线大致分为10段： 1969—1972年、1972—1976年、1976—1979年、1979—1983年、1983—1987年、1987—1990年、1990—1994年、1994—1998年、1998—2003年、2003—2009年。1/4个周期与每一时段的长度大致相当，断面面积随水沙条件发生改变。从叠加的关系中还显示了城陵矶站流量小波系数在未来2～3 a依旧为负值，可以预测年平均流量处于枯水期。

根据对水沙条件序列划分的时段中，每一时段包括n年，n年之中水沙作用是不同的。水沙的“记忆效应”[18]对河道形态的影响较大，根据时段末水沙作用强、时段初作用弱的特点，调整水沙作用权重，其时段初(i=0)水沙权重为1/(1+2+…+n)，时段末(i=n-1)水沙权重为n/(1+2+…+n)，第k时段水沙权重为(k+1)/(1+2+…+n)。并根据长江流域“水多”的特点，引入月均流量最大值Qm。

特征变量平衡值的影响因子是汛期平均流量Qf和汛期来沙系数ξf，与之建立指数函数关系，来沙系数是指单位流量中含沙量的多少[6]。因此，依据上述分段方法和调整的水沙权重，城陵矶河段断面面积平衡值的计算方法如式(6)。

(6)

式中：Aej为第j(j=1,2,…,10)个时段末面积的平衡值(m2)；Qfi为第j个时段中第i年汛期平均流量(m3/s)；ξfi为第j个时段中第i年汛期平均来沙系数(kg·s/m6)；Qmi为第j个时段中第i年月均流量最大值(m3/s);K为系数;a,b,d均为指数，根据实测资料率定。

由此，城陵矶河段的断面面积对水沙的响应调整模式为

Abj=(1-e-βt)Aej+(1-e-βt)e-βtAbj-1。

(7)

式中：Abj为第j时段经过n年水沙累计作用的断面面积(m2)；当j=1时，Ab0为初始年份汛中断面面积(m2)。

在第1时段的水沙作用(n=4)下,断面面积由A0调整至Ab1，除第1时段的初始面积的平衡值由初始年份1969年的汛中面积来确定，余下的每一时段的初始面积平衡值均为上一时段末的断面面积Abj-1。此时，若水沙条件继续发生变化，断面面积Ab1开始调整，经过多个时段(j=1,2,…,10)调整之后，断面面积调整至Abj。

3.3 模型的应用

根据建立的响应调整模型，利用城陵矶河段1969—1985年、1990—2009年实测大断面资料和水沙资料，拟合相应的系数和指数分别为：K=968，a=0.16，b=-0.049 3，β=0.502，d=0.009 8，代入式(6)和式(7)可得适用于城陵矶站的断面面积计算方法为

(8)

Abj=(1-e-0.502t)Aej+(1-e-0.502t)e-0.502tAbj-1。

(9)

对式(8)和式(9)计算值与断面面积实测值进行比较，可得相应的模型计算精度指标。图4给出了小波分析分时段后，利用分时段的模型计算城陵矶站的断面面积，并与实测值进行对比。

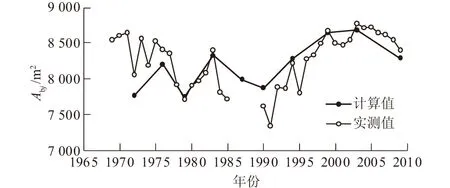
图4 断面面积计算值与实测值时程曲线Fig.4 Time-history curves of section area between calculated and measured values

可以看出，分时段模拟基本能够描述河床形态的调整过程，断面面积在1970—1975年、1990—1996年变化较大。本文所建立的模型较好地模拟了断面面积的总体变化趋势。整体来看，断面面积呈现增—减—增—减—增—减的趋势，河床处于冲—淤—冲—淤—冲—淤的状态。2000年以后，断面面积变化相对比较平稳。

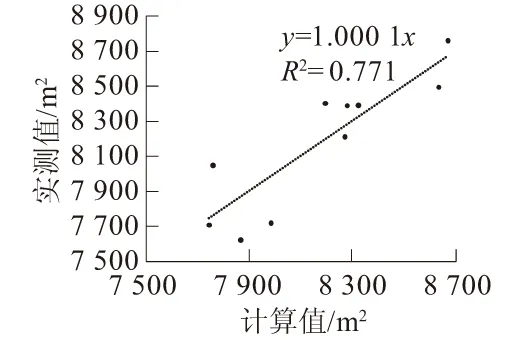
图5 断面面积计算值与实测值拟合曲线Fig.5 Fitted curve of section area between calculated and measured values

图5中，对断面面积计算值与相应的实测值进行了比较。可以看到，当每一时段考虑前期n年内的水沙累计作用(其中n值根据小波分析来确定)，二者拟合系数R2=0.77，计算值与实测值相关关系良好，计算精度较高。

4 结论与展望

(1) 城陵矶河段流量、含沙量具有多时间尺度的特征。城陵矶站的流量序列存在7，11，28 a的变化周期，其中28 a为第一主周期；含沙量序列主要存在7，17 a变化周期，其中17 a为主要周期；主、次要周期共同决定着城陵矶站流量、含沙量的丰枯、高低的多时间尺度规律。水沙条件的改变将会导致河床的自动调整。

(2) 长江流域“水多沙少”，通过水沙的搭配关系、河道本身的特点，建立了断面面积分时段变化的调整模型。本文对分时段模型的基本原理和计算方法进行了阐述，并应用在洞庭湖入江水道断面—城陵矶站(七里山)，计算值与实测值的相关关系拟合系数R2达到0.77，效果较为显著。

(3) 河床演变是一个宏观过程，分时段模拟不失为一种新思路，可以从较大时间尺度上把握冲积河流河床演变的规律。上游来水来沙条件是河床形态调整的主要驱动力，但是本文对于特征变量平衡值Ae的计算只考虑了河段的水沙条件，后续研究可就河床边界条件及人类活动等因素的影响予以考虑，提高模型计算的精度。

[1] 谢鉴衡.河床演变及整治[M].北京:水利水电出版社,1990.

[2] 钱 宁，张 仁，周志德.河床演变学[M].北京:科学出版社, 1989.

[3] 钱意颖，吴 知，米粹侠,等．关于在多沙河流上修建水库保持有效库容的初步分析[C]∥黄河水利委员会.水库泥沙报告汇编.郑州：黄河水利委员会,1972.

[4] 林秀芝, 田 勇, 伊晓燕, 等. 渭河下游平滩流量变化对来水来沙的响应[J].泥沙研究,2005, (5): 1-4.

[5] SURIAN N，RINALDI M.Morphological Response to River Engineering and Management in Alluvial Channels in Italy[J].Geomorphology,2003, 50(4):307-326.

[6] 吴保生.冲河流冲积河流平滩流量的滞后响应模型[J].水利学报, 2008, 39(6):680-687.

[7] 吴保生.冲积河流河床演变的滞后响应模型——I模型建立[J].泥沙研究, 2008,(6):1-7.

[8] 李凌云. 黄河平滩流量的计算方法及应用研究[D].北京:清华大学, 2010.

[9] 廖治棋. 荆江河段平滩面积对水沙条件变化的滞后响应研究[D]. 武汉:长江科学院, 2014.

[10]王文圣，丁 晶，向红莲.小波分析在水文学中的应用研究及展望[J].水科学进展, 2002,13(4):515-520.

[11]卢金友，罗恒凯.长江与洞庭湖关系变化研究[J].人民长江, 1999, 30(4):24-27.

[12]郭文献，夏自强，王鸿翔,等.近50年来长江宜昌站水温变化的多尺度分析[J].水利学报, 2008,39(11):1197-1203.

[13]王文圣，丁 晶，李跃清.水文序列小波分析[M].北京:化学工业出版社, 2005.

[14]李凌云,卢金友,范北林,等.冲积性河流河床横断面形态研究与进展 [J].长江科学院院报, 2014, 31(5):1-6.

[15]章运超,李凌云,范北林,等.长江沙市段断面面积对水沙变异的滞后响应研究 [J].长江科学院院报, 2016, 33(7):1-5.

[16]金升高，陈建湘，彭育元.城陵矶水文站水文断面的代表性分析[J].水利水电快报,1999, 20(18):20-23.

[17]张艳艳，钟德钰，吴保生.黄河平滩流量的多时间尺度现象[J].水科学进展,2012, 23(3):302-309.

[18]梁志勇,杨丽丰,冯 普.黄河下游平滩河槽形态与水沙搭配之关系[J]. 水力发电学报, 2005, 24(6):68-71.

(编辑：占学军)

Model of the Adjustment of Inlet Section fromDongting Lake to Yangtze River

YU Lei1,2，LI Ling-yun1,LU Jin-you1,WANG Jia-hu2,ZHENG Shan3

(1.Key Laboratory of River Regulation and Flood Control of Ministry of Water Resources,Yangtze River Scientific Research Institute, Wuhan 430010, China; 2.College of Hydrology and Water Resources, Hohai University, Nanjing 210098,China; 3.State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072,China )

In order to study the adjustment of discharge and sediment concentration of inlet section from Dongting Lake to Yangtze River, we take Chenglingji hydrological section as an example. According to measured data from 1962 to 2010, we carry out multi-time scale analysis of flow discharge and sediment concentration of Chenglingji station in association with wavelet analysis method to obtain the periodic changes of water-sediment load at the section. Then, we select the section area of low water level as characteristic variables, and use wavelet coefficient of discharge to divide discharge and sediment concentration sequences into different periods. On the basis of delayed response principle, we establish an adjustment model with different time intervals, which is suitable for the response of the water and sediment concentration in the area of the Chenglingji station of Qilishan. Results show that the model could well simulate the regularities of inlet section’s adjustment of Dongting Lake, and the fitted coefficientR2between calculated and measured data is 0.77, which demonstrates that the model has adequate accuracy.

riverbed evolution; wavelet analysis; multi-time scale; delayed response; section area

2015-09-22；

2015-10-23

国家自然科学基金项目(51339001,51209015)；湖北省自然科学基金项目(2014CFB329)

余 蕾(1990-)，女，湖北黄冈人，硕士研究生，主要从事水利工程方面研究，(电话)18061797809(电子信箱)1032602833@qq.com。

10.11988/ckyyb.20150808

2016,33(12):1-5

TV147

A

1001-5485(2016)12-0001-05