滚石的运动速度与冲击力关系的试验研究

韩文奇,余宏明,陈鹏宇

(中国地质大学(武汉) 工程学院，武汉 430074)

滚石的运动速度与冲击力关系的试验研究

韩文奇,余宏明,陈鹏宇

(中国地质大学(武汉) 工程学院，武汉 430074)

研究滚石运动速度与冲击力之间的关系，对于滚石灾害的预防和整治有着重要的意义。滚石冲击力的影响因素众多，其中滚石运动速度的影响较大。通过室内滚石撞击试验，即大理石圆球分别撞击3种不同材料的长方体面板，然后以传感器记录滚石撞击时的冲击力，以摄像机记录滚石运动过程，从而计算得到撞击时滚石的瞬间运动速度，然后观察试验现象并获得相关数据，分析二者的相互作用关系并研究其变化规律，发现滚石运动速度V越大，滚石冲击力F也越大。根据试验结果和数据的拟合，得出两者呈幂函数关系，即F与V的1.35次方成正比例。

滚石; 冲击力; 运动速度；传感器；幂函数关系

1 研究背景

危岩体与母岩彻底分离, 以某种形式向坡下运动时则称为滚石。滚石对其前方的建筑物(拦挡物)会造成很大的危害, 必须采取有效措施进行防治[1-2]。目前对滚石的运动特征研究很多，如黄润秋等[3-6]根据试验研究了坡面对滚石运动时间和对不同形状滚石的运动特征的影响；叶四桥等[7-8]通过分段计算得到落石沿坡面的完整运动路径；唐红梅等[9-10]根据危岩体的不同的破坏模式，推导了落石的运动轨迹方程；何思明等[11-14]对滚石的碰撞恢复系数做了深入的研究，并得到了碰撞恢复系数的计算公式。对于滚石冲击力的研究有日本学者Kawahera等[15]基于落石冲击力试验数据，模拟落石自由下落情形下的落石冲击力；瑞士学者 Labiouse等[16]考虑弹性碰撞理论得到的半经验法公式等。这些研究都是从运动或冲击力1个角度出发研究滚石的特征，所以从试验的角度研究滚石的运动速度与冲击力之间的关系，得出滚石冲击力与运动速度的定量公式，从而利用速度参量简洁地计算滚石撞击物体时的冲击力可能是一个新的尝试，可为泥石流和崩塌的防治提供数据和参数的依据。为了得到滚石运动速度和冲击力的关系，必须获取二者的试验数据。为此，本文通过室内滚石撞击试验，以摄像机记录滚石撞击混凝土板、木板或钢板的运动过程，计算得到撞击时的瞬间运动速度，冲击力则是通过传感器的4个传感通道记录的冲击力数据求和确定。

2 试验装置和材料

滚石撞击试验在成都理工大学地质灾害防治与地质环境保护国家重点实验室(SKLGP)进行，试验选用的仪器设备有传感器、泥石流通道(图1)等；试验的材料选用直径为10 cm的大理石圆球(图2)和30 cm×28.5 cm×5 cm(长×宽×高)的长方形混凝土板、木板和钢板各5块以及400 cm×18 cm×10 cm(长×宽×高)的导向槽、高清摄像机和螺丝刀等。

图1 泥石流通道Fig.1 Model channel of debris flow

图2 大理石圆球Fig.2 Marble ball

3 试验步骤

在所需要的试验材料和仪器准备好之后，具体的试验步骤如下。

(1) 连接传感板上的4个传感通道，接通传感器，然后在传感板上安装1个混凝土板，打开数据记录系统。

(2) 第1个人将1个大理石圆球放在离有刻度的那端1.5 m处，然后松开手，任由它自由滚下。

(3) 第2个人此时打开摄像机并将它对向传感板，保证画面中能看到导向槽中的刻度，记录大理石撞击混凝土板瞬间的运动过程。

(4) 在撞击完后，第3个人操作数据记录系统，存储冲击力的数据。

(5) 再重复同样的试验，取试验数据相差很小的3次有效数据。

(6) 离第1个圆球放置点10～20 cm处，将大理石圆球再次滚下，同时摄像机和数据记录系统再次记录运动过程和冲击力数据。

(7) 再在离第2个圆球放置点10～20 cm处，重复步骤(5)，直至导向槽的另一端。

(8) 然后将混凝土板换成木板和钢板，重复步骤(1)—步骤( 7)。

(9) 进行数据整理分析。

4 试验结果分析

4.1 试验数据处理结果

对滚石撞击试验数据进行整理分析，得到如表1—表 3的结果。

4.1.1 冲击力F的计算

F=FA+FB+FC+FD。

(1)

式中：FA,FB,FC,FD分别为通道A,B,C,D的冲击力数据，计算得F分别见表1—表 3。

4.1.2 滚石运动速度的计算

滚石运动速度是通过摄像机的记录结果进行计算。先将摄像机的录像拷贝到电脑上，然后在电脑上提取帧数，再根据试验前我们在导向槽中标有的刻度，算出运动速度(在电脑上计算每帧通过的距离，1帧是1/25 s；所求的滚石运动速度为撞击物体时的瞬间运动速度，故暂可不考虑滚石材料和坡面材料对运动速度的影响)。算得的结果见表1—表 3。

表1 大理石圆球撞击混凝土板的数据

表2 大理石圆球撞击木板的数据

Table 2 Data of marble ball hitting wood slab

各通道冲击力/NFAFBFCFD力F/N速度V/(m·s-1)474653451910．81554848421930．8310011570403251．1111910089503581．141031041501314881．401181101281304861．421201132521125971．78231142121965901．80

表3 大理石圆球撞击钢板的数据

Table 3 Data of marble ball hitting steel slab

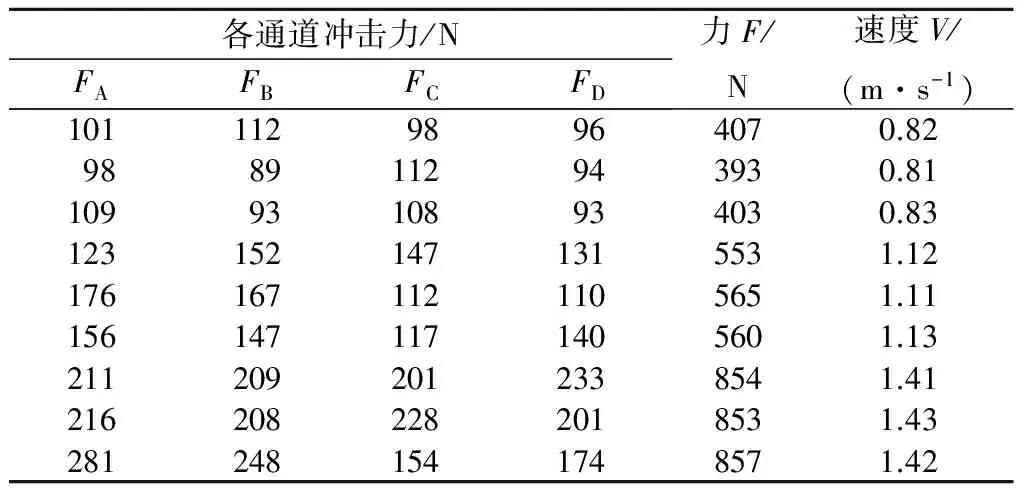
各通道冲击力/NFAFBFCFD力F/N速度V/(m·s-1)10111298964070．829889112943930．8110993108934030．831231521471315531．121761671121105651．111561471171405601．132112092012338541．412162082282018531．432812481541748571．42

4.2 数据分析

4.2.1 滚石运动速度与冲击力关系

对滚石冲击力与滚石的运动速度二者的关系散点图添加趋势线，得出拟合方程和拟合偏差(拟合偏差效果最好的3种)，我们可以看出3种被撞物体对应的拟合方程都存在幂函数关系，所以初步推测滚石运动速度与冲击力呈幂函数关系(见图3)。

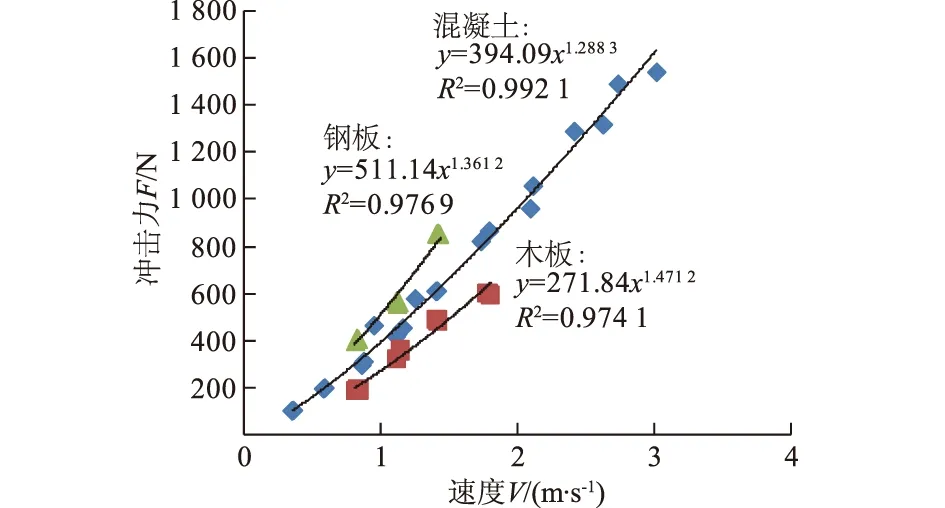
图3 滚石运动速度与冲击力关系Fig.3 Relationship between rockfall velocity and impact force

由图3知，三者的拟合程度最差的拟合系数R2=0.974 1，说明相关性非常好。从图3中可以看出滚石的冲击力大致与运动速度的1.20～1.50次方呈幂函数关系，所以推测滚石冲击力与运动速度的定量公式为

F=CV1.35。

(2)

式中:F为滚石冲击力；C为材料系数,C值与冲积物和被冲击物有关；V为滚石的撞击时的瞬间运动速度。

最后拟合曲线见图4。由图4可知，冲积物为大理石，当被冲击物为混凝土时，C=394.09；当被冲击物为木板时，C=271.84；当被冲击物为钢板时，C=511.14。

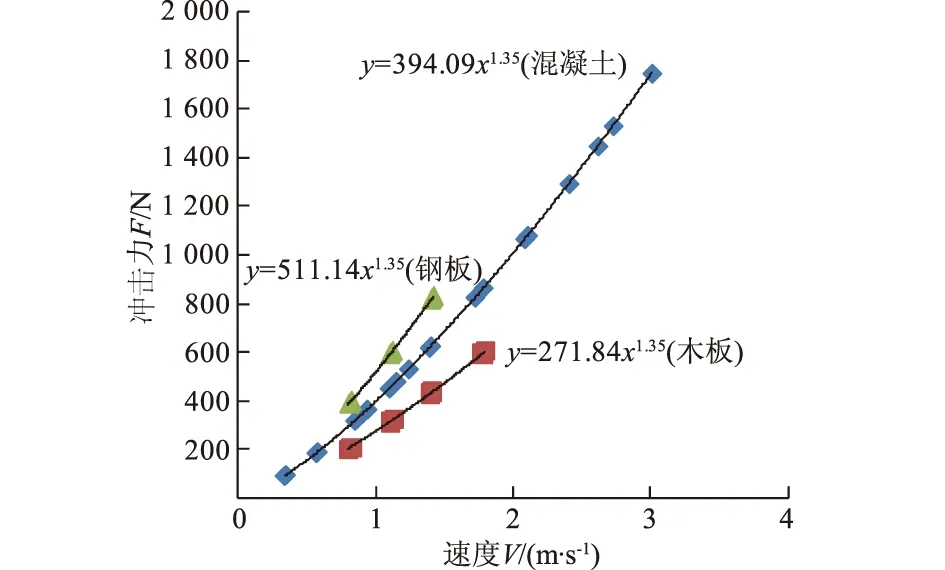
图4 最终拟合曲线Fig.4 Final fitted curves

由图4可知，我们可以看到拟合效果非常好，即滚石的冲击力与运动速度的1.35次方大致成幂函数关系。说明公式是合理的，具有一定的科学性。当给定材料时，测出滚石下落时的瞬间速度和方量，就可以得到滚石的冲击力，即

FL=nLCV1.35。

(3)

4.2.2 与其他试验对此

4.2.2.1 计算公式对比

文献[17]中为了测试冲击力的大小，研制了1套测试冲击力的系统，主要包括滚石运动装置、拦挡装置和数据收集装置3个部分。数据收集部分采用的是传感器和冲击测力仪装置，它可以准确采集到运动过程中的冲击力，显示最大冲击力值，从而最大冲击力计算公式可写为

Fmax=C1[0.25ln(Vsins)+0.720 8]Vsins 。

(4)

式中:s为入射角；C1为材料系数。

本试验的入射角s为90°，故式(4)可化简为

Fmax=C1(0.25lnV+0.720 8)V 。

(5)

本试验得到的公式为F=CV1.35，只需比较(0.25lnV+0.720 8)V和V1.35的之间的关系，在此只是比较一下被撞物体为木板(当被撞物体为混凝土、钢板时，规律相同)时二者的数据，见表4。

表4 其他试验与本试验的数据对比

Table 4 Comparison of data between other tests and the present test

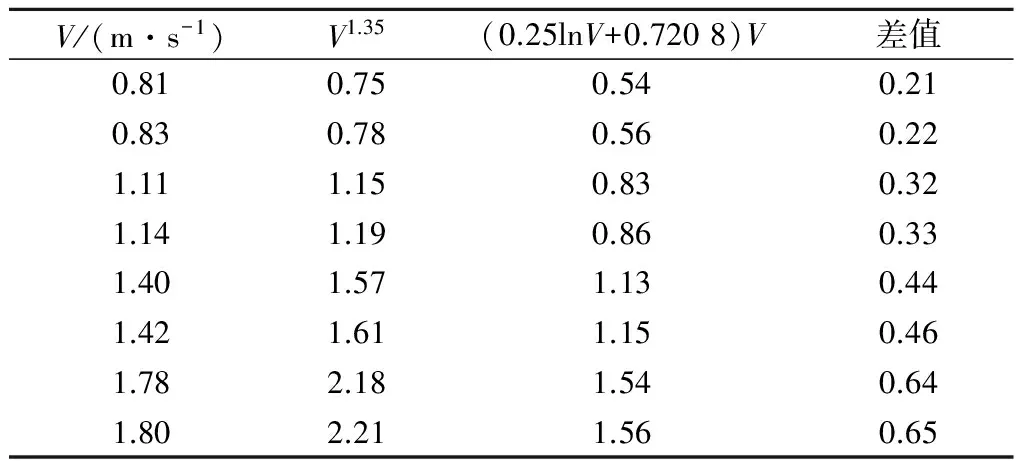
V/(m·s-1)V1．35(0．25lnV+0．7208)V差值0．810．750．540．210．830．780．560．221．111．150．830．321．141．190．860．331．401．571．130．441．421．611．150．461．782．181．540．641．802．211．560．65

注：表中V单位均为m/s。

虽然袁进科等[17]的试验与本试验的数据稍有差值，但是二者的变化趋势是一样的，说明本试验的数据是合理的。

4.2.2.2 试验数据对比

现将袁进科等[17]试验的数据代入本文的公式算得的结果与原文进行对比，见表5，其中V为撞击时的垂向速度。

当速度≥4 m/s时，本文试验(F)与袁进科等[17]的试验(F1)算得的滚石冲击力几乎相等(见图5)。

由图5可知，运动速度越小，二者冲击力差距越大，但总体差距很小，变化趋势也一致，说明本文拟合的公式具有一定的科学性。

表5 其他试验与本试验的冲击力对比

Table 5 Comparison of impact force between other tests and the present test

入射角s/(°)V/(m·s-1)Vsins/(m·s-1)冲击力/N本文文献[17〛6．536．534．965．10905．255．253．704．004．104．102．652．606．535．654．093．75605．254．553．042．824．103．552．181．806．533．262．003．40305．252．621．452．654．102．051．041．80

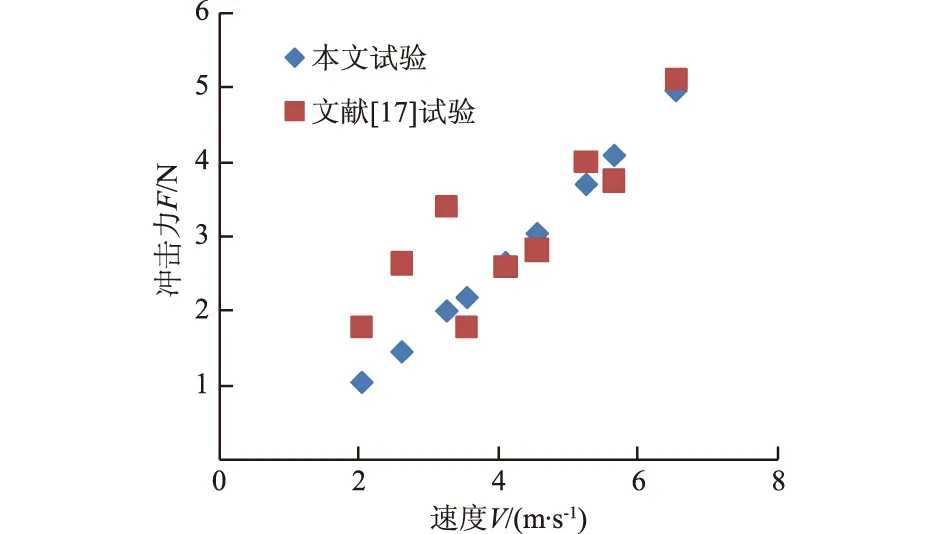
图5 不同试验得出的冲击力与速度的对比关系Fig.5 Relationships between impact force and velocity in different tests

综合上述对比分析，可知试验是合理的，拟合出来的公式具有实际意义。

5 结 论

(1) 不考虑滚石下落到坡脚的运动过程、滚石受到的摩擦力及滚石的类型，单纯地考虑滚石下落到坡脚时的滚石瞬间运动速度和被撞物体材料系数，滚石的冲击力与其垂向的撞击速度呈幂指数关系。

(2) 滚石冲击力与撞击时的运动速度之间的拟合公式为F=CV1.35,冲击物为大理石，当被冲击物为混凝土时，C=394.09；当被冲击物木板时，C=271.84；当被冲击物为钢板时，C=511.14。

(3) 一旦知道滚石的岩性、滚落坡脚的运动速度以及方量，可以运用文中的方法简易得到滚石的冲击力。根据冲击力的大小，我们就可以设置相应的拦挡结构，做出预防和整治。但野外滚石下落到坡脚的运动速度的确定方法值得深入研究，此外，本文试验与其他试验的对比较少，还需进一步搜集相关资料进行对比。

致 谢: 感谢成都理工大学余斌教授、易伟学长对试验的指导和帮助。

[1] 张路青,杨志法,许 兵.滚石与滚石灾害[J]. 工程地质学报,2004,12(3):225-231.

[2] 沈 均,何思明,吴 永.滚石灾害研究现状及发展趋势[J].灾害学,2008,23(4):122-125.

[3] SPADARI M, GIACOMINI A, BUZZI O,etal. In Situ Rockfall Testing in New South Wales, Australia[J]. International Journal of Rock Mechanics and Mining Sciences,2012,49(2): 84-93.

[4] JONES N, ALVES M. Post-severance Analysis of Impulsively Loaded Beams [J].International Journal of Solids and Structures ,2004,41(22/23):6441-6463.

[5] 黄润秋,刘卫华,周江平,等.滚石运动特征试验研究[J].岩土工程学报,2007,29(9):1296-1302.

[6] 黄 雨,孙启登,许 强.滚石运动特性研究新进展[J].振动与冲击,2010,29(10):31-35.

[7] 叶四桥,陈洪凯,许 江. 落石运动模式与运动特征现场试验研究[J].土木建筑与环境工程,2011,33(2):18-23,44.

[8] 叶四桥，唐红梅，祝 辉．基于落石运动特性分析的拦石网设计理念[J]．岩土工程学报，2007，29(4):566- 571．

[9] 吕 庆,孙红月,翟三扣,等. 边坡滚石运动的计算模型[J]. 自然灾害学报,2003,12(2):79-84.

[10]唐红梅,易朋莹.危岩落石运动特征研究[J].重庆建筑大学学报, 2003,25(1):17-23.

[11]何思明,吴 永,杨雪莲. 滚石坡面冲击回弹规律研究[J].岩石力学与工程学报,2008,27(增1):2793-2798.

[12]章广成,向 欣,唐辉明. 落石碰撞恢复系数的现场试验与数值计算[J].岩石力学与工程学报,2011,30(6):1266-1273.

[13]柳 宇. 滚石坡面运动恢复系数研究[D].成都:成都理工大学,2012.

[14]CHAU K T, WONG R H C，WU J J ,etal. Coefcient of Restitution and Rotational Motions of Rockfall Impacts[J].International Journal of Rock Mechanics & Mining Sciences, 2002,39(1): 69-77.

[15]KAWAHARA S, MURO T. Effects of Dry Density and Thickness of Sandy Soil on Impact Response due to Rockfall[J]. Journal of Terramechanics, 2006, 43(3): 329-340.

[16]LABIOUSE V, DESCOEUDRES F，MONTANI S. Experimental Study of Rock Sheds Impacted by Rock Blocks[J]. Structural Engineering International Journal, 1996, 3(1): 171-175.

[17]袁进科,黄润秋,裴向军.滚石冲击力测试研究[J].岩土力学,2004,35(1):49-53.

(编辑：占学军)

Experimental Study on Relation between Rockfall Velocityand Impact force

HAN Wen-qi, YU Hong-ming, CHEN Peng-yu

(Faculty of Engineering, China University of Geosciences, Wuhan 430074, China )

Researching the relationship between rockfall’s impact force and rockfall velocity is of great significance for the prevention and remediation of rockfall hazard. The impact force of rockfall involves many factors, among which velocity is the most influential factor. In this article, the relationship between rockfall velocity and impact force was researched through indoor impact test. First, marble ball was released to hit rectangular slabs made of different materials. Second, the rockfall’s impact force was recorded through sensors and rockfall movement by using camera. Third, the instantaneous velocity at the moment of hitting was calculated, and some related data were obtained. Results reveal that the large rockfall movement velocity (V), the greater the impact force (F) of rockfall. According to the results and the fitted data, the velocity and impact force are in a power function relationship, i.e.Fis positively related withV1.35.

rockfall; impact force; velocity; sensor; power function relationship

2015-06-12；

2015-07-30

国家自然科学基金项目(41272377)

韩文奇(1989-)，男，安徽潜山人, 硕士研究生，研究方向为地质灾害防治与风险评估,(电话) 13258357986 (电子信箱) 892396819@qq.com。

10.11988/ckyyb.20150492

2016,33(12):42-45，50

TU452

A

1001-5485(2016)12-0042-04