基于图论算法的高校排课系统分析

2017-01-03杜衡吉

西部皮革 2016年22期

关键词：图论权值教室

杜衡吉

(曲靖师范学院信息工程学院，云南曲靖 655011)

基于图论算法的高校排课系统分析

杜衡吉

(曲靖师范学院信息工程学院，云南曲靖 655011)

高校学生人数以及课程设置众多，排课工作十分繁重。随着时代的发展，各种教育信息化的应用逐渐规模化，高校校务系统、办公自动化系统以及网上排课系统等也得到快速的发展。在进行排课系统设计的时候，可以采用不同的算法。本文以图论算法为例，分析相应的高校排课系统设计方法。

图论算法；高校；排课系统

1 前言

高校的教育教学工作中，排课是一个必不可少的重要环节。从本质角度进行分析，排课的实质在于对学校所设置的各种课程进行合理的安排，进行一组适当的教学时间与空间安排，以保证整个教学活动可以按照一定的秩序和计划顺利开展。但是，在实际的排课过程中，存在十分复杂的情况，需要对课程分布情况和时间分配情况以及教师、教室等情况予以综合性的考虑和安排，受到多方面条件的约束。

2 排课问题的图论算法

在对排课问题进行研究的时候，可以选择使用不同的算法，包括遗传算法和退火算法以及图论算法等。其中，遗传算法和退火算法存在一定的应用局限性。而图论算法则可以对一定的问题进行转化，将其转化为图论问题。之后，利用图论的基本算法进行解决，达到解决实际问题的目的。在排课过程中，受到高校日常教学情况的影响，相应的不同元素存在太多的组合可能性，十分复杂。此时，可尝试利用图论算法进行解决。首先，对模型进行合理的简化，将其简化为两个子模型，之后，对上述两个优化过程进行转化，将其转化为图论问题予以解决。按照图论算法相关定理，对模型予以初步优化。之后，以图论的完美对集理论为基础，结合教学效果对排课模型图中的一些边赋了权值，选出权值最大加权图，最终得出最优的排课方案。

3 基于图论算法的高校排课系统分析

3.1 初始模型的建立。采用图论算法解决排课问题的第一步是将其先转化为二分图边染色问题。现在假设一共有5个班级，需要由 4 位老师进行授课。对于班级和教师之间的对应关系，可以利用图1的二分图予以表示。在实际的教学过程中，同一时间内，一名教师只能给其中的一个班级授课，而同一时间内一个班级不能由两名老师授课，则可以获得图2 的着色方案。

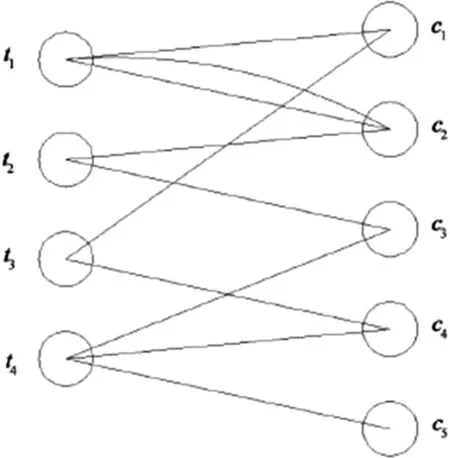
图1 排课图

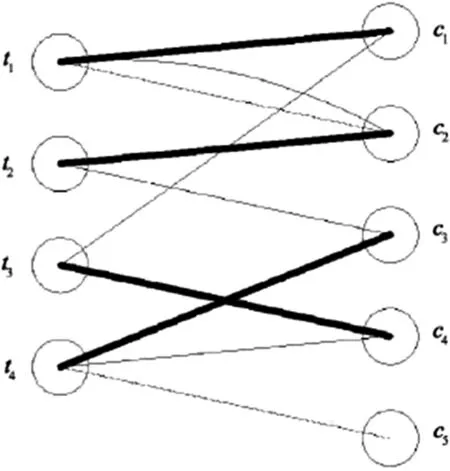
图2 染色后的排课图

3.2 排课模型的优化。按照上文的分析，在进行排课的时候，如果单纯使用边着色理论，只能确保从时间角度教师与班级不发生冲突。无法保证可以满足教学方面的需求。另外，在进行排课的时候还要考虑到一些特殊情况。这样一开，便需要对排课的效果进行优化设计。构建的权值函数如下：

ω(tici)=ω1(tici)+ω2(tici)+……+ωn(tici)

在具体模型分析的时候，可以结合实际情况，通过权值函数对图中的每条边都进行相应的赋值。最终的最优排课安排计划，即为所有加权图中权值最大的图。

3.3 排课管理系统的设计。为了更好的解决高校排课表问题，设计开发一个简易排课管理系统。通过该系统，可以生成一定的排课安排，很好的满足日常教学的需求。整个系统包含多个不同的功能模块，通过不同的模块，可以实现排课管理和课表查询等，排课管理系统功能模块设计示意图如图 3所示。

图3 排课管理系统功能模块设计示意图

在系统中进行数据交换的时候，底层数据库为Excel。在进行排课之前，首先对涉及到的班级和教师进行汇总，输入Excel中，之后，使用一定的函数，对MATLAB与Excel进行数据交换。并利用一定的函数对边着色问题予以解决，实现对课时的合理安排。

3.4 排课系统的应用效果。手工排课一向是学校教务工作中最令人头疼的事，非常费时费神，而且由于人工操作时多多少少会有些失误。而通过对设计的排课系统予以实际应用，网上选课及计算机排课子系统将按行政班教学和按选课形成的教学班教学两种模式融合，自然过渡，面向教学管理链实行教学资源的动态管理，以排课为中心，将教学任务安排、排课、选课、考试安排、教室调配、任课教师管理、学籍管理等统一在一个管理链上，在教学资源管理调配和统计分析等方面充分融合。系统还可以提供自动和交互两种排课方式，提供两类学生上课视图、教师上课视图和教室使用视图，课程安排情况一目了然，操作直观、简单、便捷。教室调配子系统与排课系统联动，进行借用管理、查询和分析统计，生成全校教室使用情况汇总表。考试安排子系统根据学生选课结果安排考试时间和教室，保证每名学生考试时间不冲突。经过一段时间的应用，获得了理想的应用效果，排课效果良好，课程安排秩序井然。