一种基于大气层外解析动力学模型的最优迭代制导方法

郑旭, 高长生, 陈尔康, 荆武兴

(哈尔滨工业大学 航天工程系, 黑龙江 哈尔滨 150001)

一种基于大气层外解析动力学模型的最优迭代制导方法

郑旭, 高长生, 陈尔康, 荆武兴

(哈尔滨工业大学 航天工程系, 黑龙江 哈尔滨 150001)

固体火箭在实际飞行过程中其发动机参数会产生较大的摄动偏差,而传统的摄动制导很难保证较高的制导精度,甚至会发散。另外,采用动力学数值积分的显式制导算法进行实时计算又会带来较大的计算量,从而难以满足实际飞行的要求。针对这一问题,提出了一种基于大气层外解析动力学模型的最优迭代制导方法。首先在大气层外推导了解析动力学模型,然后基于Pontryagin极大值原理推导了最省燃料的推力控制方法,以共轭状态向量和飞行时间为迭代变量给出了带有多种终端约束的迭代制导算法。仿真分析了发动机参数和火箭初始状态在最大正偏差以及最大负偏差情况下迭代制导精度,并进行了蒙特卡罗打靶仿真。仿真结果表明,提出的基于大气层外解析动力学模型的迭代制导算法计算时间少、制导精度高、鲁棒性强,具有较好的工程应用价值。

固体火箭；迭代制导方法；解析解；极大值原理；蒙特卡罗打靶

固体火箭推进技术以其结构简单、维护简便、比冲高、反应快速、成本低等[1]优点在各类火箭、导弹武器中得到了广泛应用。世界各军事大国投入了大量经费对固体火箭进行了研究,据统计,固体火箭在弹道式火箭中的比例达到了90%以上。虽然固体火箭较液体火箭具有诸多优点,但是其自身存在的缺陷也不容忽视,如固体火箭具有易燃易爆、对药柱浇铸质量严格、容易造成燃烧不稳定等缺点。其中固体火箭发动机在实际工作中的燃烧不稳定会造成发动机较大的推力偏差和比冲偏差[2],而这对火箭要实现高精度制导提出了很高的要求。

为了消除干扰以保证较高的交班点精度,传统的运载器大多采用摄动制导策略。采用摄动制导的运载器射前参数装订到弹载计算机,计算量小,但摄动制导存在致命缺陷,如火箭发射前要进行大量的计算工作,而且其理论依据是基于小扰动的假设,因此像固体火箭发动机这样在大参数摄动情况下其制导精度会显著降低。针对固体火箭在飞行过程中面临参数大扰动的问题,迭代制导方法得到了广泛应用研究。迭代制导不需要在火箭发射前进行大量计算,其优势是利用弹载计算机进行实时制导计算,其主要特点是运载器(火箭、弹道导弹、航天飞机等)在标称弹道附近存在多条飞行轨迹,是一种路线自适应制导方法,具有很高的制导精度[3]。

目前,在迭代制导计算中动力学模型大多采用数值计算方法,需要消耗大量时间,难以满足实时计算的要求。文献[4-5]将状态方程和代价函数分别进行线性近似和二次近似,提出了一种新的迭代算法来解决满足多重约束条件下的最优控制问题。文献[6-7]通过数值方法研究了运载器上升段闭环迭代制导方法,得出了满足多种过程和终端约束条件下最优轨迹。文献[8]在线性化的引力场中提出了一种迭代算法用于解决脉冲燃料最优交会问题,给出了详细的迭代算法流程。文献[9-10]在研究共面有限推力轨道转移和运载器上升段大参数摄动问题时,基于极大值原理推导了最省燃料的控制模型,给出了两点边值问题的迭代算法。文献[11-12]从最优控制出发,以推力的3个分量为控制变量,推导出了液体运载火箭的一种迭代制导算法,并分析了火箭发动机参数偏差对入轨点精度的影响。文献[13]推导了运载火箭大气层外满足大姿态机动的自适应制导方法,仿真得出了最优飞行轨迹。

虽然迭代制导方法具有较高的制导精度,但动力学模型中采用数值计算方法将会消耗大量时间,导致工程适用性不强。当固体火箭穿过稠密的大气层后,由于气动力影响很小,因此可以简化动力学模型,给出具有解析动力学模型迭代制导算法,进而减少弹上计算时间。本文首先在发射惯性系中推导固体火箭大气层外动力学模型的解析解,然后基于极大值原理给出以最省燃料为性能指标的迭代制导算法,以共轭状态向量和飞行时间为迭代变量求解满足关机点状态约束的最优姿态角,最后对固体火箭发动机参数存在大偏差情况下进行仿真分析,验证该迭代制导算法的有效性、实用性和鲁棒性。

1 大气层外飞行动力学模型的解析解

固体火箭二级飞行时已在大气层外,此时可忽略气动力的影响。假设发动机的推力沿着弹体轴方向,则火箭在发射惯性下的动力学模型为

(1)

式中,r为火箭相对发射惯性系下的位置矢量,v为火箭相对发射惯性系下的速度矢量,g(r)为引力加速度矢量,aP为推力加速度向量。

由于g(r)是位置的函数,为求得动力学模型的解析解,取g(r)为飞行时间内的平均值,即

(2)

式中:g(r0)为初始位置r0时的引力加速度;g(rk)为关机点位置rk时的引力加速度。

首先令g(r)=g(r0),代入动力学模型的解析解(13)、(18)式得到关机点状态参数,然后通过关机点位置rk求得g(rk),于是得到了(2)式中的g(r),然后再代入后面的动力学模型解析解得到rk,进而求得g(rk)和g(r)。重复以上过程,直到g(r)变化不大。

推力加速度aP可表示为

(3)

推力方向u可以表示成姿态角的函数,即

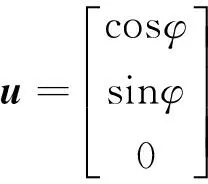
(4)

式中，φ为火箭相对于发射惯性系下的俯仰角。这里保持偏航角ψ和滚转角γ为零。

在进行弹道设计时,设定俯仰角飞行程序为

(5)

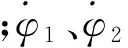
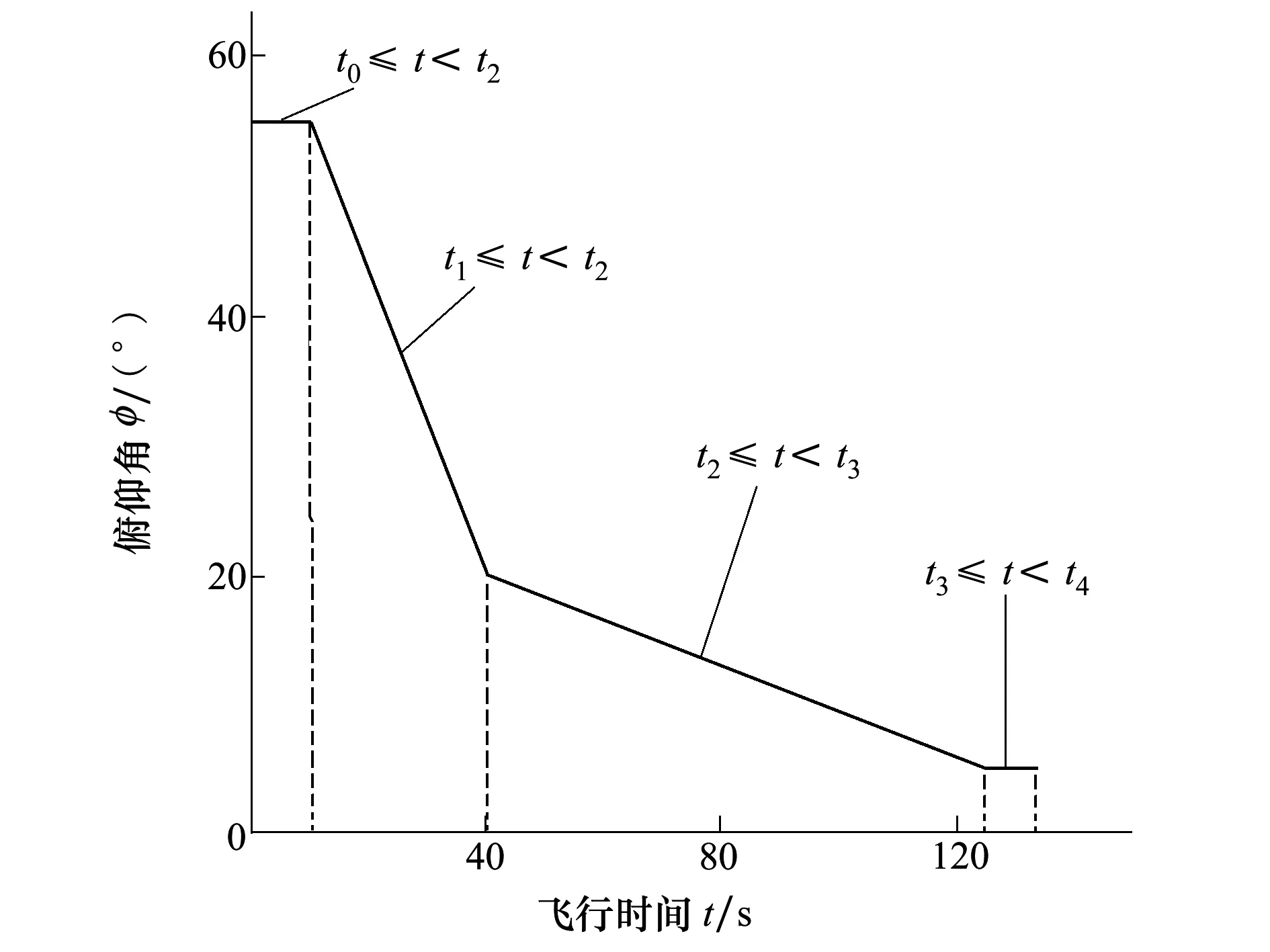
图1 设计的俯仰角变化值

将(4)、(5)式代入(3)式中,得到推力加速度为[17]

(6)

式中

于是动力学模型(1)可以改写成

(12)

(13)

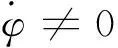
(14)

其渐进表达式为

(15)

式中

(16)

令

(17)

于是,积分微分方程(12)可得解析解为

(18)

于是,我们就得到了发射惯性系下大气层外飞行动力学模型的解析解,即公式(13)、(18)。

2 最省燃料的控制模型

为了得到最省燃料的控制模型,需要将动力学模型与最优控制相结合,求解最优姿态角φopt。

动力学模型(1)中g(r)可以简化为

g(r)=-ω2r

(19)

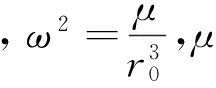
动力学模型(1)可以改写成

(20)

最省燃料的控制模型可以描述成:根据火箭当前的状态r(t)和v(t),选取最优的控制变量u(t),满足关机点的约束状态r(tk)和v(tk),且使火箭以最短的时间到达关机点,即使指标

(21)

达到极大。这里我们可以看出,此性能指标极大与时间最短达到关机点等价。

达到极大。这里我们可以看出,此性能指标极大与时间最短达到关机点等价。

选取哈密顿函数为

(22)

式中,λr、λv分别为r、v的共轭状态。

由Pontryagin极大值原理,最优的推力方向u应使哈密顿函数H达到极大,由此我们可以得出

(23)

可见,最优的推力方向为共轭状态λv的单位向量。

于是由(4)式可以得出最优φopt的表达式为

(24)

动力学模型(20)的共轭状态方程满足

(25)

具体展开为

(26)

由此得到共轭状态向量λr和λv的解析表达式为

(27)

式中,λv0、λr0为共轭状态向量初始值。

3 边界条件

3.1 终端约束条件

由于火箭在每个制导周期内进行迭代制导过程中必须保证火箭关机点状态满足相应的约束条件,这里给出关机点处的约束误差表达式。

横向误差

(28)

式中,rz为位置向量r的z方向分量,rzk为标称关机点z方向位置分量。

高度误差

(29)

式中,re为火箭实际关机点地心矢径,为re=r+R0,rke为火箭标称关机点地心矢径,rke=rk+R0。R0为发射点地心矢径,rk为标称关机点位置向量。

射程误差

(30)

式中,Re为地球平均半径,为6 378.140 km。

速度倾角误差

(31)

式中,rk、vk为标称关机点的位置和速度矢量。

横向速度误差

(32)

式中,vz为速度向量v的z方向分量,vzk为标称关机点z方向的速度分量。

速度误差

(33)

由(28)～(33)式得到终端约束的向量为

(34)

3.2 横截条件

由前面所得到的终端约束向量g,可得出满足共轭状态的横截条件为

(35)

式中,k∈R6×1,为拉格朗日乘子向量,tk为助推段飞行时间。

哈密顿函数在最优轨迹终点处的取值满足

(36)

4 迭代变量和迭代制导算法

4.1 迭代变量

由前面的论述可以看出,火箭的俯仰角φ与发动机的推力矢量方向u密切相关,而u又是共轭向量λv的单位向量。

因此,可以选择迭代变量λv0、λr0和tk来规划火箭的飞行轨迹。通过λv0和λr0可以解析得到λv和λr,进而可以得出火箭在剩余飞行时间段内的推力方向u,再根据当前的状态和剩余飞行时间可以通过动力学模型解析解,得到关机点处的状态rk和vk,这里只有满足终端约束向量g和横截条件(35)、(36)的λv0、λr0和tk才是符合要求的。因此,通过多次迭代得到在每个制导周期内的最优飞行轨迹,直至满足终端约束条件时关机,迭代制导流程如图2所示。

图2 迭代制导流程图

4.2 迭代制导算法

根据以上分析,将满足终端约束向量g和H(tk)记为终端约束条件G,即

(37)

取迭代变量为

(38)

在飞行过程中某个制导周期内,假设存在ξ*,通过(23)式、(24)式、(27)式得到火箭最优姿态角,然后利用动力学模型的解析解求解关机点状态量。ξ*需满足G(ξ*)=0,设经过j步迭代得到ξj,在ξj附近进行一阶泰勒展开,则

(39)

于是得到

(40)

迭代终止条件为

(41)

式中,ε为给定的精度值。当在某个制导周期内满足终止条件时,迭代停止,火箭按照当前的姿态角飞行至关机点。

5 仿真计算

发射点为东经117.3°,北纬39.9°,目标点西经74°,北纬40.7°,发射方位角为31.4°。火箭相关参数为:推力为750 000 N,比冲为3 000 m/s,燃料质量为55 000 kg,有效载荷为1 000 kg,总质量为63 000 kg。火箭在给定的初始状态下按照设计的姿态角程序飞行至关机点,得到了关机点状态参数。火箭的初始状态和终端状态参数如表1所示。

表1 初始状态和终端状态参数

5.1 最大偏差条件下的仿真分析

固体火箭相关误差参数的最大偏差值如表2所示,制导周期T=10 s。另外,仿真设定固体火箭初始位置偏差为Δr0=[700 600 500]Tm,初始速度偏差为Δv0=[8 7 5]Tm/s。 在两种最大偏差条件下,仿真得到结果如表3、图3和图4所示。

表2 误差参数的标称值、最大正偏差(Case1)

表3 Case1和Case2情形下迭代变量计算值

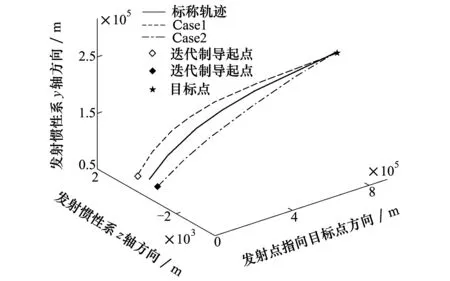
图3 Case1、Case2情形下迭代制导轨迹

图4 Case1、Case2情形下姿态角变化

仿真采用的计算机配置为:Intel(R) Core(TM) i3-2100 3.10GHz 的CPU,内存3GB。当采用数值迭代算法在一个制导周期内得到制导指令所用时间为8.56 s,而本文采用的解析模型迭代制导算法所用时间仅为0.18 s,提高了几十倍的计算效率,可以满足实时计算的要求。

表3为固体火箭在2种大参数偏差情况下迭代变量优化值，图3、图4为迭代制导得出的三维飞行轨迹和姿态角变化，可以得出，火箭在2种大参数偏差条件下的制导轨迹满足标称关机点状态约束条件，制导精度高、鲁棒性强。

5.2 蒙特卡洛打靶仿真

假设各偏差均服从正态分布,仿真加入的3σ偏差值如表4所示。进行1 000次打靶仿真,得到的误差参数如图5～图7所示。

表4 各误差参数3σ值

从图5～图7看出,在给定误差参数条件下,固体火箭关机点高度误差最大为0.1 m,关机点横向误差最大为0.001 m,关机点射程偏差最大为0.25 m,落点纵向偏差最大为25 m,落点横向偏差最大为4 m。另外,各偏差参数均集中在零附近。仿真表明本文提出的大气层外基于解析动力学模型的迭代制导算法不仅计算效率高、实时性强,而且还可以保证较高的制导精度和较强地鲁棒性。

图5 关机点横向、高度误差 图6 关机点射程误差 图7 落点纵向、横向偏差

6 结 论

本文针对固体火箭飞行过程中存在大偏差以及显式制导计算耗时的问题,结合最优控制提出了一种基于大气层外解析动力学模型的最省燃料迭代制导方法,以共轭状态向量和飞行时间为迭代变量求解了满足多种关机点状态约束的最优姿态角。最后仿真分析了固体火箭发动机参数和初始状态参数存在最大正负偏差情况下的迭代制导精度,并进行了蒙特卡洛打靶仿真。仿真结果表明所提出的迭代制导方法计算时间少、精度高、鲁棒性强,具有较好地工程实用价值。

[1] 寇军强. 固体火箭推进技术发展趋势及关键技术分析[J]. 弹箭与制导学报, 1999, 1(1): 53-56 Kou Junqiang. The Development Trend and Key Technology Analysis of Solid Rocket Propulsion Technology[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 1999, 1(1): 53-56 (in Chinese)

[2] 郑军. 灵活机动、便捷高效的固体弹道导弹[J]. 兵器知识, 1999, 2(10): 31-33 Zheng Jun. Flexible, Convenient and Efficient Solid Ballistic Missiles[J]. Ordnance Knowledge, 1999, 2(10): 31-33 (in Chinese)

[3] 宋征宇. 从准确、精确到精益求精——载人航天推动运载火箭制导方法的发展[J]. 航天控制, 2013, 31(1): 4-10 Song Zhengyu. From Accurate, Precise to Perfect——Manned Space Promotes the Development of Guidance Method on Launch Vehicle[J]. Aerospace Control, 2013, 31(1): 4-10 (in Chinese)

[4] Lu P, Pan B F. Highly Constrained Optimal Launch Ascent Guidance[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(2): 404-414

[5] Huang P X, Wei C Z, Gu Y B, et al. A Symplectic Optimization Method for Rapid Endo-Atmospheric Ascent Trajectory Planning[J]. International Journal of Modelling, Identification and Control, 2015, 24(3): 196-205

[6] Mounir K Z, Denis A, Christophe L. Mixed Iterative Algorithm for Solving Optimal Impulsive Time-Fixed Rendezvous Problem[C]∥AIAA Guidance, Navigation, and Control Conference, 2010, Toronto, Ontario Canada

[7] Jing W X, Zheng X, Wei P X, et al. An Ascent Iterative Guidance Algorithm for Solid Rocket Concerned with Multi-Constraints[C]∥27th Chinese Control and Decision Conference (CCDC), 2015, Qingdao, China

[8] 茹家欣. 液体运载火箭的一种迭代制导方法[J]. 中国科学(E辑:技术科学), 2009, 39(4): 696-706 Ru Jiaxin. An Iterative Guidance Method for Liquid Rocket[J]. Science in China(Series E), 2009, 39(4): 696-706 (in Chinese)

[9] 傅瑜, 陈功, 卢宝刚,等. 基于最优解析解的运载火箭大气层外自适应迭代制导方法[J]. 航空学报, 2011, 32(9): 1696-1704 Fu Yu, Chen Gong, Lu Baogang, et al. A Vacuum Adaptive Iterative Guidance Method of Launch Vehicle Based on Optimal Analytical Solution[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(9): 1696-1704 (in Chinese)

[10] 郑伟. 地球物理摄动因素对远程弹道导弹命中精度的影响分析及补偿方法研究[D]. 长沙：国防科学技术大学, 2006: 123-126 Zheng Wei. Research on Effect of Geophysical Disturbance Factors and the Compensation Method for Hit Accuracy of Long-Range Ballistic Missile[D]. Changsha, National University of Defense Technology, 2006: 123-126 (in Chinese)

An Optimal Iterative Guidance Method Based on Exoatmospheric Analytical Dynamic Model

Zheng Xu,Gao Changsheng, Chen Erkang, Jing Wuxing

(Department of Astronautics Engineering, Harbin Institute of Technology, Harbin 150001, China)

The large perturbation deviations of engine parameters of solid rocket would appear in the process of actual flight, which is hard to guarantee superior guidance precision and even causes divergency. Additionally, a large amount of calculation would emerge in terms of explicit guidance of adopting numerical integration of dynamic model, which is hard to satisfy the requirements of the actual flight. To solve the problems, this paper presents an optimal iterative guidance method based on exoatmospheric analytical dynamics model. On the basis of flight dynamics model, the thrust control method of the most-saving fuel is deduced based on the Pontryagin maximum principle, and the iteration guidance algorithm whose iterative variables are conjugate state vector and flight time is given under the condition of a variety of terminal constraints. The iterative guidance precision is analyzed by simulation in the case of maximum positive and negative deviation concerned with solid rocket engine parameters and initial state, followed by monte carlo targeting simulation. The simulation results demonstrate that the proposed iterative guidance method based on exoatmospheric analytical dynamics model displays less computation, high precision, strong robustness and superior engineering application.

solid rocket; iterative guidance method; analytical solution; Pontryagin maximum principle; Monte Carlo targeting

2016-04-01

郑旭(1988—),哈尔滨工业大学博士研究生，主要从事飞行动力学、制导与控制的研究。

V448.131

A

1000-2758(2016)06-1093-08