快速鲁棒性非线性尺度不变的特征匹配算子

张岩, 李建增, 李德良, 杜玉龙

(军械工程学院, 河北 石家庄 050003)

快速鲁棒性非线性尺度不变的特征匹配算子

张岩, 李建增, 李德良, 杜玉龙

(军械工程学院, 河北 石家庄 050003)

提出了一种快速鲁棒性非线性尺度不变的特征匹配算子(speeded up robust nonlinear scale invariant feature,SURNSIF),通过检测子非线性尺度空间的快速求解去除了噪声,同时保证了图像边缘细节,并将自适应选取尺度空间组数、adaptive and generic corner detection based on the accelerated segment test(AGAST)与框状拉普拉斯滤波器去除边缘响应相结合,兼顾了检测的准确性与实时性;描述子交叠带的构建、规范微分响应与非线性尺度空间约束的引入增强了描绘准确性。通过与scale invariant feature transform(SIFT)、speeded up robust features(SURF)、KAZE、binary robust invariant scalable keypoints(BRISK)、AGAST以及快速海森(fast-Hessian)的实验对比,SURNSIF的5种变换鲁棒性均较强,同时速度也更快,综合性能较KAZE提高约10.87%,速度提高约47%。

特征匹配;SURNSIF;KAZE;AGAST

图像匹配是将不同时间、不同视角、相同或不同传感器获取的同一地区的2幅或多幅影像进行空间上对准的过程。其主要解决视点、模糊、照度、JPEG压缩,尺度以及旋转变换问题[1],总体分为基于特征与基于灰度两大类[2]。在利用像素方面,特征匹配比基于灰度信息减少了运算点数目,从而大大减少了匹配的计算量;同时特征匹配对位置比较敏感,从而提高了匹配精度;在特征提取过程中,该类方法减弱了噪声、照度、图像变形及遮挡的影响,并且同名点坐标可以直接估计图像之间的空间变换关系。由于以上的优势,该类算法近些年来被广泛使用与研究[3]。

Lowe于1999年提出了经典的scale invariant feature transform(SIFT)[4]算法,并于2004年对该算法进行了进一步完善。该算法在高斯差分尺度空间(difference of Gaussians,DoG)内检测极值点,并剔除对比度低的点及边缘响应,同时建立梯度方向分布直方图,生成128维描述符。该算法具有尺度与旋转不变性,同时对视点、模糊、照度与JPEG压缩等变换鲁棒性强,但实时性不高。2006年,Bay等人改进了SIFT,提出了speeded up robust features(SURF)算法[5]。该算法使用不同尺寸快速海森矩阵检测关键点,同时利用小波响应生成64维描述符,使得检测与描述速度大幅提升,但对模糊、照度与JPEG压缩等变换敏感。2011年,Leutenegger改良了binary robust independent elementary features(BRIEF)算法[6],提出了binary robust invariant scalable keypoints(BRISK)算法[7]。该算法在近似尺度空间中利用adaptive and generic corner detection based on the accelerated segment test(AGAST)检测特征点[8],同时利用长距离迭代法为特征点赋予方向,并在关键点周围利用固定的采样模式生成二进制描述符。该算法不仅具有视点、模糊、照度、JPEG压缩、旋转与尺度等不变性,而且完全满足实时性要求,但与SIFT、SURF等算法相比,各方面鲁棒性较弱。2011年,Alahi等人提出一种基于人眼视网膜的fast retina keypoint(FREAK)描述子[9]。其本质也是二进制描述符,利用扫视匹配搜索,比BRISK描述符的各种变换鲁棒性均有提高,而且速度完全满足实时需求,但各方面鲁棒性还是较弱。Pablo等人于2012年提出一种非线性特征检测的KAZE算法[10]。传统基于线性高斯金字塔进行多尺度检测的算法都是以牺牲局部精度为代价,来提取特征点同时消除噪声,这容易造成边界模糊和细节丢失,使匹配稳定性差与误匹配点多,非线性尺度分解有望解决此类问题[11]。KAZE的描述子与检测子都是基于SURF而改进设计的,采用任意步长来构造稳定的非线性尺度空间,同时考虑了子区域交叠带,使得对于各种变换比SIFT更为稳健,但速度大幅下降。2013年,Pablo等人又提出一种快速的accelerated-KAZE算法[12]。该算法利用fast explicit diffusion(FED)数学框架,动态加速了非线性尺度空间的计算,同时提出一种二进制描述符modified-local difference binary(M-LDB),使得算法的速度大大提高,但描述子各方面鲁棒性弱于KAZE描述子。

传统特征匹配算子存在问题有:高斯尺度空间无法同时消除噪声并保持图像细节;DoG或快速海森矩阵等的检测速度无法满足实时性需求;尺度空间组数与层数的选取无法满足不同图像处理;去除边缘响应的算法实时性不高;网格性描述子过分分割了空间,打破了图像的连续性;基于小波响应的描绘力较弱,同时并未考虑景深问题。所以欲改良传统特征匹配算子的鲁棒性与实时性问题,其重点是解决尺度空间的构建、检测算子的选用、去除边缘响应算法速度的提高、交叠描述、描述响应的选用与景深描述的问题。

1 算子概述

本文提出了一种快速鲁棒性非线性尺度不变的特征匹配算子(speeded up robust nonlinear scale invariant feature,SURNSIF),该算子包含检测子和描述子两部分,其构成如图1所示。

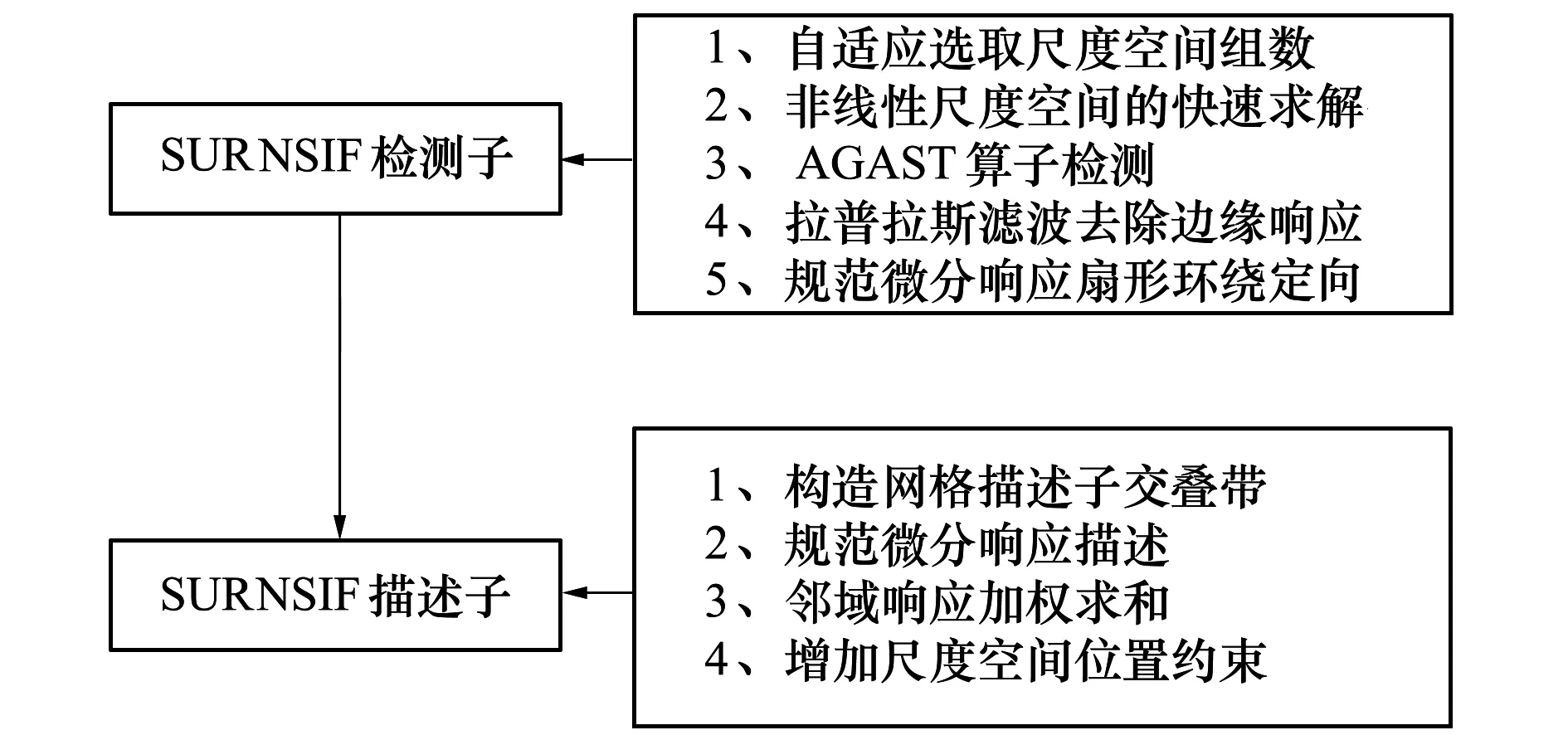
图1 SURNSIF算子示意图

1) 自适应选取尺度空间组数来满足不同图像的检测。

2) 快速求解非线性尺度空间以去除噪声,同时保证边缘。

3) 引入AGAST来提高检测的速度与鲁棒性。

4) 引入框状拉普拉斯滤波器以提高边缘响应去除的速度与准确性。

5) 构建网格交叠带来增强描绘的准确性。

6) 引入规范微分响应与邻域响应加权求和以改善对于模糊、照度以及旋转变换鲁棒性。

7) 增加尺度空间位置约束来增强反映特征点在图像中的灰度关系以及景深关系。

2 SURNSIF特征检测子

2.1 非线性尺度空间建模

非线性扩散滤波方法可以通过非线性偏微分方程来描述：

(1)

c(x,y,t)=

(2)

所选择的c函数能够有效保留边界信息同时平滑区域内部。对比度因子k能控制扩散程度,边缘信息保留量与其负相关,经过大量实验,其值取为图像的梯度直方图70%百分位上的值。

2.2 自适应选取尺度空间组数

为了提高对不同图像检测的准确度与效率,本文提出了适应选取尺度空间组数的方法,其原理如下:

构造尺度级别按对数递增的尺度空间,尺度参数σi如(3)式所示

σi(o,s)=σ02o+s/So=0,1,…,O-1,

s=0,1,…,S-1 i=0,1,…,N

(3)

式中,o表示组,s表示层,σ0表示尺度参数的初始值,O为总组数,S为总层数。N=O×S为尺度空间包含的图像总数。

过大的O与S会导致构造线性尺度空间耗时较长,过少的O与S会导致匹配率下降。经过大量实验,将S定为经验值4,然后根据图像尺寸来自适应选取O,公式如下

(4)

式中,c与r分别表示图像的行数与列数,[]表示取整(四舍五入)。

2.3 非线性尺度空间的快速求解

传统正向欧拉法求解非线性扩散方程时,由于迭代步长太短导致计算复杂。针对上述问题,本文拟采用FED算法[12]求解非线性扩散方程,此方法可以采用任意步长来构造稳定的非线性尺度空间,并且运算快捷。FED算法是通过因数分解盒子滤波器进行动态循环加速,而达到快速求解非线性系统的目的,其原理如下:

根据尺度参数σi按(5)式求出进化时间:

(5)

然后从因数分解盒子滤波器得到不同步长τi来执行显式扩散步骤,τi按(6)式求得,(7)式为该非线性偏微分方程的解:

Li+1,j+1=(I+τjAl(Li))Li+1,jj=0,…,n-1

(7)

式中,I表示单位矩阵,Al为传导运算符,n表示显性扩散步数,τi表示对应步长,τmax表示满足条件的最大步长。

构建非线性尺度空间的流程为:首先对输入图像进行高斯滤波,然后为得到对比度参数k求出梯度直方图,最后由一组进化时间求解隐式差分方程即可得到非线性尺度空间的所有图像。图2为高斯与非线性尺度空间效果对比。

图2 尺度空间对比图

2.4 AGAST算子检测

AGAST改进了features from accelerated segment test(FAST)算法[13],进一步提高了检测效率,与KAZE的海森矩阵检测法相对比,该算法大大提高了速度,同时保证了效果[8]。其本质是有足够多的像素点,其灰度值小于或大于周围邻域内待检测点,则该点被认定为特征点。模板是以待检测点为圆心,半径为3个像素的Bresenham圆。经Rosten测试,阈值定为9的检测稳定性与速度综合性能最优,此阈值可以很快排除伪角点。

然后将AGAST9-16(圆周上共有16个像素,阈值为9)算子应用于非线性尺度空间每一层,并记录下候选点所在非线性尺度空间位置(o与s),求出候选点及其AGAST分数V。

2.5 边缘响应的去除

比较候选点与相邻的上下尺度层中的9×2个点以及同尺度的8个相邻点的AGAST分数V,若所有相邻点的分数均小于该点,则保留该点。这种方法检查效率极高,因为大部分候选点在开始几次检测中就被剔除了。

经过上述步骤,不稳定点和局部极值点均已排除,但仍存在一些边缘点,这对特征点的选取影响极大。本文选用拉普拉斯剔除法来去除边缘响应,通过对应尺度的5×5框状拉普拉斯滤波器对候选点进行处理,如果邻域内各像素点灰度的拉普拉斯值不为0,则保留该点。这种方法比SIFT计算海森矩阵的迹与行列式[4]更快,且准确度更高。

然后经过亚像素级矫正[15]步骤完成特征点的定位。最后为使特征点检测子具有旋转不变性,通过规范微分响应[16]按扇形环绕的方法[5]赋予每一个特征点方向特征。

3 SURNSIF特征描述子

3.1 构造网格描述子交叠带

近年来,描述子的构建方式主要有2种:网格式与二进制式,二者各有优缺点,网格式更准确,二值式更快捷。由于本实验更注重准确性,所以采取网格的方式构建描述子,SIFT、SURF等网格式描述子的描绘方式会包含更加丰富的信息,因此网格描述子比二进制描绘器具有更强的独特性[15,17-18]。

网格描述子容易过分分割了空间,打破图像的连续性。为解决此问题,可在选用网格描述子的同时,构建描述子交叠带。即以特征点为中心,以24S(S为该特征点对应的尺度)为边长,确定一个正方形邻域,如图3所示。

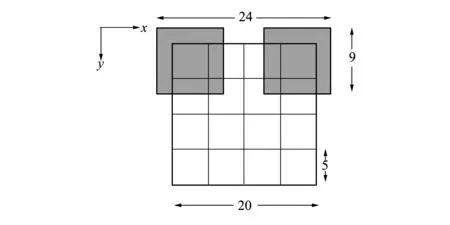
图3 构建描述子向量示意图

将该正方形区域分成16个子正方形区域(横纵各4个),大小为9S×9S,子正方形区域相邻有宽度为2S的交叠带,这样的设计会使交叠带被充分考虑,减小网格描述子分割空间影响,模板描绘更加准确。

3.2 规范微分响应描述

为改善描述子的鲁棒性,引入规范坐标系下的微分响应Lww与Lvv[16],规范微分响应是计算机视觉中十分重要的工具,在尺度变换下能够保持极好的旋转不变性;在不同尺度下,Lww能够测量模糊变换的相关信息,同时Lvv具有良好的边缘响应,所以规范微分响应对模糊具有较强的鲁棒性,它与小波响应的关系如(8)式所示。在每一个子块区域中用模板尺寸为2S的Haar小波滤波器进行处理,得到相对于特征点方向的水平与竖直方向小波响应dx与dy,以及二阶小波响应dxx、dxy与dyy,从而求得规范微分响应Lww与Lvv。

(8)

3.3 邻域响应加权求和

对规范微分响应Lww、Lvv、|Lww|与|Lvv|求和,得到一个4维向量V(∑Lww,∑Lvv,∑|Lww|,∑|Lvv|)。将Lww、|Lww|分为Lvv<0,Lvv≥0 2种情况求和,相应的在对Lvv、|Lvv|求和时分成Lww<0,Lww≥0 2种情况,把4×4个子块区域的向量连起来就得到了4×4×4×2=128维的描述向量。虽然规范微分响应具有照度不变性,但考虑尺度影响,所以将描述向量归一化成单位向量,使描述子具有照度不变性。

由于规范微分响应本质上是加权的Lww梯度函数,权重与图像结构密切相关,所以不需要进行高斯加权处理,这便减少了高斯加权运算的代价,提高了运行速度。规范坐标系具有旋转不变性,因此只需旋转网格即可保证描述子的旋转不变性。

3.4 增加尺度空间位置约束

4 实验验证

4.1 实验设置

1) 实验平台参数

笔记本计算机配置:处理器为Intel酷睿双核i7第4代,主频为2.5GHz。操作系统为Win10 64位系统,编程环境为Visual Studio 2010 与OpenCV 2.41(KAZE与AGAST是由OpenCV 3.10中提取加载的)。

2) 数据集

为体现检测子所产生的不同效果,同时保证实验的客观性,本实验采用Mikolajczyk 05标准测试图集[19](http:∥www.robots.ox.ac.uk/～vgg/research/affine/),如图4所示,该数据集分为8个数据子集(含图像间的单应矩阵),包括5种变换:视点变换、模糊变换、照度变换、JPEG压缩,以及尺度变换和旋转变换。

3) 实验对象及OpenCV相关参数设置

对比近年来较有特点的检测子与描述子:

SIFT: 检测子:组数:4,层数:4,对比阈值:0.04,边缘阈值:10,σ=1.6。

描述子:128维。

SURF: 检测子:fast-Hessain:0.6,组数:4,层数:4,主方向不固定。

描述子:64维。

KAZE: 检测子:组数:4,层数:4,扩散系数:G2,阈值:0.001,主方向不固定。

描述子:64维M-SURF与128维M-SURF。

BRISK: 检测子:阈值:30,组数:4。

描述子:512bit的二进制串,格局规模:1。

AGAST检测子: 灰度阈值:30,进行非极大值抑制,模板:9-16。

fast-Hessian检测子:阈值:600。

图4 测试所用图片集

4) 实验过程和评估准则

通过测定检测子的复现率[19](区域重叠错误率低于40%)、描述子的查全率(recall)和错误率(1-precision)[20](SURF检测子(hessianthreshold:600)与基于欧氏距离的暴力匹配中的半径匹配方式)、运行时间以及遥感影像间的正确匹配率[21]来评判配准算法性能。

4.2 实验结果与分析

4.2.1 SURNSIF检测子的性能

如图5所示,衡量SURNSIF检测子的实验结果分析如下:

1) KAZE与fast-Hessian的对比说明,非线性滤波器构建尺度空间对检测响应在视点、尺度与模糊变换的特征检测性能有大幅度提升。

2) KAZE与SURF的检测结构相似,且确定特征点主方向的方法相同,仅尺度空间的构建不同,所以二者对比说明,各种变换非线性尺度空间较线性尺度空间鲁棒性均有明显提升。1)与2)也正是将非线性滤波器引入SURNSIF的重要原因。

3) AGAST与fast-Hessian的对比说明,AGAST在照度、模糊、视点与JPEG压缩变换方面的鲁棒性都有较大提升,这是将AGAST引入SURNSIF的重要原因。

4) 虽然BRISK中有关尺度空间的构建和方向的确定等都是近似估计的运算,5种变换鲁棒性最弱,但尺度与视点变换较AGAST均有提升,验证了将AGAST引入尺度空间检测的合理性。

5) SURF与SIFT的旋转变换的对比说明,小波扇形环绕特征方向确定法要优于梯度直方图统计法,所以SURNSIF使用小波扇形环绕法确定特征方向。

6) 由于SURNSIF非线性尺度空间构建与AGAST配合时性能比较优良,同时通过框状拉普拉斯滤波器去除了边缘响应,所以照度、模糊、视点与JPEG压缩变换的鲁棒性最高。

7) 由于SURNSIF自适应选取非线性尺度空间组数,所以尺度变换的鲁棒性最高。

8) 由于SURNSIF与KAZE确定主方向方法一致,但规范微分响应在尺度变换下比小波响应更能保持较好的旋转不变性,所以SURNSIF的旋转变换鲁棒性更高。

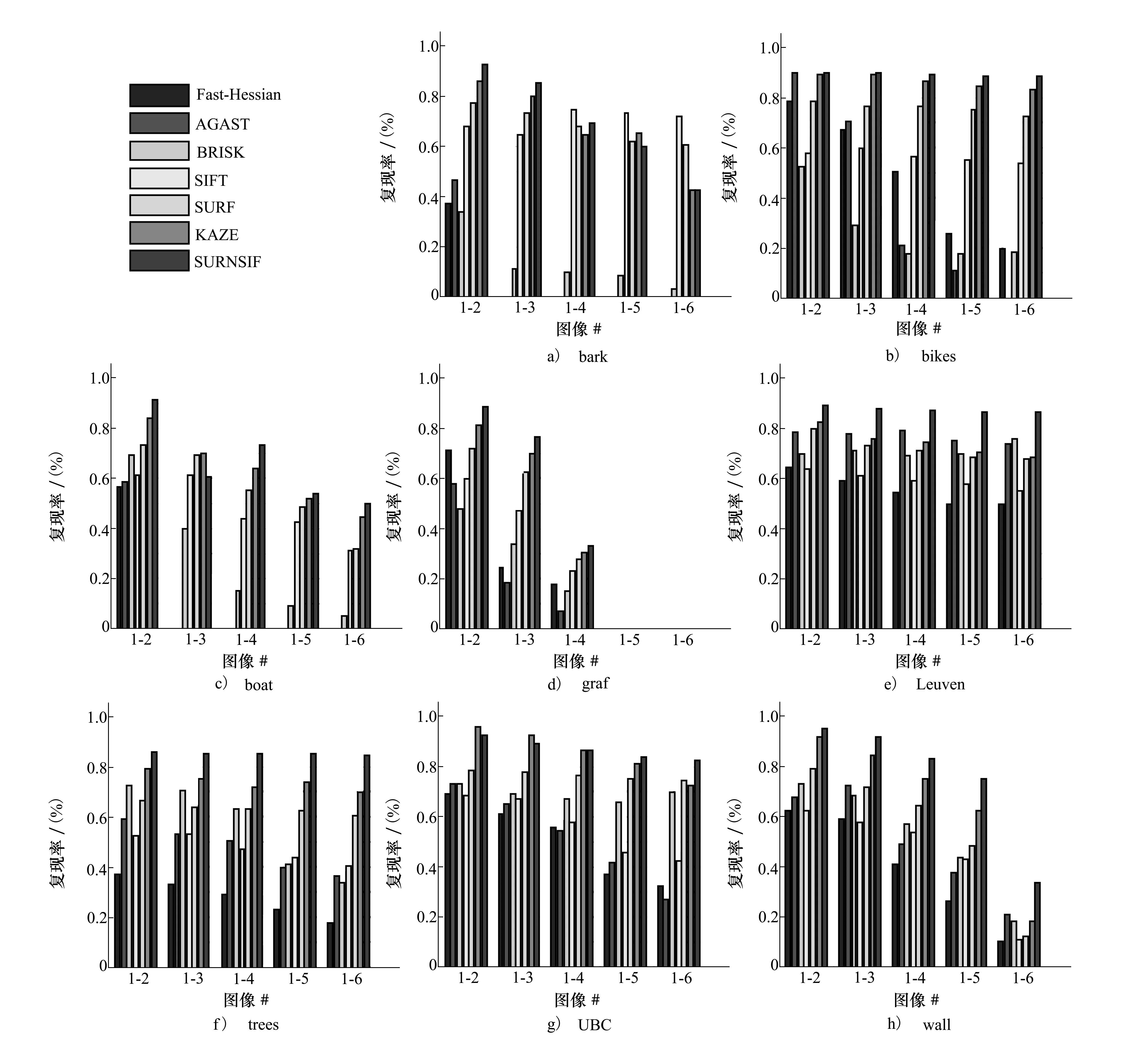
图5 不同变换条件下的复现率比较

综上所述,SURNSIF检测子在视点、模糊、照度、JPEG压缩、旋转与尺度的变换下,均具有良好的鲁棒性,综合性能较KAZE提高约5.76%。

4.2.2 SURNSIF描述子的性能

如图6所示,对每个数据子集中的第1与第4张图像进行测试(曲线采样点数为1 000),衡量SURNSIF描述子的实验结果分析如下:

1) SURF与BRISK的比较说明,二进制特征描绘器的描绘力较弱,这是因为同一采样点参与多次比较导致二进制描述子的部分因信息相关而冗余,所以BRISK描述子5种变换鲁棒性不强,特别是旋转变换鲁棒性较弱。

2) SURF与SIFT的比较说明,在尺度、旋转、视点和JPEG压缩变换下,采用小波特征进行描述操作的鲁棒性较梯度累积均有提升,但在模糊与照度变换下,归一化后小波响应对图像灰度的描绘力不如梯度累积响应强。在小波基础上推导的规范微分响应,比小波响应更适合构建描述子,仅响应不同其余结构相同的G-SURF描述子,较SURF描述子各鲁棒性均有提升,特别是对于模糊变换以及大尺度变换下的旋转变换[18]。

3) KAZE-64与SURF描述子结构相似,相邻子区域交叠的构建不同,所以二者对比说明了相邻子区域的交叠会使描述具有连续性,5种变换鲁棒性均明显提升。

4) KAZE-128与KAZE-64的比较说明了128维M-SURF描述子较64维M-SURF描述子各鲁棒性均有提升。

以上4点正是SURNSIF采用网格式描述子与规范微分响应、引入交叠带以及使用128+2维描述结构的重要原因。

5) SURNSIF与KAZE-128在尺度与视点变换的对比说明,利用尺度空间组与层的对应关系对特征点匹配进行约束以及利用尺度归一化为尺度金子塔定向,可以使约束更为准确,所以提升了尺度与视点变换的鲁棒性。

6) 在照度、模糊与旋转变换方面,SURNSIF与KAZE-128描述结构基本相同,但描述响应不同,因而对于以上3种变换,规范微分响应比小波响应鲁棒性更强,证明了SURNSIF引入规范微分响应的合理性。

7) 规范微分响应对小波响应JPEG压缩的改善较小,所以SURNSIF与KAZE的JPEG压缩变换鲁棒性几乎一致。

综上所述,SURNSIF描述子无论在视点、模糊、照度还是尺度变换的情况下,均具有强鲁棒性,综合性能较KAZE-128提高约4.84%。

4.2.3 时间测试

这一节将对特征检测子与描述子的运行时间进行测试分析。利用SIFT、SURF、KAZE、BRISK、AGAST、fast-Hessian与SURNSIF算法,分别对Graf图像序列中的第1、2张图像(图像大小:800×640 像素)进行实验(次数超过100次),取均值后对比分析SURNSIF的速度特点与优势。

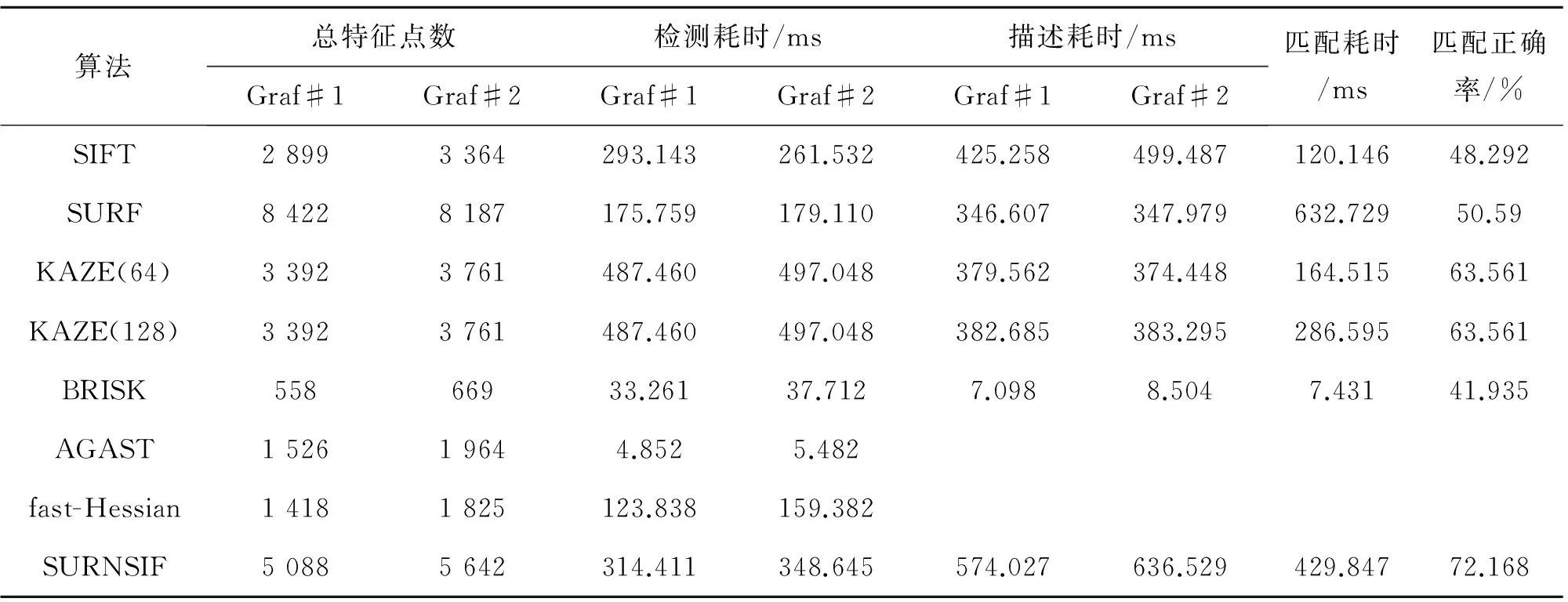
表1 算法耗时比较

表1展现了SURNSIF的速度优势:

1) 检测子方面:因为SURNSIF中引入FED算法加速了尺度空间的构建、引入AGAST与框状拉普拉斯滤波器加速了特征点的检测,所以执行速度大大领先于KAZE与SIFT,但非线性尺度空间构建与定向的计算量远大于SURF的不同尺寸框状滤波器的计算量,所以平均每点速度远低于SURF,与BRISK接近。尺度空间的简化与AGAST的引入共同形成了BRISK的速度优势,说明了AGAST用于提高检测速度的合理性。

2) 描述子方面:SURNSIF的描述子构建思想与SURF类似,但为了提高描绘力,求取规范微分响应、构建相邻子区域交叠带与引入尺度空间约束增加了计算量,所以速度约为SURF的60%。通过KAZE(64)与KAZE(128)的对比可以发现,128维与64维描述子的构建时间相差不多,但匹配时间超出74%。由于KAZE(128)没有求取规范微分响应或引入尺度空间约束,所以速度稍领先于130维的SURNSIF。由于SIFT的描述方式为梯度方向累加,所以耗时最长,SURNSIF较SIFT平均每点速度提高约33%。BRISK速度最快,是因为它的描述子结构为512bit的二进制串,可以按位异或匹配,所以匹配速度也随之变快,但由上节描述子对比结果可知二进制特征描绘器的描绘力较弱,不适合非同源遥感图像的处理。

综上所述,SURNSIF平均每点的检测描述总速度较KAZE提高47%,较SIFT提高40%,约为SURF的35%,BRISK的33%,并且是OpenCV在实现方面对SIFT、SURF、KAZE、BRISK进行优化加速的结果。随着基于OpenMP与OpenCL的并行实现、代码优化与GPU的硬件加速,SURNSIF速度将进一步提高。

4.2.4 基于SURNSIF的遥感影像匹配测试

基于SURNSIF进行遥感影像的匹配测试,同时也为SURNSIF的工程实践提供一种思路。匹配算法流程如图7所示。

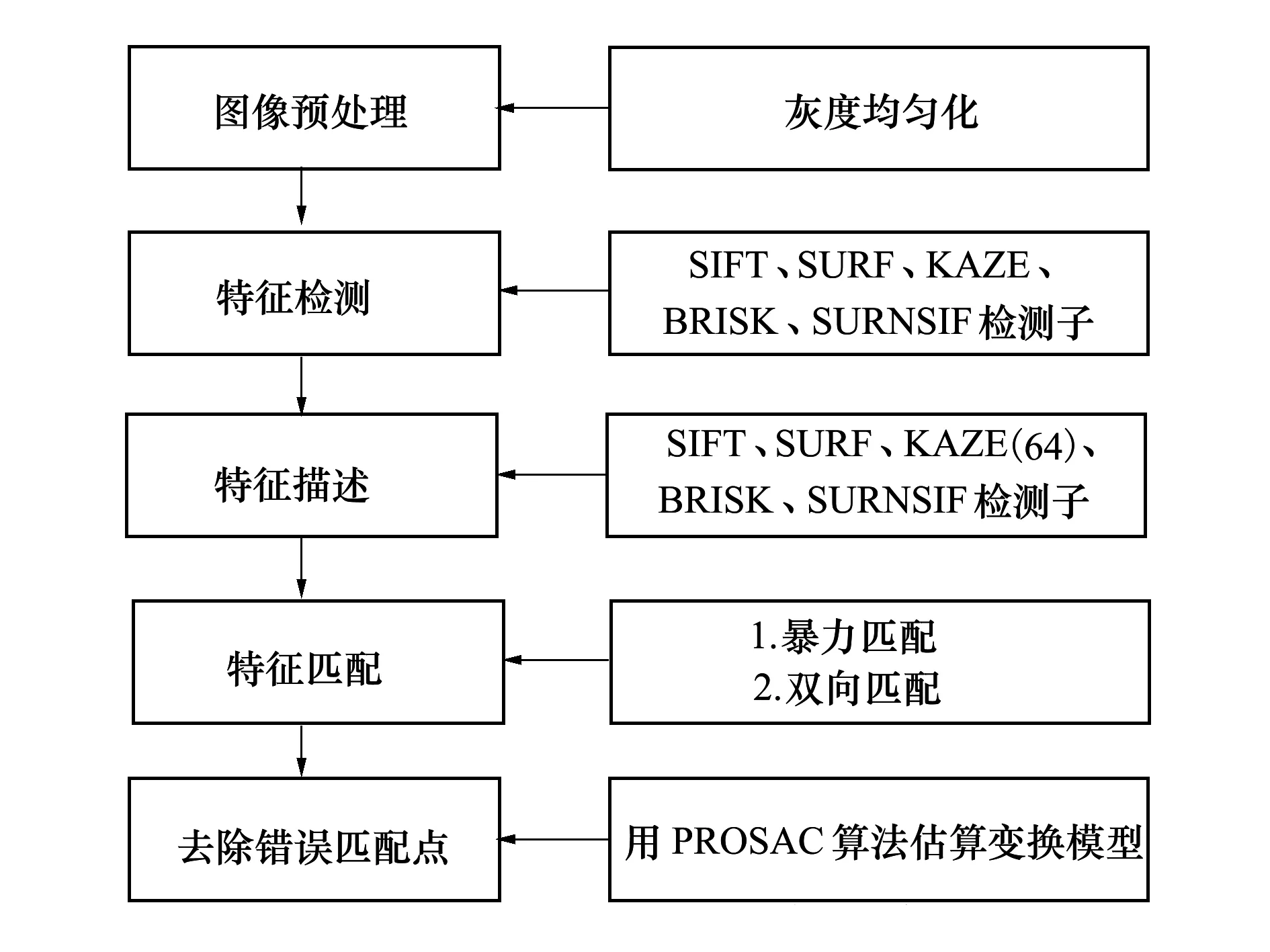
图7 算法示意图

首先利用灰度均匀化减弱光照影响,其次进行特征检测与描述,再次利用暴力匹配方法与双向匹配结合的匹配方法提高搜索效率,最后利用progressive sample consensus(PROSAC)[22]去除外点完成匹配。

本实验利用六旋翼无人机作为实验平台对河北省石家庄市行唐县地区进行了实验,同时与SIFT、SURF、KAZE以及BRISK算子进行了对比。实验主要技术参数如表2所示,航摄影像、谷歌卫星影像拍摄时间约相差6个月,图像分辨率约相差30%,光照条件相差极大,部分影像旋转角度超过180°,视点变化较大、均有运动模糊、噪声影响,对其中4条航带进行实验。

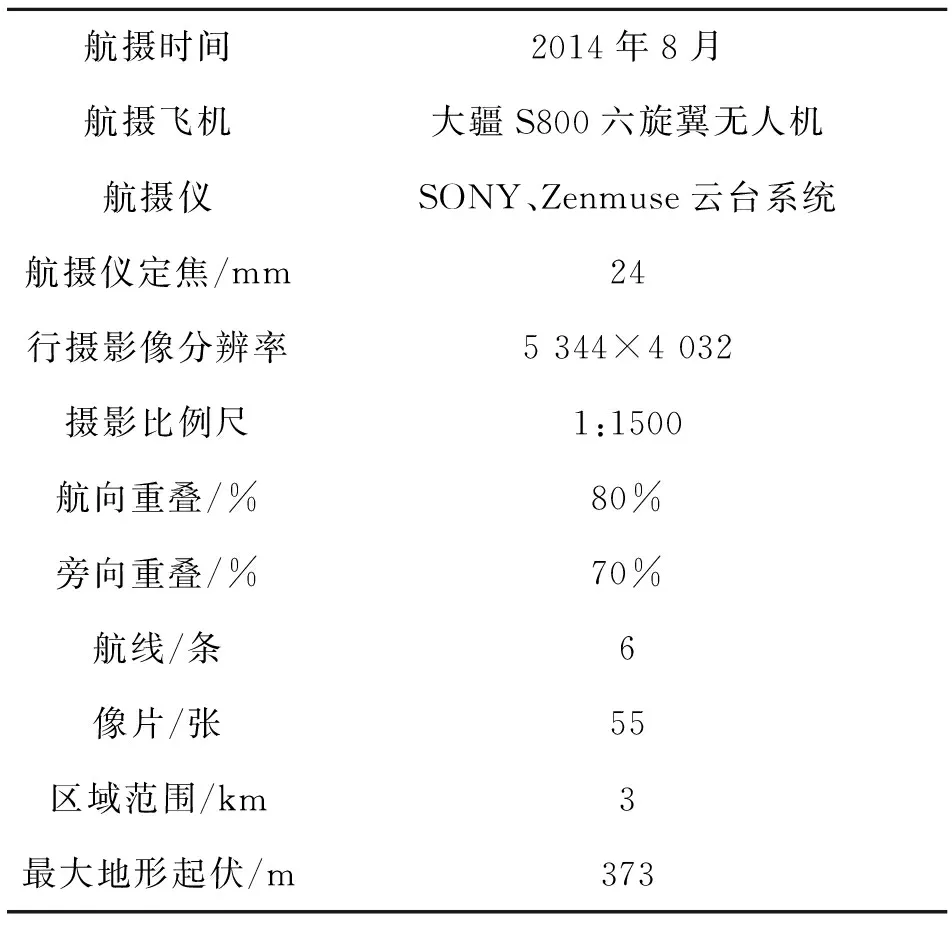
表2 实验影像主要技术参数

图8 配准结果

如图8所示,彩线为同名点连线,黑框为航摄影像透视变换结果,将40组匹配实验结果分析如下:

1) 由于简化近似的检测结构与二进制描述结构,BRISK并不适用于此类照度与模糊程度,特别是旋转角度相差较大的非同源遥感图像匹配,其平均正确匹配率较低,为13.55%,但速度极快。

2) KAZE的平均正确匹配率最高,为49.17%,且较为稳定,特别是针对视点、旋转与尺度变换部分表现出较好的鲁棒性,这得益于非线性尺度空间的构建与交叠带的设计,但实时性不高。

3) SIFT的平均正确匹配率为25.35%,虽然整体上稍逊色于KAZE与SURF,但在照度与模糊变化大时,表现了较好的旋转鲁棒性,这得益于去除边缘响应与梯度直方图统计法的照度鲁棒性高,但同样实时性不高。

4) SURF可适用于非同源遥感图像的匹配,平均正确匹配率介于SIFT和KAZE之间,为26.13%,且速度大幅度提升,完全满足实时性的需求,但对于模糊与照度变换较为敏感。

5) SURNSIF的平均正确匹配率为56.13%,且稳定性与速度均高于KAZE,这是因为SURNSIF构建了非线性尺度空间,然后用AGAST进行检测,最后通过框状拉普拉斯滤波器剔除了边缘响应,增强了尺度、模糊与视点变换鲁棒性,并且考虑了相邻子区域的交叠问题,使得描述具有连续性,还引入了规范微分响应,增强了模糊与旋转变换鲁棒性,同时进行了归一化尺度空间位置约束,增强了尺度与视点变换鲁棒性,所以匹配效果较好,且速度较快。

SURNSIF在图像及视频检索、目标识别、纹理识别、数据挖掘、飞行器导航和宽基线匹配等多个领域,具有广阔的应用前景。同时,SURNSIF在实时性要求较高的应用领域具有巨大潜力。

5 结 论

本文提出一种SURNSIF算子,并通过实验验证了算子的可行性与优势,主要做了如下工作:

1) 针对目前特征匹配算子鲁棒性与实时性问题,分析了该问题解决的核心所在,理清了特征匹配算子的研究思路。

2) 通过综合分析里程碑式的特征匹配算子发展历程与优缺点,根据存在的实际问题,提出了SURNSIF算子。并对其检测子与描述子的设计进行了详尽的理论分析与实验验证,通过与当前使用广泛的SIFT、SURF、KAZE、BRISK、AGAST与fast-Hessian算子对比,定量表现了本算法在解决特征匹配5种变换及速度等问题上存在很大优势。

3) 本实验通过六旋翼无人机为平台对河北省石家庄市行唐县地区进行了实验与分析,实验结果有效证明了本方法的特点与优势,为工程实践提供了指导帮助,同时也指明了本算法的发展前景。

本算子未来的改进:SURNSIF检测子交叠带设计与景深关系推导还可以进一步研究,算法可以进行并行设计与增加GPU硬件加速来提高运行效率。

[1] 樊曼曼. 多源卫星遥感影像配准技术研究[D]. 秦皇岛：燕山大学, 2011 Fan Manman. Resarch of Multi-Source Image Matching Technology[D]. Qinhuangdao, Yanshan University, 2011 (in Chinese)

[2] 宋芳, 李勇, 陈勇. 多源遥感图像中的图像配准方法[J]. 激光杂志, 2008, 29(3): 26-27 Song Fang, Li Yong, Chen Yong. Match Methods for Multisensor Remote Sensing Image Registration[J]. Laser Journal, 2008, 29(3): 26-27 (in Chinese)

[3] 廖斌. 基于特征点的图像配准技术研究[D]. 长沙: 国防科学技术大学, 2008 Liao Bin. Feature Aided Target Maneuver Detection Technology[D]. Changsha, National University of Defense Technology, 2008 (in Chinese)

[4] Lowe D G. Distinctive Image Features from Scale-Invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110

[5] Bay H, Tuytelaars T, Van Gool L. SURF: Speeded Up Robust Features[C]∥Proceedings of 9th European Conference on Computer Vision. Graz, Austria: Springer Berlin Heidelberg, 2006: 404-417

[6] Calonder M, Lepetit V, Strecha C, et al. Brief: Binary Robust Independent Elementary Features[C]∥Proceedings of 11th European Conference on Computer Vision Crete, Greece: Springer Berlin Heidelberg, 2010: 778-792

[7] Leutenegger S, Chli M, Siegwart R Y. BRISK: Binary Robust Invariant Scalable Keypoints[C]∥Proceedings of 2011 International Conference on Computer Barcelona, Spain, 2011: 2548-2555

[8] Mair E, Hager G D, Burschka D, et al. Adaptive and Generic Corner Detection Based on the Accelerated Segment Test[C]∥Proceedings of 11th European Conference on Computer, Heraklion, Crete, Greece: Springer Berlin Heidelberg, 2010: 183-196

[9] Alahi A, Ortiz R, Vanderrgheynst P. FREAK: Fast Retina Keypoint[C]∥Proceedings of Computer Version and Pattern Recognition, 2011: 510-517

[10] Pablo F, Adrien B, Andrew J. KAZE Features[C]∥Proceedings of 12th European Conference on Computer Version, Florence, Italy: Springer Berlin Heidelberg, 2012: 214-227

[11] 李鹏, 武文波, 王宗伟. 基于非线性尺度空间的多源遥感影像匹配[J]. 测绘科学, 2015, 40(7): 41-44 Li Peng, Wu Wenbo, Wang Zongwei. Muti-Source Remote Sensing Images Matching Based on Nonlinear Scale Space[J]. Science of Surveying and Mapping, 2015, 40(7): 41-44 (in Chinese)

[12] Pablo F, Jesus N, Adrien B. Fast Explicit Diffusion for Accelerated Features in Nonlinear Scale Spaces[C]∥Proceedings of 2013 British Machine Vision Conference. Bristol, UK, 2013:2157-2163

[13] Edward R, Tom D. Machine Learning for High-Speed Corner Detection[C]∥Proceedings of 9th European Conference on Computer Vision, Graz, Austria, 2006: 430-443

[14] 胡波. 基于颜色不变量的特征匹配算法研究[D]. 沈阳：辽宁大学, 2014 Hu Bo. Study of Feature Matching Algorithm Based on Color Invariant[D]. Shengyang, Liaoning University, 2014 (in Chinese)

[15] 王飞宇, 邸男, 贾平. 结合尺度空间FAST角点检测器和SURF描绘器的图像特征[J]. 液晶与显示, 2014, 29(4): 598-604 Wang Feiyu, Di Nan, Jia Ping. Image Features Using Scale-Space FAST Corner Detector and SURF Descriptor[J]. Chinese Journal of Liquid Crystals and Displays, 2014, 29(4): 598-604 (in Chinese)

[16] Pablo F, Luis M, Andrew J. Gauge-SURF Descriptor[J]. Image and Vision Computing, 2013, 31(1): 103-116

[17] 余淮, 杨文. 一种无人机航拍影像快速特征提取与匹配算法[J]. 电子与信息学报, 2016, 38(3): 509-516 Yu Huai, Yang Wen. A Fast Feature Extraction and Matching Algorithm for Unmanned Aerial Vehicle Images[J]. Journal of Electronics and Information Technology, 2016, 38(3): 509-516 (in Chinese)

[18] 张宝龙, 李洪蕊, 李丹, 等. 一种针对车载全景系统的图像拼接算法的仿真[J]. 电子与信息学报, 2015, 37(5): 1149-1153 Zhang Baolong, Li Hongrui, Li Dan, et al. A Simulation of Image Mosaic Algorithm Based on Vehicle Panorama System[J]. Journal of Electronics and Information Technology, 2015, 37(5): 1149-1153 (in Chinese)

[19] Mikolajczyk K, Tuytelaars T, Schmid C, et al. A Comparison of Affine Region Detectors[J]. International Journal of Computer Vision, 2005, 65(1/2): 43-72 (in Chinese)

[20] Mikolajczyk K, Schmid C. A Performance Evaluation of Local Descriptors[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2005, 27(10): 1615-1630

[21] Winder S A J, Brown M. Learning Local Image Descriptors[C]∥Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis, Redmond, 2007: 1-8

[22] Chum O, Matas J. Matching with PROSAC-Progressive Sample Consensus[C]∥Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Minneapolis, 2005: 220-226

Speeded up Robust Nonlinear Scale-Invariant Feature

Zhang Yan, Li Jianzeng, Li Deliang, Du Yulong

(Ordnance Engineering College, Shijiazhuang 050003, China)

This paper puts forward a speeded up robust nonlinear scale invariant feature(SURNSIF). Noise is wiped off and edge response is guaranteed through the fast solving of nonlinear scale space. Adaptive selection of number of scale space and the Adaptive and Generic corner detection based on the accelerated segment test(AGAST), combined with frame Laplace filter via removing edge response take account of the detection accuracy and real-time performance. Constructing descriptor overlap, introduction of gauge derivatives and the constraint of feature point in the nonlinear scale space location enhance the accuracy. Comparing to scale invariant feature transform(SIFT), speeded up robust features(SURF), KAZE, binary robust invariant scalable keypoints(BRISK), AGAST and fast-Hessian experiments, the SURNSIF reveals stronger robustness with 5 kinds of changes, and its registration speed is faster. Compared with KAZE, comprehensive robustness is increased about 10.87%, and the speed is increased about 47%.

feature registration; SURNSIF; KAZE; AGAST

2016-03-08

国家自然科学基金(51307183)资助

张岩(1991—),军械工程学院博士研究生,主要从事计算机视觉与无人机图像信息处理技术研究。

TP391.4

A

1000-2758(2016)06-1108-12