最小二乘法在纯方位目标跟踪中的应用

吴小强,潘丽丽

(1.海军驻南京地区雷达系统军事代表室,南京210003;2.中国船舶重工集团公司第七二四研究所,南京211153)



最小二乘法在纯方位目标跟踪中的应用

吴小强1,潘丽丽2

(1.海军驻南京地区雷达系统军事代表室,南京210003;2.中国船舶重工集团公司第七二四研究所,南京211153)

从实际的工程应用入手,研究了被动纯方位目标跟踪中方位轨迹滤波算法。分析了目标方位变化情况,建立方位变化模型,采用限定记忆最小二乘法对方位轨迹进行滤波。仿真结果表明,该算法能够降低方位测量误差,是一种较好的工程实用算法。

纯方位目标跟踪;方位轨迹滤波;限定记忆最小二乘法;多项式拟合

0 引 言

对于单站被动雷达,在未定位时能够获得的目标位置信息仅包含方位,并不包括距离。因此,在系统定位之前仅能利用目标的位置信息方位及其属性参数进行纯方位目标跟踪。

在被动雷达多目标跟踪中,跟踪滤波将与航迹正确相关后的量测送入跟踪滤波器进行实时的平滑滤波,并对目标辐射源各参数进行估计更新,能够降低目标方位误差,为系统提供更准确的目标运动轨迹参数。

常用的跟踪滤波算法很多,与其他方法(维纳滤波、α-β滤波器、Kalman滤波等)相比,最小二乘法简单方便,是经典的参数估计方法,且在一定条件下具有良好的统计性,因而更具有工程实现的意义。文中通过建立目标测量方位变化模型,同时考虑实际探测中目标运动的变化,采用限定记忆最小二乘法对方位轨迹进行滤波。

1 最小二乘法

最小二乘法的原理是:测量结果的估计值应使i(i=1,2,…,k)时刻的测量值与真实值之间的误差平方和(或加权误差平方和)最小,即对于量测:

z(i)=h(ti,x)+w(i),i=1,2,…,k

k时刻误差的平方和为

则使J(k)达到最小的参数x的值即为该时刻x的最小二乘估计[1]。下面从向量矩阵角度来讨论最小二乘估计。

假定待定非随机向量X,第i个时刻的量测值为

Z(i)=H(i)X+N(i)

式中,H(i)为量测矩阵,N(i)为量测噪声矩阵,共进行i=1,2,…,k次量测,其k次量测可用下列矩阵方程表示:

Z=HX+N

其中

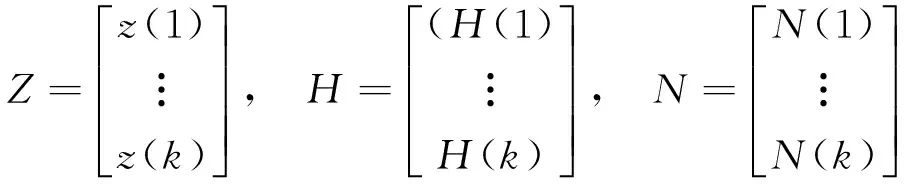
xJ(k)=2(H)T[Z-HX]=0

由上式可得

考虑上述情况,可以对最小二乘滤波的数据长度进行限制,即当前时刻目标量测的估计值仅与现在及此前一段时间内的若干个历史数据有关,而与更远的过去量测没有联系。这种方法称为限定记忆最小二乘滤波[2]。

2 目标方位变化模型

由于单站被动雷达在不进行定位的情况下目标状态的获取是不完全的,因此跟踪滤波主要针对的是目标方位。将方位按泰勒公式展开可得

考虑实际探测中一定时间内目标方位随时间的变化是平缓的、规律的,其变化曲线可以认为是平滑的,可近似认为匀速或匀加速变化,可得如下式所示的目标方位随时间变化模型。

式中,k表示量测周期,t为量测周期的时间间隔。

由上式可知,当观测站和目标存在相对运动时,目标方位变化曲线在一定时间内可近似为多项式模型。对获取的测量方位序列可用多项式进行拟合。这里采用最小二乘法对多项式进行拟合。

上述方位变化模型中,其状态变量表示为

则其状态模型可表示为

X(k+1)=AX(k)+W(k)

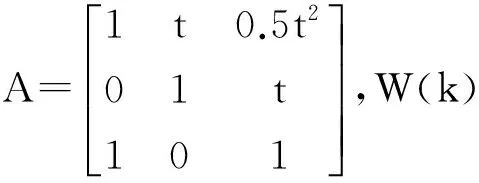
θm(k+1)=CX(k+1)+v(k+1)

其中,C=[1 0 0],v(k)为量测噪声,则

式中v(k+1)为量测噪声。

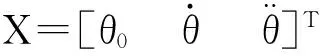
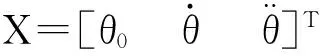
用矩阵形式表示为

Z=HX+V

式中

则该滤波窗口内i(i=k-M+1,…,k)时刻的方位估计值为

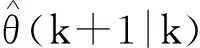
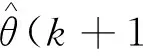
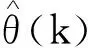
使用限定记忆最小二乘法进行滤波时,其核心问题是确定滤波窗口的大小。窗口的大小可以根据方位变化的经验统计来确定。如果方位变化较大应选择较小的窗口,反之则可选择较大的窗口。通常以滤波阶数为基准,以经验统计来确定参与最小二乘运算的点数。

3 仿真和实测结果分析

为了验证方位轨迹滤波算法的效果,分别对两组仿真数据和实测数据进行了仿真处理分析。

(1) 仿真情况

观测站与辐射源目标站初始距离80 km,观测站以46 km/h、180°方向运动,目标以18.5 km/h速度、90°方向运动,方位方差为0.7,航向方差0.7,航速方差0.1,产生如图1中实线所示的目标方位轨迹。

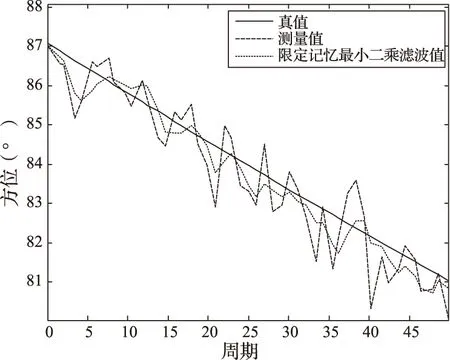
图1 仿真数据方位轨迹图

(2) 实测数据

观测站与目标站初始距离90 km,观测站以40 km/h、126°方向运动,目标以20 km/h速度、225°方向运动,目标方位轨迹真值如图2中实线所示。

对上述目标方位轨迹的测量数据采用限定记忆最小二乘滤波算法进行处理,得到如图1～图4所示的处理结果。而表1为上述两组数据方位误差分析。从上述图表中可以看出,采用限定记忆最小二乘滤波算法的方位轨迹变化更平稳,误差标准差更小。

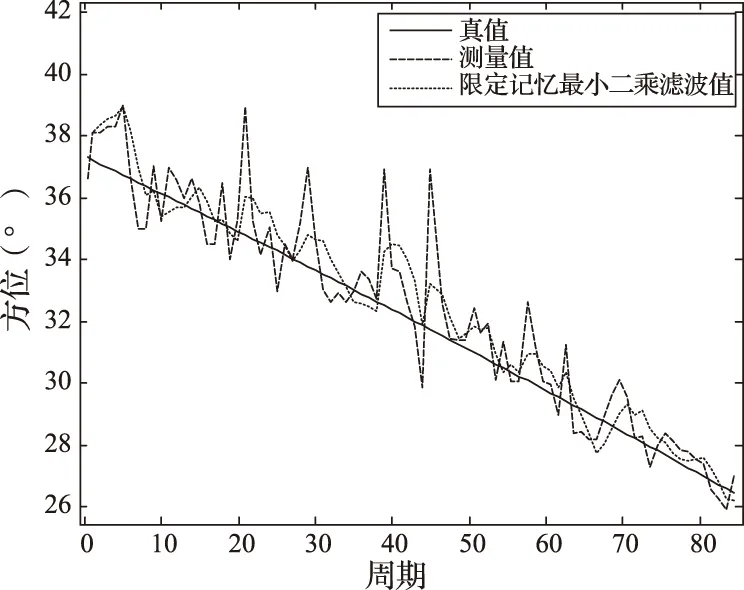
图2 实测数据方位滤波轨迹图

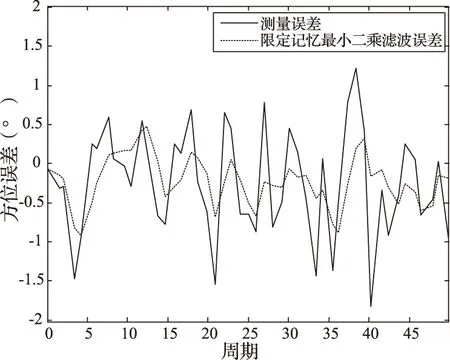
图3 仿真数据方位误差图

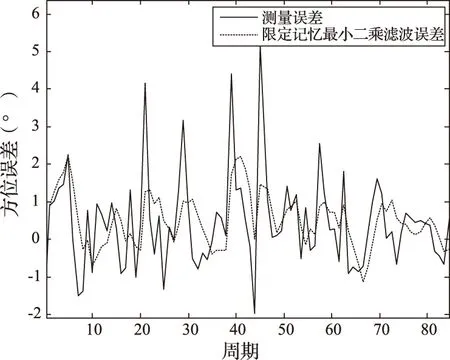
图4 实测数据方位滤波误差图

表1 滤波算法误差分析表

从上述结果可以看出,本文的滤波法能有效提高方位估计精度,降低目标方位误差。

4 结束语

本文从实际工程应用入手,讨论了单站被动多目标方位跟踪滤波的问题。文中建立了目标方位变化模型,采用限定记忆最小二乘法对目标方位进行滤波,且目标方位的滤波估计值仅与当前周期方位及前M-1个周期的方位有关。该算法充分考虑了目标运动状态的变化,降低了对历史方位的依赖,有效提高了方位的估计精度,是一种较好的工程实用型算法。

[1] 何友,修建娟,张晶炜,等,雷达数据处理及应用[M]. 2版.北京:电子工业出版社,2009:21,27-28.

[2] 李健翩,李学仁.多项式拟合在试飞数据预处理中的应用[J]. 弹箭与制导学报,2005,25(4).

[3] 沈凤麟,叶中付,钱玉美. 信号统计分析与处理[M]. 合肥: 中国科学技术大学出版社,2001:365-366.

Application of least square method in bearing-only target tracking

WU Xiao-qiang1, PAN Li-li2

(1.Military Representatives Office of Radar System of the PLA Navy in Nanjing, Nanjing 210003;2. No.724 Research Institute of CSIC, Nanjing 211153)

The bearing track filtering algorithm in the passive bearing-only target tracking is studied from the actual engineering application. The change of the target azimuth is analyzed, and the azimuth change model is established. The azimuth tracks are filtered through the limited memory least square method. The simulation results indicate that the algorithm can reduce the azimuth measurement error, and it is a preferable and practical engineering algorithm.

bearing-only target tracking; bearing track filtering; limited memory least square method; polynomial fitting

2016-04-30;

2016-05-12

吴小强(1971-),男,工程师,研究方向:雷达总体技术;潘丽丽(1979-),女,工程师,研究方向:雷达数据处理。

TN959.6

A

1009-0401(2016)04-0012-03