整合教学资源 实现高效课堂——以“直线与平面垂直”第一课时教学为例

李彦鹏

(宁夏盐池高级中学，751500)



整合教学资源 实现高效课堂
——以“直线与平面垂直”第一课时教学为例

李彦鹏

(宁夏盐池高级中学，751500)

导学案是打造高效课堂的有效载体,是用于指导学生自主学习、主动参与、合作探究的学习方案．但也有一定不足之处,如信息技术应用少,问题相对集中,教师主导性不够,只是一味地让学生讲解,在有限空间里展示，学案预设了问题思路,限制了学生思维空间，等等．教学实践表明,结合学生实际,设计学案导学,有机地整合教学与课程资源,真正体现了先学后教方法,把导与学结合起来,让学生参与到教学活动中,更有利于课堂教学．本文以高中数学(人教版必修2)“直线与平面垂直的判定”第一课时的教学为例,从教学资源有机整合的角度,论述高效课堂的有效性与学生核心素养培养策略．

一、课题引入

教师:几何学是研究现实世界中物体的形状、大小与位置关系的学科,其中位置关系主要是平行与垂直.平行的问题已经解决了,今天我们来研究垂直问题．(教师在黑板上板书课题:直线与平面垂直的判定)

点评因为学生手中有学案,对学习目标与内容已经有所了解,因此,不必要拐弯抹角,可以开门见山,直指课题．教师语言引导与黑板板书有机结合,将学生置于学习目标中,并揭示课题．

二、教学活动

活动1 直线与平面垂直的定义

1.让学生在阅读中学习

教师:下面请大家带着学案上的学习目标阅读课本第64页内容(直线与平面垂直的定义),把重点划出来．

(学生阅读)

点评读书永远是我们学习的基本方法,它体现了以学生为主体的发挥课本优质资源教学活动,这不是导学案在唱主角,也不是跟着多媒体课件在演戏．学生学习知识与课本文本相结合,针对学习内容的特点,不需要解释说明的内容,让学生在阅读中学习更有效．这有利于培养学生阅读能力与抽象概括能力及数学素养．

2.让学生在问题引导下学习

教师:你能举出几个实际生活中线面垂直的例子吗?

学生:旗杆所在直线与地面所在平面垂直,大桥桥柱所在直线与江面所在平面垂直……

(教师用多媒体屏幕展示天安门前五星红旗迎风飘扬中的国旗旗杆)

点评举出生活中的实例,从感性上认识事物.多媒体图片显示与学案呈现问题相结合，直观、醒目,观察思维得到了培养,直观素养得以体现,并且为下面的问题埋下伏笔．

教师:旗杆AB与它在地面的影子BC的位置关系怎样?随时间推移呢?旗杆AB与地面上任意一条不过点B的直线l位置关系又怎样(图1)?

学生:都是垂直的．

(学生回答后,用多媒体演示上面问题的动画过程)

点评随着时间推移旗杆始终与其影子垂直,任意一条不过点B的直线也与旗杆AB垂直．教学中充分发挥多媒体优势,恰当的动画学习更高效．多媒体动画图形或几何画板动画图形和学案呈现问题紧密结合,发现问题与得到结论较容易,难点突破很有效．

教师:你能概括出线面垂直的定义吗?如何正确理解定义?

(小组讨论后,代表发言,其他学生补充.教师再用多媒体展示，学生在笔记中完善定义)

教师板书定义如下：

点评多媒体屏幕展示课本中关于线面垂直的定义,教师发挥主导作用,揭示定义中所包含的2层意思.

学案呈现问题,学生尝试回答与多媒体展示定义,学生修正，教师板书定义与解释深刻含义无缝结合．几何直观与数学抽象相结合，有利于培养学生的思维能力.在问题引导下学习,既要关注学生,也要发挥教师的引导作用,这样的教学更有效．

3.让学生在辨析中学习

教师:下面的命题是否正确？为什么?请小组讨论发言．

(1)如果一条直线垂直于一个平面内的无数条直线,那么这条直线与这个平面垂直；

(2)如果一条直线垂直于一个平面,那么这条直线就垂直于这个平面内的任一直线；

(3) 只要直线a与平面α内有一条直线不垂直,那么直线a与平面α不垂直．

(学生讨论后,回答问题)

点评第(1)问学生根据定义可以辨析清楚,也可以出示反例模型,教师用几何画板动画展示,印象会很深;第(2)问就是定义,加深印象;第(3)由学生举出反例,从另一个角度说明定义,对线面垂直定义理解有较大帮助．学案呈现问题,学生举例,教师几何画板动画展示．以上三个环节一起有序应用,有利于知识的理解与应用．

活动2 直线与平面垂直的判定

1. 让学生在实验中学习

师：如图2,请同学们拿出准备好的一块(任意)三角形的纸片.我们一起来做一个实验:过∆ABC的顶点A将纸片翻折,得到折痕AD,将翻折后的纸片竖起放置在桌面上,(BD、DC与桌面接触)观察并思考:

(1)折痕AD与桌面垂直吗?为什么AD与桌面不垂直?

(过点A做折痕有很多情况,各组学生做了几个折痕,翻折后竖起置在桌面,发现都不垂直,原因由线面垂直的定义也不难想到)

(2)如何翻折才能使折痕AD与桌面所在的平面垂直?为什么AD与桌面垂直?

(一会儿,有几个小组的同学,发现第二个问题答案)．

点评由于实验设计出两个恰当、合理的问题,学生实验操作过程是带着问题观察思考，所以目标很清楚．

学生分组开始实验操作,教师提示:折痕AD要突出任意性,折痕与桌面不垂直的原因可以依据定义分析．其中一个小组代表回答第(1)问：我们小组由3名同学来做实验，其中两名手拿书本平置在空中,另一名学生将折好三角形纸板,放在其书本平台上面,大家可以清楚地观察过程、结果．当且仅当,折痕AD与BC垂直时,翻折后的纸片竖起放置在桌面上(BD、DC与桌面接触)，AD与桌面垂直．另外一个小组也有几名同学积极解答了第(2)问.并合理地解释原因,得出相关的具体结论．教师在此基础上,利用多媒体动画、语音暗示等再现上述实验过程.AD垂直桌面,是由于AD都垂直BD和DC,且相交在一个平面上．当相交直线BD和DC离开D点时,具备上述条件,AD也垂直桌面,因为两条相交直线确定整个平面,再一次给予抽象概括．实现了本节几何教学课程目标:观察、实验、操作、说理等环节．

点评这是本节课的重点、难点之一．课本文本试验问题、学生实验操作、教师多媒体演示,三方面有机结合,完成本节课的重点内容．学生积极参与实验活动,展示暴露学习知识过程,自主发现问题,并自主解决了问题,锻炼动手能力,培养了发现问题、解决问题能力及探究素养．

2.让学生在问题引导下学习

教师:(1)通过实验,你能得到什么结论?

(2)你能概括出线面垂直的判定定理吗?结合图形符号表示．

点评学生语言回答后,师生修改、完善．教师多媒体演示语言叙述的判定定理,多媒体显示图形,提问学生用符号语言描述定理,最后展示屏幕上,学生修改、完善、记忆、理解,培养了学生数学抽象核心素养．

3. 让学生在典型例题中学习

教师:请大家看学案中的两个问题,并画图、思考,尝试如何解决．

(1)如果a∥b,a⊥c，那么b⊥c吗?为什么?

结论:两条平行线中的一条直线与已知直线垂直,那么另一条也与该直线______．

(2)课本例1: 如图3,已知a∥b,a⊥α,求证:b⊥α．

结论:如果两条平行线中的一条直线与一个平面垂直,那么另外一条直线也与此平面______.

点评例题是课本文本的优质资源,充分利用好,能达到应用知识和方法的目的,实现学习目标的途径．学案的设计考虑到,例题既是直线与平面垂直的定义与判定定理的应用,同时可以作为线面垂直判定的一种方法.在证明过程中要用到常用结论:两条平行线中的一条直线与已知直线垂直,那么另一条也与该直线垂直．考虑学生基础不一致,分两步学习例题，首先让学生小组探究,然后展示解题过程.一题多解,其他学生评价,说明解题过程用到的方法,并得到结论,让学生归纳填写．

三、当堂检测

教师:请大家各自独立完成下面的问题：

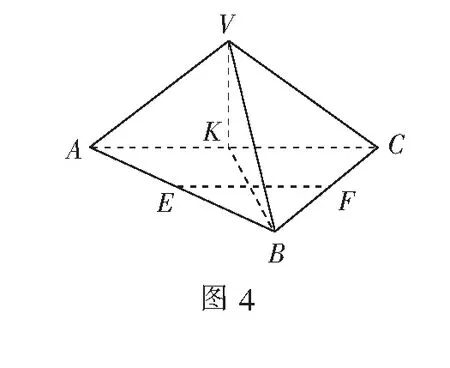
如图4，在三棱锥V-ABC中,VA=VC,AB=BC,K是AC的中点.

(1)求证:AC⊥平面VKB;

(2)求证:VB⊥AC;

(3)若E、F分别是AB、BC 的中点,试判断EF与平面VKB的位置关系.

点评已经历探究,高效的学习过程,还要安排当堂检测,是从学生学的角度,检测学生的学习情况．学生独立完成,上黑板展示解题过程,学生、教师评价．多媒体与学案以及学生板书三者相结合．

四、课堂小结

教师提示:(针对板书内容)今天我们学习了那些内容?(学习了线面垂直的定义与判定定理，板书与多媒体演示结合相结合)

学生活动:回顾小结．

点评一节课,要做到许多教学资源有机结合,需要教师具备深厚的教学功底,在教学中要灵活应用各种资源和掌握先进的教学理念,不断提升专业技术基本能力,这样才能发展和培养学生的核心素养，也才能使课堂教学真正做到高效．