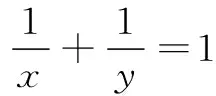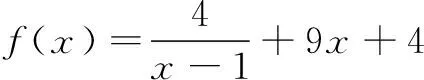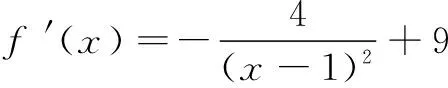高中数学不等式的教学策略

张 兵

(江苏省丰县民族中学，221700)



高中数学不等式的教学策略

张 兵

(江苏省丰县民族中学，221700)

不等关系与相等关系都是刻画现实世界数量之间的相互关系,在高中数学教学中占有重要的地位,同时也是高中数学教学的难点之一.因此,对不等式教学的研究一直受到数学教师的关注．但在实际教学过程中,教师往往侧重于不等式的证明与性质内容的应用,而对在实际问题中引导学生抽象出不等关系的数学模型,建立不等关系的观念的教学重视不够.本文结合个人的教学实践，谈谈自己的一些做法与体会．

苏教版高中课标教材中几乎每一部分内容都涉及不等式的相关内容.例如，求函数的定义域、值域问题,参数取值范围问题，单调性问题;立体几何中涉及线线、线面、面面所成的角问题；一元二次不等式及其解法，二元一次不等式(组)与简单的线性规划问题，基本不等式及利用导数研究单调性、求值域，等等.从中可看出不等式的内容在高中数学教学中的重要性.而学生对不等式的熟练掌握与应用不是一蹴而就的，需要老师在平时的教学过程中渗透不等关系的思想,潜移默化地培养学生利用不等式解决问题的习惯．为了在实际教学中更加有效地使学生理解并正确利用不等式的性质解决问题,个人的做法主要是根据学生的实际情况,设置恰当的教学策略,立足课本、选择恰当的教学模式,依据新课改的精神,引导学生在合作学习中掌握不等式的相关概念、性质；并在此基础上提高学生的利用这些概念、性质解决问题的能力,达到解决问题的目的．

在实际教学中,为了培养学生在解决问题过程中运用不等式的意识,更好地提高学生运用不等式解决问题的思想,培养学生创新的意识,教师应始终把学生的自主学习放到第一位,引导学生自主学习、自我评价、自我巩固，逐步形成运用不等式解决问题的意识,不断提高数学素养．

一、数学结合的思想

华罗庚先生说过:“宇宙之大粒子之微，火箭之速，化工之巧，地球之变，生物之谜，日用之繁，无处不用数学.”数学是一切科学的工具，科学愈发达，需要的数学工具就愈多，哪里有‘形’，哪里有‘数’，哪里也就少不了数学． 数形结合是我们解决问题的重要方法,对数形结合的灵活运用也反映了一个人的数学素养．因此,在不等式教学中,教师要始终处理好数与形的关系,引导学生在解决问题时始终具有两种思想,即通过数学表达式解决问题时,一定清楚其相应的图形;同时在利用图形解决问题时一定清晰其所代表的数学表达式．数形结合的本质一方面是把抽象的问题形象化、具体化、把推理过程简单化；另一方面用代数方法解决问题时避免几何方法解决问题时带来的局限性.两者的完美结合是我们成功解决问题的关键所在,也使教师在教学中的必然行为．

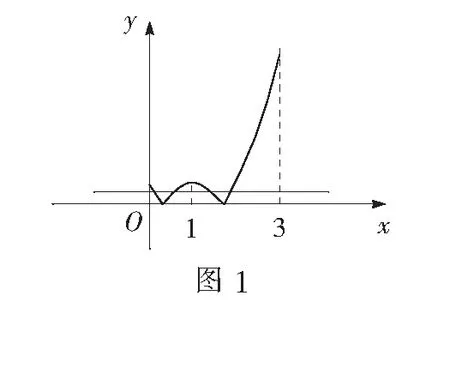
解析解决这道试题的关键是根据函数的性质画出函数当的图象.

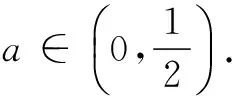
二、分类讨论的思想

张景中院士在《什么是“教育数学”》一文中指出:面对不同的情况给出不同的化解方法,全面考虑问题,这就是分类讨论思想．分类讨论的思想就是为了解决问题,我们往往会根据问题的条件不同情况进行分类,再对每种情况分别讨论,逐步解决问题,最后进行概括和归纳,解决整个问題．分类讨论的目的是把问题难点进行分解,有利于学生解决问题．为了更好地帮助学生掌握分类讨论的思想解决问题,实际教学实践中,教师要引导学生分析问题的条件,通过条件引导学生探究解决问题的方法及思路,使学生在已有的知识的基础上解决问题,使学生做到有“法”可依,有“规”可寻．例如，对含参数的不等式及含绝对值的不等式,往往需要根据题目中的给出的条件,解决问题时将其在不同条件下分别加以讨论、解决,充分地体现了分类讨论的思想．

例2设a为实数,函数f(x)=2x2+(x-a)|x-a|.

(1)若f(0)≥1,求a的取值范围;

(2)求f(x)的最小值;

解析本小题所给题目中既含有参数又含有绝对值,解决问题的主要思路是依据函数的性质、图象及解一元二次不等式等基础知识,灵活运用数形结合、分类讨论的思想方法解决问题．

(1)由f(0)=-a|a|≥1，得

(2)当x≥a时,f(x)=3x2-2ax+a2,

当x≤a时,f(x)=x2+2ax-a2,

三、转化、化归的思想

涂荣豹、王光明、宁连华在《新编数学教学论》中认为：化归思想是中学数学四个最基本且最重要的数学思想之一．在处理不等式的问题时我们经常遇到无理不等式、分式不等式、高次不等式、对数不等式、指数不等式的问题.应该引导学生审视不等式的结构特点,根据同解原理,把它们转化为已学过的一元一次不等式、一元二次不等式，并运用基本不等式的常用方法进行解题,这正是化归思想所在．实践表明,在高考中超过百分之八十的试题都与我们平时解决的问题相似或相仿.所以,在平时教学中,教师一定要抓牢学生的基础知识,引导学生审视问题的结构特点,然后制定解决问题的转化方法,培养其转化、化归的意识．在解题过程中,重要的思想就是引导学生依据条件分析是否与我们已学过的知识相关联,进一步寻求解决问题的方法与步骤．

例3已知函数f(x)=4x-2x,实数s,t满足f(s)+f(t)=0,设a=2s+2t,b=2s+t.

(1)当函数f(x)的定义域为[-1,1]时,求f(x)的值域;

(2)求函数关系式b=g(a),并求函数g(a)的定义域.

(2)由实数s,t满足f(s)+f(t)=0,得

4s-2s+4t-2t=0,

即 (2s+2t)2-2×2s+t-(2s+2t)=0.

由a=2s+2t,b=2s+t,得

a2-2b-a=0,

故a≤2,当且仅当s=t时取得等号.

综上，1

四、函数与方程的思想

《普通高中数学课程标准》指出，使学生感受运用函数概念建立模型的过程和方法,体会函数在数学和其他学科中的重要性,初步学会运用函数思想理解和处理现实生活中的简单问题．由此看来,函数与方程的思想是高中数学教学的重要思想之一．虽然函数与方程是两个不同的概念,但是我们利用函数解决问题时往往考虑函数的图象与坐标轴的交点情况,即函数的零点问题．实践表明,在解决问题时,函数与方程的思想在解决不等式的相关问题中往往发挥了重要作用．因此,在解决不等式问题时,需要把不等式的问题转化为函数问题,利用函数与方程的思想解决问题．

解析通过数学中减元的思想,把问题转化为含有一个未知量的关系式,再利用求导的方法进行解决问题．

由于y>0,所以有x>1.