暴露思维过程 提升解题能力

张 锋

(江苏省海安高级中学，226600)



暴露思维过程 提升解题能力

张 锋

(江苏省海安高级中学，226600)

解题教学不能仅仅讲解参考答案,要从学生的角度思考问题;要通过学生的自主探究、合作交流、踊跃展示来暴露思维,达到提升学生分析问题、解决问题能力的目的.

在一次县教研室举行的高三数学组备课活动中,笔者有机会听取了一节题为“解析几何与向量联袂”的观摩课,现就其中的一道例题谈谈自己的想法.

学生进行了一些思考,并在草稿纸上作了一些演算.

师:解决这道问题我们应该先设什么?(没有学生应答)

师:根据题干中向量的条件,我们选择先设出各点的坐标.

师(板书):设A(x1,y1),B(x2,y2),Q(x0,y0).

学生们窃窃私语,隐约听到的是“不会吧?”“这么多的参数怎么消?”“谁敢这样设啊?”之类的疑问.显然此时学生思考的重点不在于这道题接下来将怎么做,而是为什么这样设.

师:接下来我们将等式重新整理.(没有得到学生认同,教师继续往下讲)

师(板书):即

这时少数学生有了思路,踊跃发言.

生1:由① 式与③ 式可以解出x1和x2,② 式与④ 式解出y1和y2,代入所在圆的方程,就可以消去参数x1、x2与y1、y2了,应该就能求出点Q所在的直线方程.

师(略显尴尬):想法很好,可以算出

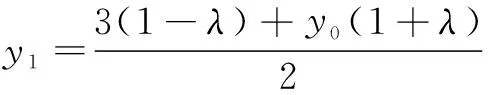
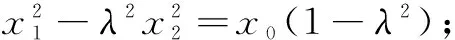
师(点头、板书):

⑤

⑥

因为点A(x1,y1),B(x2,y2)在圆x2+y2=3上,

⑤+⑥，得3-3λ2=(x0+3y0)(1-λ2).

又因为λ≠±1,所以x0+3y0=3，

故点Q总在定直线x+3y=3上运动.

听课教师发出了赞许声,上课教师长舒口气,作了些关于题干中出现向量与设点之间关系的小结,接着讲下一道例题.笔者认为这是听课教师对学生的赞许,课堂对这道例题的处理是不够充分的.从学生的反应来看,虽然他们已在教师的引导下,逐步实现对问题的解决，但他们更多地是在感叹解题方法的精巧,而不是在感知解题思路的由来，甚至可以说,这样的方法并不是他们能很快接受并在以后的学习中灵活运用的.其实，可以顺着学生思路得到如下的方法2：

虽然平方相加整理相对复杂,但利用式子的结构特征可以使得整理方向明确,较繁琐但难度不大.在解题过程中,不难发现点Q运动的根源是直线l在绕着点P旋转,故根源是直线l的斜率,于是得到下面的方法3.

当直线l斜率存在时,设斜率为k,并设A(x1,y1),B(x2,y2),Q(x0,y0).则l:y=k(x-1)+3,将直线方程代入圆方程整理得(1+k2)x2+2k(3-k)x+(3-k)2-3=0,则有

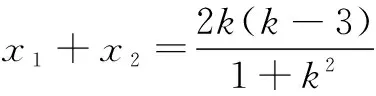
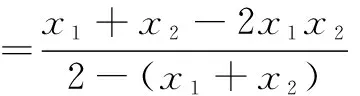
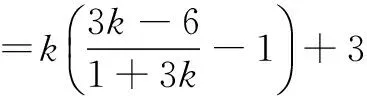
故x0+3y0=3.

综上，点Q总在定直线x+3y=3上运动.

笔者也在自己的课堂上引用了这道例题,引入斜率是学生最先提出的解题方向.虽然方法3较方法1运算量要大许多,但在较短时间里学生能抓住的本原是直线的斜率.受方法1启发,学生提出还可以从其它角度运用坐标间的关系,于是得到下面的方法4.

从以上解法不难发现,上课教师在本题的讲解过程中,主要是从例题已有的答案出发进行的引导或启发,忽视了学生已有的认知结构和题目的内在规律.上课教师先告诉学生本题应设出点的坐标,然后将式子按照答案需要进行了再加工,但学生仍未能明白教师的良苦用心,于是教师直接“启发”学生观察式子左边的结构特点,这样，教师才得到了他“满意”的答案.可以说这是一个典型的解题教学按照答案走“过场”的案例.在此过程中,学生的参与局限于顺从教师的思路,学生的思维没能得到暴露,他们提出的想法受到教师的“压制”,最终学生得到的是“精心设计、完美包装”的答案.

可见，本例题只按照参考答案讲解方法1是远远不够的,而且教师还可以将该性质类比到椭圆内.

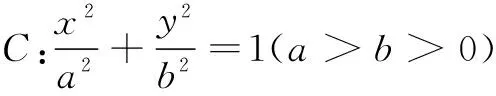
(1)求椭圆C的方程;

问题2及问题3的解决可由学生自由选择思路.学生在选择过程中就会对各种方法进行比较、筛选,不仅会利用某一方法解决问题,也对其余方法作了巩固,达到了寻求本原又优化思维的效果.如果本节课就只有问题1一道例题,让学生经历自主探究、小组讨论、踊跃展示、师生互动的教学过程,再配备问题2和问题3的巩固,是不是更能培养学生分析问题、解决问题的能力呢?

正如建构主义理论所说,知识不是通过教师传授给学生的,而是由学生依据自身已有的知识与能力主动地获得的.这就要求教师在平时的课堂教学中,从学生的角度出发,以培养学生自主分析问题、解决问题的能力为重点.学生只有在饱含自己思想的解题过程中,才能暴露思维,提高兴趣,激发灵感,提升能力.在教学过程中,教师起着引导学生进行思路探究、重组与优化的作用，千万不能按照答案走“过场”.