以生为本的课堂解题训练活动的设计

2016-12-30施培松

高中数学教与学 2016年20期

关键词：通项公差变式

施培松

(安徽省颍上第一中学，236200)

○数学教育○

以生为本的课堂解题训练活动的设计

施培松

(安徽省颍上第一中学，236200)

解题是深化知识、发展智力、提高能力的重要手段.规范的解题能够让学生养成良好的学习习惯,提高思维水平.笔者阅读过很多杂志上关于解题指导的文章,其中不乏一些解题技巧．然而也为这种追求技巧,忽视通性通法的趋势感到担忧．有的作者研究出了解决高考题的最简洁的方法,比如说数形结合判断零点个数,就有以图代证之嫌;有作者以为自己发现一个“定理”,并指出在解题中使用可以大大地降低运算量,用“定理”省略了很多该写而不写的过程,当然运算量减小了;有作者发现了教材习题的结论并应用于解题,等等．诸如此类,笔者则担心这些方法、“定理”在高考阅卷中是否给分,能给多少分?

一、从学生的认知困惑点出发,寻找问题突破口

案例1数列{an}与{bn}的通项公式分别为an=4n-1,bn=3n+2,它们的公共项由小到大排成的数列是{cn},求{cn}的通项公式.

生1:{an}与{bn}的公共项由an=bn求得,即4n-1=3n+2,只有一项．

对于上述学生1的求解方法,首先应该肯定学生对数列的公共项的理解；但又对公共项缺少具体感知,导致找不到问题解决的突破口,心里明白但无从下手．因此,评讲开始应该启发引导学生完成对公共项的特征的感知与探索．

生2:列举出两数列的前几项:

{an}:3,7,11,15,19,23,27,31,35,39,43,47,51,55,59,…

{bn}:5,8,11,14,17,20,23,26,29,32,35,38,41,44,47,…

发现两个数列的公共项是11,23,35,47,…,不难看出该数列是首项为11、公差为12的等差数列,则cn=11+12(n-1)=12n-1．

当学生对两个等差数列的公共项的周期性呈现有了一定的感知之后,可能还会产生一点误解或者困惑.较典型的是从函数的角度看一次函数的交点本来应该是一个,怎么会出现这么多的公共项?其实这也是很好的可以利用的教学资源.学生认为关于n的一次方程an=bn只有一个解本身是对的,但是学生对公共项的对应关系感知不够,没有注意到公共项在格子数列中的位置因公差的大小而不同,从而得出cn=am=bk这个关键的条件,推动思维的进一步迁移．

二、从学生已有的知识经验现状出发,展开解题思路的探究

学,是在教之下的学;教,是为学而教．教学过程是一种特殊的认识过程,这种认识是在教师有目的、有组织、有计划的引导下,学生主动地接受间接经验和知识,主动探索生成新的认知的师生共同活动的过程.

对于案例1,大部分学生可能会在教师的启发引导下,顺利地感知到了公共项的特征,甚至能够成功地获得通项公式.通常情况下学生肯定会就此结束解题活动,教师就应该站在学生拿满分的角度,从学生们已经能够意识到“说明一个数列是等差数列需要根据定义严格推理论证”的基础出发,引导规范答题．这样，也就很自然地把探究活动引向“证明(此时的)公共项是等差数列” 的思路上来．

设an=bm=ck,则ck=4n-1=3m+2.

∴an+1=4(n+1)-1=3m+2+4=3(m+2)∉{bn},

an+2=4(n+2)-1=3m+2+8=3(m+3)+1∉{bn};

an+3=4(n+3)-1=3m+2+12=3(m+4)+2∈{bn},

∴ck+1=an+3,∴ck+1-ck=an+3-an=12,

∴{cn}构成公差为12的等差数列.

又∵c1=a3=11,

∴cn=11+12(n-1)=12n-1.

如何证明一个数列是等差数列，学生是知道利用定义去证明的.但是一般习题都有已知条件,比如告诉通项公式或相邻两项的ck,ck+1递推关系,而本题是没有的,那么寻找ck,ck+1成为当前首要任务．学生知道ck,ck+1肯定是两个数列中的相邻的两个公共项,因此寻找ck,ck+1就变成了在数列{bn}或者在数列{an}中寻找相同的项的思维活动.不难发现:若bn=2n+7就是ck,依次检验bn+1、bn+2、bn+3，到这一步,如何判断bn+3属于{an}成为整个活动的思维难点．

因为我们已经假设了2n+7就是第k个公共项ck,那么我们同样也看不出它是属于{an}的,这是事实；但是ck=bn,而ck=am也是事实,学生都是知道的．可见把数列{bn}中的项化成数列{an}中的项,必然需要bn=am这个隐含条件的协助．

三、从学生理解能力的发展变化出发,循序渐进领悟问题本质

当前不少变式教学,没有遵循循序渐进规律,有的变式是在教师刚刚教会一种方法,在学生还没对解题方法的本质有较高的认识的时候,一连串的变式就把学生的思维带到“天上”.总认为“变式”就是拓展,就是知识交汇,步子迈得太大,脱离了学生的理解能力发展水平．

对于本节课的引例的解题思路探究,学生也许能够会做类似问题,但可能并不熟练,因此需要循序渐进地螺旋式提高解题能力．笔者认为,在最初阶段我们应该安排一定量的变式与巩固训练,在训练中巩固和规范解题思路,才能进一步理解某些关键步骤,亲身体验过程操作技巧.

案例2数列{an}与{bn}的通项公式分别为an=2n,bn=3n+2,它们的公共项由小到大排成的数列是{cn},求{cn}的通项公式.

解析设an=bm=ck,则

ck=2n=3m+2.

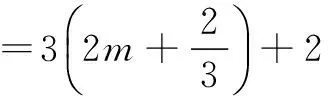
an+2=4·2n=4(3m+2)

=3(4m+2)+2=b4m+2∈{bn},

∴ck+1=an+2,也就是当ck=an时必有ck+1=an+2.

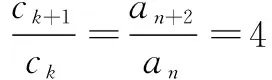
∴{cn}构成公比为4的等比数列.

∵c1=a3=8,∴cn=22n+1.

案例2将案例1中的一个等差数列变为等比数列,由于等比数列{an}的项变化要比等差数列快,数列中的相邻的公共项之间距离只间隔一项,即ck=am,ck+1=am+2,而等差数列中的相邻的公共项之间的距离就相当远,假如bn=ck是第k个公共项,那么下一个公共项是b4m+2=ck+1,再次验证了两个等差数列公共项,应该尽量在公差较大的数列中找ck与ck+1之间的关系．

四、在多背景变化中突破思维定势

在初步认识并形成了对数列的公共项的较稳固的思维模式之后,就可以变换不同视角,放手让思维活跃的学生展示不同想法,并通过与已有的解题思想进行比较,体会各自的优点和不足,在比较中让更多的学生尤其此类学生,感悟通性通法的魅力．当学生认识到此类问题的通法之后,笔者在下一课时又安排了新背景的变式试题．

案例3已知数列{an}和{bn}的通项公式分别为an=3n+6,bn=2n+7(n∈N*).它们的公共项由小到大排成的数列是{cn}．求数列{cn}的通项公式．

背景1数列是研究数字的,数集也是研究数的,除了有序性、可重复性以及表示形式不一样外,并无别的差别．所以,我们最先想到数列问题是可以以集合作为背景的．

(1)已知数列{an}和{bn}的通项公式分别为an=3n+6,bn=2n+7(n∈N*).将集合{x|x=an,n∈N*}∩{x|x=bn,n∈N*}中的元素从小到大依次排列,构成数列c1,c2,c3,…,cn,…,求数列{cn}的通项公式.

(2)若集合{x|x=3n+6,n∈N*}∩{x|x=2n+7,n∈N*}中的元素从小到大依次排列,构成数列c1,c2,c3,…,cn,…,求数列{cn}的通项公式.

(3)若集合A={x|x=3n+6,n∈N*},B={x|x=2n+7,n∈N*}.若等差数列{cn}任一项cn∈A∩B,c1是A∩B中的最小数,且109

以上问题其实就是前面研究的数列公共项问题,过程从略．

背景2我们知道,两个数列所在的集合的交集就是公共项的集合,那么有没有可能研究两个数列所在的集合的并集,这样可以考查集合的互异性,间接考查数列的公共项．

(1)已知数列{an}和{bn}的通项公式分别为an=3n+6,bn=2n+7(n∈N*).将集合{x|x=an,n∈N*}∪{x|x=bn,n∈N*}中的元素从小到大依次排列,构成数列c1,c2,c3,…,cn,….

证明在数列{cn}中,但不在数列{bn}中的项只有a2,a4,…,a2n,…．

解析由题意,即证a2n∉{bn},且a2n-1∈{bn}.

① 任意n∈N*,设a2n-1=3(2n-1)+6=6n+3=2(3n-2)+7=b3n-2,则a2n-1=b3n-2;

上述问题是借用了寻找公共项的方法,是属于一种方式的变用,内涵较为隐蔽．

(2)已知数列{an}和{bn}的通项公式分别为an=3n+6,bn=2n+7(n∈N*).将集合{x|x=an,n∈N*}∪{x|x=bn,n∈N*}中的元素从小到大依次排列,构成数列c1,c2,c3,…,cn,…,求数列{cn}的通项公式.

解析由前知得公共项dk=6k+3,dk+1=6k+9,相邻两个公共项之间,还有数列中{an}和{bn}的非公共项．由于a2k=6k+6,a2k-1=6k+3,b3k=6k+7,b3k-1=6k+5,b3k-2=6k+3,也就是说并集中的元素被分成四类,从小到大顺序排列为:6k+3,6k+5,6k+6,6k+7．

所以当k=1时,依次有

当k=2时,依次有

……

上述解法是先确定数列{an}和{bn}的公共项dk与dk+1,再寻找dk与dk+1之间元素存在的规律.

(3)数列{an}与{bn}的通项公式分别为an=4n-1,bn=3n+2(n∈N*).将集合{x|x=an,n∈N*}∪{x|x=bn,n∈N*}中的元素从小到大依次排列,构成数列c1,c2,c3,…,cn,…,求数列{cn}的通项公式.

解析由前面的推导方式得公共项dn=12n-1,dn+1=12n+11,相邻两个公共项之间,还有数列中{an}和{bn}的非公共项．

由于a3k=12k-1,a3k+1=12k+3,a3k+2=12k+11,b4k=12k+2,b4k+1=12k+5,b4k+2=12k+8,b4k+3=12k+11,也就是说并集中的元素被分成五类,从小到大顺序排列为:12k-1,12k+2,12k+3,12k+5,12k+8．

所以,数列{cn}的通项公式