迎浪工况下气垫船运动响应研究*

刘 宁 刘晓媛

(哈尔滨工程大学船舶工程学院 哈尔滨 150001)

迎浪工况下气垫船运动响应研究*

刘 宁 刘晓媛

(哈尔滨工程大学船舶工程学院 哈尔滨 150001)

对全垫升气垫船在迎浪工况下的运动响应进行了分析研究，介绍了气垫船在波浪中的时域线性运动响应和时域非线性运动响应，并采取龙格-库塔数值模拟方法，运用Fortran语言编程求解了在不同波浪频率、迎浪工况下的气垫船时域线性与非线性运动响应，分析对比了两者结果得出响应结论.根据气垫船的运动响应求得了静水中和规则波下的波浪载荷.

气垫船；迎浪工况；运动响应；波浪载荷

对气垫船的研究起于20世纪上半叶，发展至今已经有近80年的历史.从Reynolds等[1]推导出全垫升气垫船的线性运动方程，到Doctors等[2-3]在雷诺兹等人研究的基础上，将运动理论从频域发展到时域，准确列出气垫船在波浪中运动时的非线性运动微分方程，气垫船的运动响应求解经历了漫长的过程[4-6].文中使用Fortran程序求解了某全垫升气垫船在波浪中的时域中的线性运动响应和非线性运动响应，并且根据气垫船的运动响应求得了静水中和规则波下的波浪载荷.

1 气垫船在波浪中的运动响应

气垫船在波浪中的运动响应求解是求解气垫船结构设计载荷的前提工作，也是研究解决气垫船结安全性的关键问题，同时也是气垫船研究中的难点问题.通过合理的假设，列出假设下的运动响应方程组，最后求解该方程组就是解决问题的主要思路.文中求解了气垫船的时域下的线性运动响应和非线性运动响应，并给出了相应的结论.

1.1 气垫船的线性运动响应

1.1.1 基本假设

(1) 承认傅劳德-克雷洛夫假设，认为船的存在不影响波浪中压力的分布和波浪的形状；(2) 认为气垫压力(前、后)均匀分布；(3) 将气垫面积(前、后)近似简化为矩形；(4) 认为气垫内空气密度及压力变化过程满足热力学绝热压缩定律；(5) 忽略围裙触水产生的水动力影响；(6) 忽略风扇动态响应影响.

1.1.2 平衡状态计算

二气室全垫升气垫船在静垫升状态时的垂向力平衡方程和各个力对重心的力矩之和为0的平衡方程可写为

式中：Ac1，Ac2为前后气垫面积；pc1，pc2为前后气室的气垫压力；xp1，xp2为前后气室压力中心纵向坐标；W为船体的重量；M0为船所受到的阻力和推力所引起的对船重心的力矩.

1.1.3 风扇风道特性方程

风扇风道特性方程可写为

Hf=Af+BfQ-CfQ2

前后气室的气垫压力分别为下式

式中：Hf为风扇总压；Q为风扇流量；Af，Bf，Cf为风扇的有因次系数。

假设全船只有一个风扇，且风扇的出口直通围裙囊，且围裙囊直通全船，空气气流经过围裙囊的囊孔后直接流入到气垫.

令

式中：K为风道损失系数；ρa为空气密度；AFK为风道特征面积；Cj为囊孔收缩系数；Aj为囊孔面积。

1.1.4 波浪方程

1.1.5 流量连续性方程

前、后气垫的逸流量由2部分组成:(1)气垫向大气的逸流流量;(2)前、后气垫之间的逸流流量.

1.1.6 结果求解

联立以上方程组，使用龙格库塔数值模拟方法求解出气垫船时域中的线性运动响应，见图1～4.图1、图3中纵坐标为升沉运动幅值的无因次量；图2、图4中纵坐标为纵摇角度的无因次量，横坐标均为运动周期.

图1 w=0.4时的升沉运动变化规律

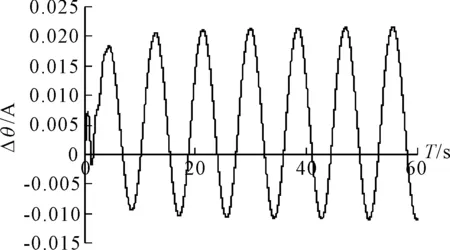
图2 w=0.4时的纵摇运动变化规律

图3 w=2.0时的升沉运动变化规律

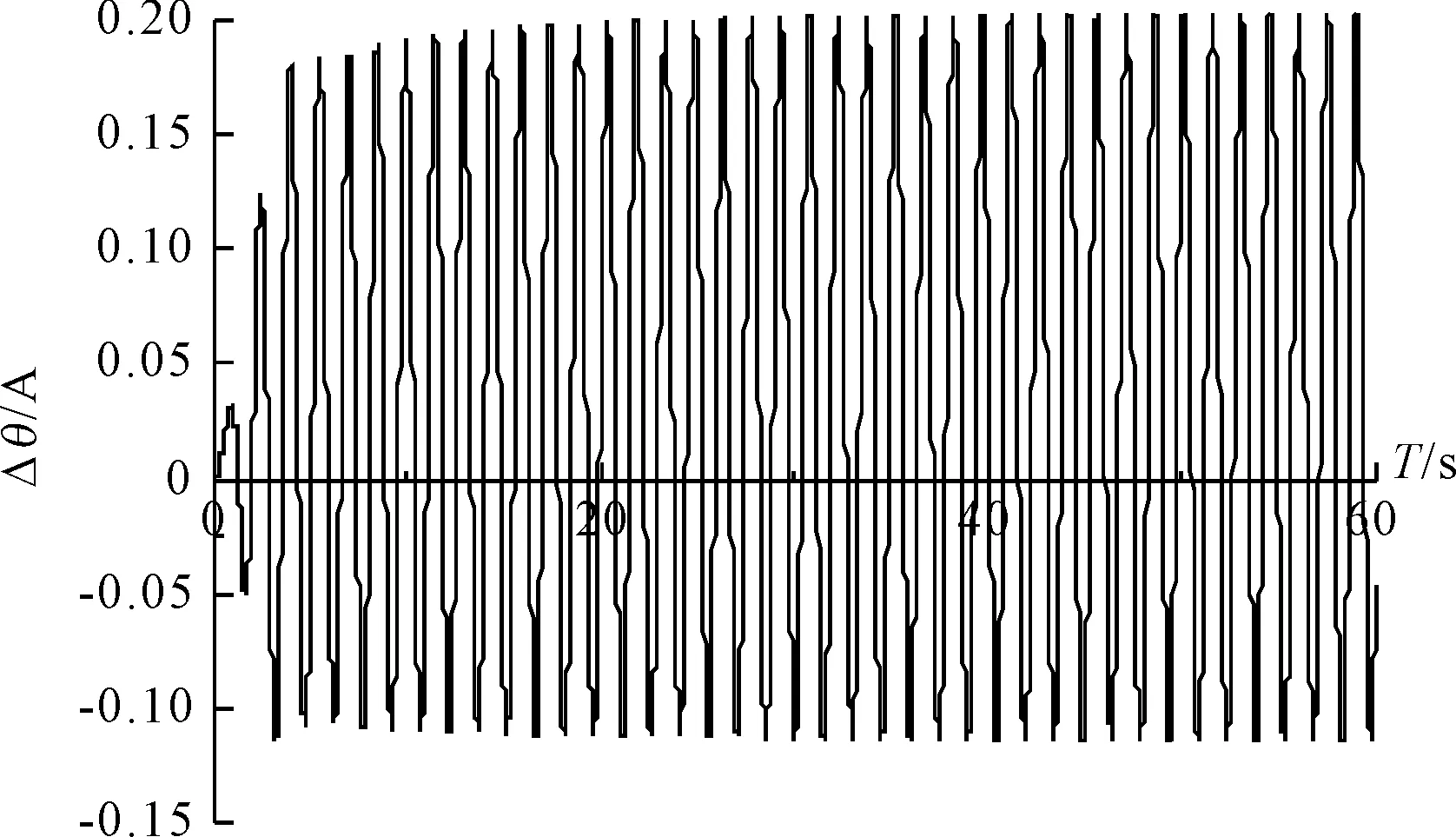
图4 w=2.0时的纵摇运动变化规律

由图1～4可知：

1) 气垫船的升沉和纵摇运动响应频率均随着波浪频率的加快而加快，但是运动响应的幅度却不是单调变化的，而是有增有减.

2) 当波浪频率较低时，气垫船从接收波浪扰动直到运动响应的稳定需要较长的时间，w=0.4时，气垫船的运动响应达到稳定的过程经过了20 s，w=1.2时，经过10 s基本到达稳定状态.

3) 随着波浪频率的增加，气垫船的运动响应逐渐发生周期性震荡.

4) 从图像中可以看出气垫船的升沉运动响应是纵摇运动的数倍，在高频波浪下，升沉响应的幅度甚至达到了纵摇响应幅度的近20倍，由此可以推测这是由于在高频波浪下，气垫船气室下的波浪分布得细密，因此纵摇响应幅度不大.

5) 气垫船在某一频率下的升沉运动响应和纵摇运动响应之间存在着约90°的相位差.

1.2 气垫船的非线性运动响应

时域非线性运动响应是在线性运动的基础上求解的，线性假设中认为气垫船围裙不触水，但实际情况是围裙触水时气垫船受到力作用，文中使用平板砰击力代替，砰击压力公式为

求解结果见图5～8.

图5 w=0.2时的升沉运动变化规律

图6 w=0.2时的纵摇运动变化规律

图7 w=1.0时的升沉运动变化规律

图8 w=1.0时的纵摇运动变化规律

由图5～8可知：

1) 气垫船运动响应频率随着波浪频率的增加而增加.

2) 随着波浪频率的增加，气垫船运动响应达到稳定状态所需要的时间也越来越短，如图可见w=0.2时经历约20 s到达稳定状态，w=1.0时经历约12 s到达稳定状态.

3) 随着时间增加，某一波浪频率下的气垫船运动响应逐渐达到平衡状态.

4) 气垫船的升沉运动和纵摇之间存在90°的相位差.

1.3 运动响应比较

对1.2和1.3所求得的气垫船在波浪中的线性和非线性时域运动响应结果经行比较和分析，见图9～12.

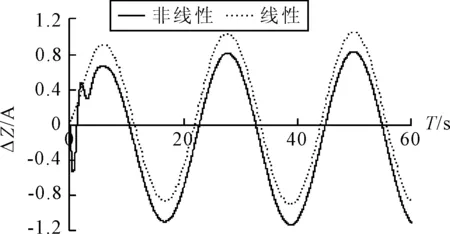
图9 w=0.2时的升沉运动变化规律对比

图10 w=0.2时的纵摇运动变化规律对比

图11 w=0.6时的升沉运动变化规律对比

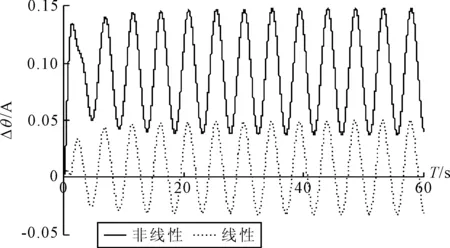
图12 w=0.6时的纵摇运动变化规律对比

根据以上几个具有代表性的运动响应，主要从线性与非线性的差别来讲，可以分析得出如下结论.

1)w=0.2时，线性与非线性升沉运动的幅值差别不大，但平衡位置存在一个较小差异，说明不加砰击项时，气垫船以静水面为平衡位置往复运动，而加入砰击时，由于受到向上的力的作用，故平衡位置在垂直向上的方向上有所移动.

2)w=0.2时，加入砰击以后的总要运动幅度变化不大，但是平衡位置也是有所抬升的，由于以抬艏为正，那么投影入实际船体的等价形式就是气垫船的抬艏高度有所增加，船呈现一个尾倾的姿态，但由于数值较小，因此不会对气垫船产生灾难性的影响.

3)w=0.6时，可知气垫船运动的频率较w=0.2时有明显的增加，线性运动响应的变化规律与w=0.2时基本类似，但可看出非线性运动的幅度较线性运动有一些减小，这是由于围裙与水面发生砰击时，使得船的运动受到阻碍，从而不能像线性运动一样达到无阻碍时的位置，因此幅值有所减小，而这种幅值减小的情况是随着波频增大而逐渐显著起来的.

4)w=0.6时，气垫船纵摇的运动响应情况与W=0.2时类似，达到稳定后作规律的往复振动，随着频率的增加，气垫船的纵倾现象更加严重了，但是数值依然是很小的.

5) 总体上来讲，加入砰击项后，气垫船的运动响应在加波浪的前期变得比线性运动更加地复杂而紊乱，需要一段时间才能达到稳定状态，稳定后能呈现规律性较强的往复振动，总体上尾倾现象变得更加严重，但数值很小，因此影响不大，升沉运动的变化随着频率的变化不是线性的.

2 气垫船波浪载荷预报

2.1 气垫船在静水中的载荷响应

2.1.1 质量分布

由于目标船仅作理论研究用，因此并没有质量分布数据，因此根据气垫船船型肥胖的特点使用梯形的质量分布进行代替，原理来自于《船舶结构强度》.

2.1.2 气垫船垫压分布

由于假设气室(前、后)压力与位置无关，因此，气垫压力分布函数可表示为

2.1.3 气垫船的静水剪力、弯矩

图13 静水剪力

图14 静水弯矩

由图13～14可知：

1) 气垫船的最大剪力发生在第8站的位置，最大剪力约为140 kN，这与常规排水型船舶的最大剪力通常发生在距离首尾1/4处的情况有所不同，产生这种现象的原因在于气垫船与常规排水型船舶的受理方式不同，常规船舶以水压力作为主要浮力，而气垫船以空气抬升，常规船受到来自水的浮力沿船长是连续变化的，而气垫船前后两个气室的压力不同，因此浮力有间断突变处，由于这些原因，会导致最大剪力发生的位置发生一定的偏移.

2) 气垫船的最大弯矩发生在30站左右，最大值约为1 200 kN·m与普通排水型船舶最大弯矩发生在船中处有一定的差别，其中主要原因还是由于两者受力上的区别，对此不再赘述，而最后弯矩的曲线没有回到零点，一方面是由于气垫船在静水中受到来自阻力和推力引起的力矩，另一方面是由于质量分布模拟与实际质量分布存在一些差异的问题.

2.2 气垫船在规则波中的载荷响应

以第8站为例，计算了第8站剖面处的剪力和弯矩的幅值的无因次量，分别以波长无因次量和波频无因次量为自变量的变化规律，见图15～18.纵坐标为剪力与弯矩幅值的无因次量，横坐标为无因次数值与无因次频率.

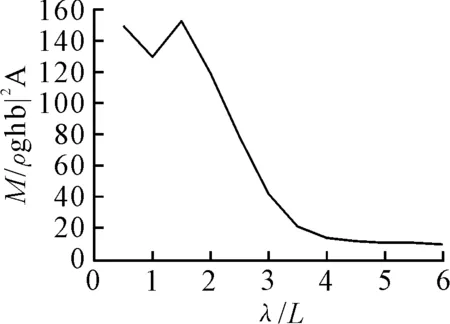
图15 弯矩随无因次波长变化规律

图16 剪力随无因次波长变化规律

图17 弯矩随无因次遭遇频率变化规律

图18 剪力随无因次遭遇频率变化规律

由图15～18可知：

1) 弯矩的极大值出现在波长船长比在1～2附近，大小为150，说明当波浪长度在此范围时，第8站剖面弯矩达到最危险的状态，同时可以看出在此处附近剪力也同时达到最大值6.0，因此可以得出结论对于此剖面来说，波长船长比为1～2时的情况下是需要校核强度的.

2) 第8站处弯矩随无因次遭遇频率的变化规律不是单调的，分别在无因次遭遇频率为8和20时都达到最大值150，并且剪力在频率为8附近达到最大值6，因此无因次频率为8和20时都需要进行校核.

3 结 束 语

气垫船的线性运动响应和非线性运动响应的区别在于，非线性运动响应是在线性方程的基础之上加入了砰击效应的影响，即考虑围裙触水的情况，并用平板砰击理论计算围裙触水时所受到的外力，更加真实地模拟出现实情况，并使用Fortran编程，这一过程的核心难点在于如何确定砰击加载的条件，解决方法是判定砰击发生前后时刻气垫船围裙与波浪之间的相对位移大小，文中认为只在前一时刻相对位移大于零，而后一时刻相对位移不大于零的情况下才发生一次砰击，其余情况下无砰击.

通过已经求得的气垫船时域运动响应对气垫船波浪载荷预报，使用梯形质量分布来模拟气垫船的质量分布情况，使用梯形法求解定积分算出气垫船在静水中的各剖面剪力弯矩图，在波浪载荷预报中，根据达朗贝尔原理对气垫船进行受力分析，计算气垫船在波浪中所受剪力弯矩情况.

下一步的研究工作：(1)文中在求解气垫船在波浪中的运动响应时假设前后气室的垫压均为某一数值，在该气室中不随位置发生变化，这与实际情况是有出入的，因此有必要运用流体力学相关知识对气垫中的流场进行更加符合真实情况的数值模拟；(2)文中假设气垫船围裙为刚体，受力时并不发生形变而产生内力，这与实际情况也是不符的，因此对于气垫船围裙的柔性及其形变受力等情况应该有更加深入的研究；(3)文中假设忽略水动力对气垫船产生影响，但实际情况是围裙或者船体入水时是会受到水动力的，水会对气垫船在水中的运动产生一定程度的阻力，这一方面也是未来工作的一项研究内容.

[1]REYNOLDS A J, WEST R P, BROOKS B E. Heaving and pitching response of a hovercraft moving over regular waves[J]. Journal of Mechanical Engineering Science,1972,14(5):89-95.

[2]DOCTORS L J.Nonlinear motion of air cushion vehicle over waves[J]. Journal of Hydronautics,1975(1)：55-58.

[3]KAPLAN P, SCHNEIDER J, GOODMAN T R. Motions of air cushion vehicles in waves[J].Symposium on the Dynamics of Marine Vehicles and Structures in Waves,1974(2):75-80.

[4]周佳，唐文勇，张圣坤.全垫升ACV全圆周浪向下耐波性分析[J]. 中国造船,2009，50(2)：100-108.

[5]周佳，唐文勇，张圣坤. ACV三维耐波性分析[J]. 船舶力学，2009，13(4):256-261.

[6]周佳，唐文勇，张圣坤.全垫升ACV耐波性参数敏感度分析[J].上海交通大学学报,2009，43(10):555-560.

Research on the Motion Response of Air Cushion Vessel in the Condition of Head Sea

LIU Ning LIU Xiaoyuan

(CollegeofShipbuildingEngineering,HarbinEngineeringUniversity,Harbin, 150001,China)

The motion responses of the hovercraft in the condition of head sea are analyzed in this paper. The time-domain linear motion response and time domain nonlinear motion response of the hovercraft are introduced, respectively. Based on the Runge-Kutta numerical integration method, FORTRAN language is used to solve the time-domain linear and nonlinear motion response under different wave frequency and head sea. The results of the two methods are analyzed and compared, and the wave loads are obtained according to the motion response of the air cushion ship.

air cushion vessel; head sea; motion response; wave load

2016-10-31

*国家留学基金青年骨干项目(201606685032)

U674.34

10.3963/j.issn.2095-3844.2016.06.008

刘宁(1981—)：男，博士，主要研究领域为环境载荷和结构强度