基于改进BP神经网络的驼峰场车辆减速器故障诊断的研究

姜雪杰，李国宁

(兰州交通大学自动化与电气工程学院，兰州 730070 )



基于改进BP神经网络的驼峰场车辆减速器故障诊断的研究

姜雪杰，李国宁

(兰州交通大学自动化与电气工程学院，兰州 730070 )

减速器是驼峰场控制速度的主要部分，随着当前高速铁路大发展和铁路货运量的提高，编组站解体和编组能力加大，车辆减速器使用率和故障率增加，而现场维修人员凭借经验的低效率维修已经不能满足当前的货运溜放要求，对驼峰溜放控制，钩车安全连挂提出更高的要求，因此根据现场收集的数据建立BP神经网络模型进行仿真训练，精确诊断驼峰车辆减速器T•JK(Y)2，3的故障部位，仿真结果表明，故障判断准确率达到96%。

驼峰；T•JK(Y)车辆减速器；BP神经网络；故障诊断

目前网络购物量增加，铁路货运仍然是当前最主要的货物运输方式之一，编组站驼峰场解体编组压力增大，减速器故障发生率显著提高，而现场维修人员不能及时发现并处理故障，严重影响作业效率，而且有可能会由于操作不当危及维修人员人身安全，所以研究驼峰车辆减速器的故障诊断具有重要意义。文献[1]中提出了使用涡流制动技术来替代原有的机械制动新方法，有效地减少碰撞摩擦，改善了现场的噪声环境，但现场还没有实际应用。

1 T•JK(Y)减速器原理

1.1 T•JK(Y)减速器机构原理

当前我国铁路编组站现场主要使用的是T•JK(Y)2，3型车辆减速器[2]，因此本文首先介绍这种类型的减速器原理。减速器机构如图1所示。

从图1可以看出，减速器的制动部分和传动部分均是平面运动机构。减速器的制动部分由5个部件组合而成，其中4个活动部件(1、2、3、6)和1个固定部件。部件1、3与部件6铰接于O1和O2，形成2个转动副；部件1、3尾部置于滚轮n1和n2上，形成2个平面高副；部件2和部件6之间形成一个移动副，和固定部件之间形成另一移动副。减速器的制动部分为2个自由度的平面机构。这些机构对驼峰车辆减速器的正常工作是极其重要的。即制动钳可绕O1和O2转动，使减速器制动和缓解，同时制动钳还可以左右移动，以适应车辆的蛇形运动。

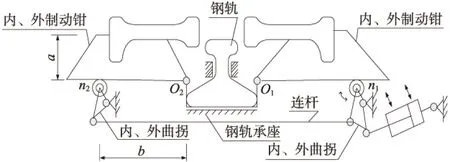
图1 T•JK(Y)型减速器机构原理

1.2 T•JK(Y)型减速器制动力分析

由于T•JK(Y)型减速器是浮轨重力式减速器，因此，减速器制动轨对车轮的侧压力P除由车重和减速器的杠杆比所决定以外，而且和浮动基本轨变形所产生的附加力，以及在减速器入口和出口段车轮重力的传递有关。本文把驼峰车辆减速器的机械杠杆比和被减速器制动车辆的轴重分别设为K和Q轴，由于浮动基本轨变形产生的附加侧压力为F1，进出口车轮重量传递所产生的附加侧压力为F2，所以制动轨板对被制动车辆的车轮产生的侧压力

式中K——车辆减速器的机械杠杆比，由减速器结构所决定；T•JK(Y)型减速器的杠杆比如图1所示，K=b/a；

F轴——浮动基本轨变形所产生的附加侧压力F1和进出口车轮重力传递所产生的附加侧压力F2的总和。

通过分析驼峰车辆减速器的机械原理，当前铁路部分采用27 t轴重C80车辆对减速器造成更多的疲劳损伤，而且有些损害具有隐蔽性，因此迫切需要使用智能故障诊断对现场人工不能及时处理的故障进行监督管理和智能诊断。

2 改进BP神经网络模型

收集现场车辆减速器故障的数据进行归纳分类和分析[3-5]，从编组站综合自动化系统中可以得到测重、测速、测距、制动缓解表示、气压值、工作温度、电流、电压、电阻、熔断器、动作时间等需要的数据，这些数据都由现场的传感器等设备来获得，还有振动频率，紧固状态，开口尺寸等变量，本文采用安装陀螺仪和视频来进行监控，然后进行信号处理，由于本文采用公式(2)的S型函数，所以还需要对数据进行归一化处理，以达到故障诊断的目的。BP神经网络的输出为图2分析的主要故障部分。

本文隐含层和输出层传递函数采用Sigmoid型函数

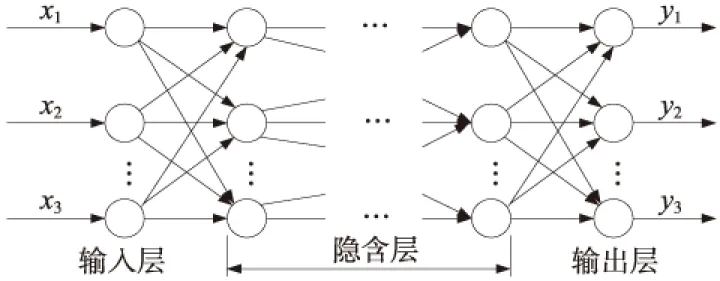
图2 神经网络模型

网络的输入用向量X来表示，输出用向量Y来表示，即

给定样本集合

BP网络的权值将进行调整，以使式(7)的误差目标函数达到最小

式中，N为样本数；K为神经网络输出量个数；Cim为BP网络的输出量；Yim为期望的输出量。

为了提高网络的泛化能力，采用基于贝叶斯正规化算法与LM(Levenberg-Marquardt)算法相结合的方法[6]。

使用正规化方法将网络性能函数改进为

其中，EW为网络权重平方和

式中，Wi为网络的权值；ED为误差函数；l、q控制着其他参数(权及阈值)的分布形式，称其为超参数

式中，常数n为网络中参数的数量个数；变量H为性能函数海森(Hessian)矩阵；α为动量因子。

超参数的大小决定着神经网络的训练目标，如果l≪q，则训练算法把大量减小训练误差作为主要的目的；如果l≫q，则训练算法是为使网络产生更为平滑的响应作为主要目的。因此，改进应该在尽可能减少有效的网络参数，弥补较大的网络误差上面作出改进。

本文所采用的正规化算法通过采用新的改进网络性能指标函数，在保证网络训练误差大大减小的情况下，并且使网络中的有效权值尽量减少，从而在本质上等于自己调整，结果缩小了网络的规模。然而常规的正规化方法难以确定公式中的超参数l、q的大小，而本文的贝叶斯正规化方法，其可以在网络训练的过程中自动地调整超参数合适的大小，从而使其达到最优的结果。

本文使用了贝叶斯正规化算法和LM算法的结合，由于LM算法的精确性较高还不用计算海森(Hessian)矩阵，既包含有牛顿法的局部收敛特性，又包含有梯度下降法的全局收敛特性；而且贝叶斯正规化算法还可以提高网络的泛化能力，因此提出采用两者结合的方法来实现驼峰车辆减速器的故障诊断。具体步骤如下：

(1)先把网络初始化，然后计算出网络隐含层的输出量和输出节点的输出量，误差以及误差平方和函数，本网络令r=n；

(2)计算本文的超参数l与q以及误差性能函数，如果达到目标误差则停止计算，否则继续；

(3)在前面算法的基础上进一步使用LM算法，使性能函数的迭代进一步减小；

(4)再计算新的r、l、q和网络性能函数，如果最大逼近目标误差或达到了最大训练次数则停止，否则转(3)重复计算。

式中，η为常数量，用来表示学习的步长(在变步长算法中η可以调整)；其中变量G(k)为E(W)的负梯度，即

为了使BP算法有更快的收敛速度，引入了动量因子α来改善迭代，从而将式(10)的权向量迭代的修正规则改为

式中

式(13)记忆了上一时刻的权向量修正的方向，从而使式(12)的形式与共轭梯度算法相似。动量因子α的取值范围是0< α<1，动量因子大小的选取对网络学习的收敛速度有着非常重要的调整作用。

因此采用改进的BP神经网络，由于其收敛速度快、泛化能力强的优点，特别适用于对驼峰车辆减速器进行故障诊断研究。

3 改进BP神经网络对驼峰车辆减速器的故障诊断(图3)

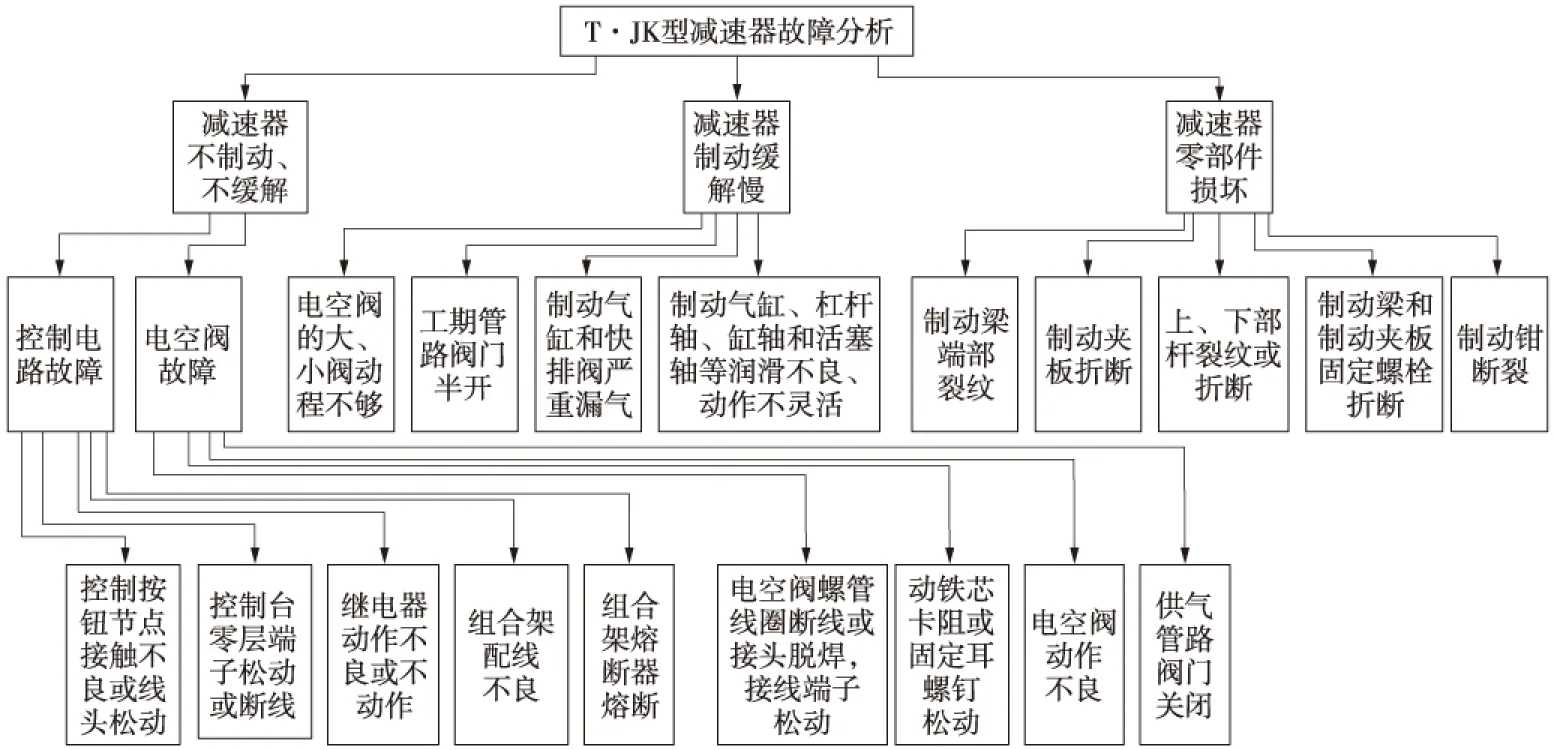
图3 T•JK(Y)型减速器故障分析

3.1 输入量的确定

将上述改进的BP神经网络[7]用于驼峰车辆减速器故障诊断，通过文献[8，9]分析研究影响T•JK(Y)型减速器的主要元素为测重、测速、气压值、控制电路电流、电压、制动夹板开口尺寸、动作时间、车轮厚度、振动频率。因此将上述主要部分元素作为改进BP神经网络的输入变量，因此确定输入节点的个数为9个。为了更好地采用收集数据的有效信息，首先对数据进行粗大误差处理，从而去掉明显影响网络收敛精度的不可靠输入数据，还要进行归一化处理，以利于网络的学习训练。

3.2 输出量和隐含层节点数的确定

由图3选择减速器经常故障的电空阀故障、控制按钮节点接触不良、制动夹板断裂、上下部杆断裂、制动钳断裂、继电器故障等6个故障作为网络的输出，因此网络的输出数为6个。

如何选取BP网络的隐含层数，以及隐含层的节点数，目前尚无准确的理论和方法对其进行确定，而需要针对特定的问题对象，反复多次试验研究后来确定。目前有3种确定三层BP神经网络的隐含层节点数h的经验参考公式

其中，n为输入神经元数；m为输出神经元数；z为1～10之间的常数。

通过改变隐含层的节点数来比较其网络收敛的性能，然后根据网络的性能来确定最合适的隐含层节点个数。根据收集到的100种故障类型，取90种故障数据进行网络训练，10种故障数据进行网络测试，训练次数设置为1000次，对比不同隐含层结点个数情况下网络的均方误差(Mean Square Error，MSE)，如表1所示。从表1可以看出，当隐含层节点数为13的时候，训练样本和测试样本MSE最小，因此本文的改进BP神经网络最合适的隐含层节点数选择为13个。

表1 不同网络结构下神经网络MSE比较

3.3 T•JK(Y)型减速器故障诊断结果及分析

由上文确定改进BP神经网络输入输出以及隐层节点数，然后在输入同样的车辆减速器故障[10-13]的训练样本，图4为贝叶斯正规化的BP神经网络故障结构流程图，而且网络最大训练次数都设置为1 500步，最小误差都设置为10-3，分别用BP神经网络和本文提出的改进BP神经网络对其进行训练，取得最好的一次训练结果，由Matlab编程可得比较的训练误差仿真曲线如图5所示。

图4 贝叶斯正规化的BP神经网络结构框图

图5 传统和改进BP神经网络误差比

由图5可知，BP神经网络和改进BP神经网络在减速器故障诊断中的平均误差、收敛时间及收敛精度等方面有显著的差异。BP神经网络在经过1180步运算达到预设的精度，显然其收敛时间长，因为BP神经网络虽然具有非线性映射的能力，但是其很容易陷入局部极小值，因此不能满足减速器故障诊断的实时性。而使用本文改进的BP神经网络经过857步运算达到预设收敛精度，其收敛速度明显较快，并且能很好地解决局部收敛问题，能够满足驼峰车辆减速器故障诊断的要求。

训练完成后，将训练好的改进BP神经网络用于对T•JK(Y)型车辆减速器进行故障诊断，测试样本的诊断结果对比如表2所示。

由表2可以看出，改进BP算法对车辆减速器的诊断误差比传统的BP算法诊断误差要低，准确率可达到96%，所以利用改进的贝叶斯BP算法优化BP神经网络的各个参数，不仅可以显著提高BP网络的收敛精度和效率，而且泛化能力较传统的BP神经算法要强。

4 结论

针对T•JK(Y)型驼峰车辆减速器故障靠人工经验判断维修效率低，首次提出了用改进BP神经网络对驼峰车辆减速器进行故障诊断。仿真结果表明：所采用的改进BP算法训练具有精度高，收敛速度快，泛化能力强等特点，提高了对减速器故障的判别速度和准确性，从而有效缩短了维修时间。为了更加精确地查找和控制故障，下一步还需对更加复杂的综合故障进行研究。

表2 两种算法结果比较

[1] 侯忠馨，王庆贤，祝曦，等.涡流制动技术在铁路驼峰调节溜放速度的应用研究[J].铁道科学与工程学报，2015，12(4):923-928.

[2] 李岱峰，郭祥熹，张朴.T·JK、T·JY系列车辆减速器[M].北京:中国铁道出版社，2002.

[3] 周东华，叶银忠.现代故障诊断与容错控制[M].北京：清华大学出版社，2000.

[4] 中华人民共和国铁道部.TB/T 2845—2007车辆减速器技术条件[S].北京：中华人民共和国铁道部，2007.

[5] 黄启学.驼峰车辆减速器常见问题的改进[J].铁道通信信号，2013(1):54-55.

[6] 李鹏.基于贝叶斯理论的神经网络算法研究[J].光机电信息，2011，28(1):28-32.

[7] 聂晴晴.贝叶斯改进BP神经网络在织物染色配色中的应用研究[D].青岛：青岛大学，2009.

[8] 马进杰，李涛，郭明.TJK2型驼峰车辆减速器表示轴防折断改造[J].铁道通信信号，2014(7):29-30.

[9] 邱战国，郭祥熹，魏锋.车辆减速器红光带故障分析与处理[J].铁道通信信号，2014(11):39-42.

[10]中华人民共和国铁道部.铁运[2008]142号铁路信号维护规则[S].北京:中国铁道出版社，2008.

[11]丁恩山.驼峰重载车辆减速器可靠性技术及维修重点的研究[D].北京：中国铁道科学研究院，2014.

[12]郭富强，吴丹，商跃进，等.T·JK4加强型车辆减速器制动钳疲劳强度分析[J].机车电传动，2011(2):28-30.

[13]郭祥熹，甄建铁.T.JK3—A(50)型车辆减速器研究与应用[J].中国铁道科学，1998，19(3):51-56.

Research on Fault Diagnosis of Hump Car Retarder Based on Improved BP Neural Network

JIANG Xue-jie， LI Guo-ning

(College of Automation & Electrical Engineering， Lanzhou Jiaotong University， Lanzhou 730070， China)

The retarder is the main part of the control speed system of the hump yard. With the development of high speed railway and the increase of railway freight volume， the capacity of break-up and make-up of the marshalling yard is increased and the utilization and fault of the retarder is increased simultaneously， while the low efficiency of the maintenance workers fails to meet the current requirements of freight humping， which addresses more on humping control and effective coupling. Therefore， based on the field data， BP neural network model is established for simulation training and the fault location of T•JK (Y)2， 3 of hump retarder is diagnosed precisely. The results show that the fault diagnosis accuracy rate reaches 96%．

Hump; T•JK (Y) car retarder; BP neural network; Fault diagnosis

2016-04-14；

2016-05-17

国家自然科学基金地区项目(61164010)

姜雪杰(1990—)，男，硕士研究生，主要研究方向为编组站驼峰场车辆减速器故障诊断，E-mail：15117010482@163.com。

李国宁(1959—)，男，副教授 主要研究方向为交通信息工程及控制以及编组站驼峰场，E-mail：372514424@qq.com。

1004-2954(2016)12-0135-05

U284.68

A

10.13238/j.issn.1004-2954.2016.12.030