几何画板在高中数学教学中的应用研究
2016-12-29朱贤梅
朱贤梅
【摘 要】在高中数学教学环节中,数学教学难度较高,知识点较为抽象,时常需要借助各类教学工具来完成教学。几何画板是一种较为确切的数学制图工具,伴随着科学技术的教育领域运用程度增加,几何画板于高中数学教学中得到了广泛运用。本文首先对几何画板在高中代数教学中的作用,其次对几何画板在代数教学、立体几何、平面解析几何中的应用进行介绍。希望对高中数学教学水平的提升,贡献一份力量。
【关键词】几何画板;高中数学教学;研究
几何画板是最为常用的数学教学工具,以点、线、面为根基,且在数学中借助这些元素进行计算,展现出其它不一样复杂的几何图形,从而起到辅助教学的作用。几何图形的建立,可以更加明显、直观的展现数学知识,方便学生对数学知识的学习。与此同时,还能够更好的培育学生发散、创新性思维[1]。
1几何画板在高中数学教学中的作用
1.1几何画板特征介绍
几何画板具有简单、明了、短效、朴实等特点,在制图环节操作较为简便,能够大量使用有限的资源,完成各种组合变化,且在学习掌握几何画板的使用时,使用较为简单,并不需要耗费太多的时间和精力。此外,几何画板所需投入的人力资源较少,在利用几何画板绘图课程时,教师并不需要耗费太多的时间,一般来说几分钟就能绘制出一个较好的课件,对计算机掌握程度要求不高。另外,几何画板界面比较简单,绘制出的课件并不需要大量的装饰,可以很好的展现出绘制人的主体表达思想,同时还能直接反应问题,让学生对问题一目了然[2]。
1.2几何化的作用介绍
几何画板能够为数形联合创造良好的便捷通道,能够为几何模型供应相应的绘制条件,进而很好的解决学生绘图困难的问题,同时也能够直接反应学生的动态情况,进而绘制出能够激发学生兴趣的图形,进一步带动学生绘图的主动性和积极性,且能够找出问题的根本所在。此外,几何画板的预算功能可以对问题的了解,来反应问题的本质,进而能够令学生更加全面的掌握知识点,并实时了解难点问题。
2几何画板在高中代数教学中的运用
函数是高中数学最基本的理念,其理念和思维方式涵括高中数学的所有部分,且函数是以运动改变的观念对来展现世界关系的变化。华罗庚曾表示:数缺形则不够直观,形缺少数很难入微。解析式和图像是函数的两种表达形式,二者需要进行对照。为解决数形结合存有的问题,在函数的以往教学中,教师主要以手工绘图为主,但手工绘图不够准确,速度较慢。而使用几何画板则能快速体现功能上的变化,大幅度提升课堂成效。具体而言,可利用几何画板依照函数的解析式快速绘制图形,且能在同一坐标系内画出多个函数,例如:在同一直角坐标系中画出y=x2,y=x3和y=x1/2的图形,对比各图形的位置和图形,汇总函数的属性。并作出包括有关参数的函数图形,在参数出现变化时函数也发生改变,例如:在讲解函数y=Asin(ωx +φ)图形时,以往教学仅能把A,ω,φ带入有限值,来观察各个状况下图形变化关系。
几何画板在高中代数的其它方面用途较多,比如:根据图形对不等式性质、解法、理论进行直观解析,由半径不超过半弦表明不等式a+b≥2等。同时,在介绍数量极限理念时,绘制出an=10n图形时,观看曲线的变化情况,且借助几何画板的绘制能力以项数值,及对这一项0的绝对值列表,令学生能够直观的了解这一理念。
3几何画板于立体几何教学中的运用
立体几何是在学生已掌握的平面图形基础上探讨空间图形的性质,其研究的理论基础是公理,直接根据图形的点、线、面的关系来探究图形的性质。自平面几何的理念过渡到立体几何,需要一定的时间。初中时期在学习立体几何时,绝大多数学生没有丰富的空间想象能力,根本原因在于学生是借助二维图形来感受想象的三维图形,而二维平面无法成为三维图形的实际写照,平面绘图的立体图形由于受到视觉的影响,很难观察整体,空间形式的抽象性较大。例如:两条相互垂直的直线并不一定画成直角的直线。正方体的各个面,均无法画出正方形。这样造成学生无法依照歪曲图像来了解实际情况,从而给学生学习立体几何造成困难。而使用几何画板图像,则能够将各元素间的位置有效联系起来,令学生能从各个角度观察图像,从而帮助学生了解和接受立体几何,并充分发挥其发散性思维能力。
4几何画板于平面解析几何教学中的运用
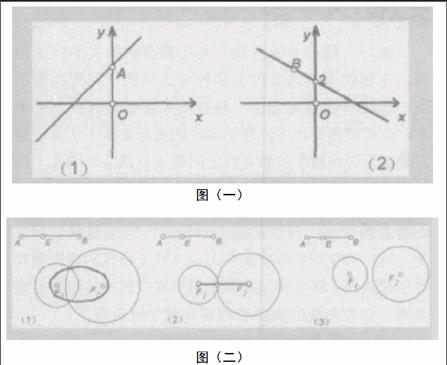
平面解析几何时使用代数方法来探究几何问题的数学学科,其主要探究的问题是基本思想和基本方法,依照现有条件,选取恰当的坐标系,根据形和数之间的对照关系,解答出平面曲线方程,将形的问题转变为数来探讨,在经过方程,探究平面曲线的性质,将数的探究转换为形来探讨。而曲线中各类几何量受到各类因素约束而产生变化,造成点、线依照不同的方式运动,曲线和方程的对照关系较为抽象,学生很难理解,显然展现几何图形和运动的整体过程在解析几何中变得异常关键。几何画板又以自身强大的估算能力和图形图像结合能力,在解析几何的教学中大量运用。例如:其能够将各种类型方程的曲线,借助动态图像追踪,来显示对象的运行轨迹,在拖动点和线的过程中,实现图形的变化,以此探究两个或两个以上曲线之间的位置联系。例如:在介绍平行直线系y=x+b或中心直线系y=kx+2过程中,如图一,在拖动图(1)内a点和图(2)内b点时,能够相对应的看见一组斜率为1的平行线与过定点(0,2)的一条直线,不包括y轴。再例如:在介绍椭圆含义时,可将两定点F1和F2距离之和设定为定值轨迹(如图二所示),以F1为圆心,AE为半径,F2为圆心,AE为半径,那么两圆之间的交点轨迹则满足要求。先安排学生估测这样点的轨迹图形时什么,然后让学生发表自身观点,教师演示图二(1),让学生明白是椭圆,同时老师使用鼠标拖动B,令|AB|=|F1F2|如图二(2),学生开始仔细思考,从而得出图二(3)的情形。在这个过程中,学生经历了椭圆的形成原理过程,也提升了独立思考能力。
图(一)
图(二)
5结语
整体而言,利用几何画板开展数学教育活动,借助实际的感悟信息体现,令学生加深印象,令学生不将学生当作单纯的知识去学习,而是将其实体化来掌握,从而大幅度提升学生学习乐趣,培育学生学习兴趣,进一步提升数学教学效率。
参考文献:
[1]何敏藩,余剑华.几何画板在解析几何教学中的创新应用[J].电脑知识与技术.2016,01(10):10-11.
[2]苏建国.“几何画板”在高中几何教学中的应用刍议[J].数理化学习.2015,02(11):22-23.
