基于TRIZ理论的双向弓形夹结构优化设计

杜春宽

(无锡商业职业技术学院，无锡 江苏 214153)



基于TRIZ理论的双向弓形夹结构优化设计

杜春宽

(无锡商业职业技术学院，无锡 江苏 214153)

标准弓形夹只能夹持单组工件，而不能夹持多组、有相对位置要求的工件，其应用范围受到限制，针对这一问题，利用TRIZ理论寻求解决方案，设计一种具有双曲线结构的双向弓形夹，可双侧夹持工件，扩大弓形夹的应用范围，并对双向弓形夹受力状态进行有限元分析，结果证明弓形夹所受应力分布较均匀，夹持能力得到显著提高。

TRIZ理论；弓形夹；优化设计；有限元

标准弓形夹是一种用来夹持两件或两件以上工件的夹紧装置，一般应用在对接工件的焊接或黏接中。标准弓形夹夹持工件时，通过旋进螺杆对工件施加以垂直于接触面的夹紧力来夹紧工件，根据力的作用与反作用公理，工件也会对标准弓形夹施加大小相等、方向相反的反作用力。弓形夹所受反作用力产生的应力分布不均匀，限制了弓形夹的夹持能力[1]，本试验利用TRIZ理论分析其技术矛盾，利用发明原理改进结构设计，提高了弓形夹的夹持能力，并扩大了应用范围。

1 TRIZ理论及其矛盾分析法

TRIZ理论(theory of inventive problem solving，TIPS)是前苏联发明家阿奇舒勒(G.S.Altschuller)于1946年开始带领他的团队经过对世界各国约250万份优质专利文献的分析、比较、归纳和研究，提出了一套具有完整体系的发明问题解决理论和方法，主要包括39个通用工程参数、40条发明原理、76个标准解和效应知识库[2]。TRIZ理论适用于设计人员掌握发明创造的规律，提高创新设计能力[3-4]，TRIZ理论在现代制造业中获得了广泛应用，越来越受到企业和科技人员的重视[5]。TRIZ理论解决问题流程，见图1。

TRIZ理论认为矛盾存在于各种产品或技术系统中，解决矛盾冲突是发明问题的核心，未解决矛盾冲突的设计不是创新设计。TRIZ理论将工程矛盾分为技术矛盾、物理矛盾和管理矛盾，管理矛盾可以通过分析转化为技术矛盾或物理矛盾；物理矛盾是指对技术系统中的某一组件(元件)的参数(属性)提出了截然不同的需求；技术矛盾是指一个技术系统中某一个参数(特性)得到改善的同时，导致另一个参数(特性)发生恶化而产生的矛盾，其解决首先是确定欲改善的参数和被恶化的参数，然后从矛盾矩阵表中查找推荐的发明原理，再经分析、遴选出有益的发明原理，最后根据发明原理确定解决方案。

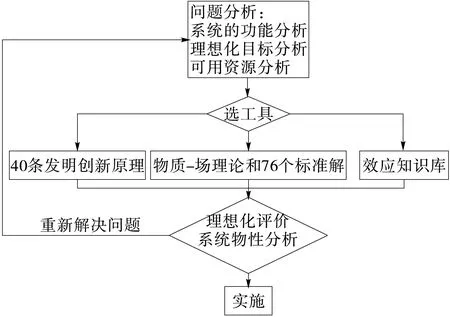
图1 TRIZ理论解决问题流程图Figure 1 The flow chart of TRIZ theory to solve the problem

2 基于TRIZ理论的双向弓形夹设计

2.1 标准弓形夹存在的问题

通过文献[1]可知弓形夹在夹持工件时，在反作用力作用下，弓形夹各处所受应力相差较大，在拐角内侧应力最大，即危险截面在弓形夹拐角处，改善其应力分布，就能提高弓形夹夹持工件的能力；标准弓形夹只能单侧夹紧、固定一组工件，但对于多组工件、组件和组件之间有相对位置要求的夹持，标准弓形夹很难满足要求。

2.2 设计过程中存在的矛盾

弓形夹在夹持工件时，如果增大夹紧力，那么工件对弓形夹的反作用力也增大，弓形夹危险界面处所受应力也随之变大，如此工况，强度和应力构成了一对技术矛盾[6]，应力是被恶化的参数，而强度是欲改善的参数，构成了第1组技术矛盾。

标准弓形夹不能夹持多组工件、使工件组保持一定的位置关系，所以弓形夹需要重新设计，改善弓形夹的应用性、可操作性，能够夹持多组工件，且保持相对位置要求。相对于标准弓形夹，新弓形夹的制造工艺需要重新制定、工艺装备需要重新购置等，增加了制造成本和加工难度，所以改善弓形夹的可操作性，势必导致可制造性的降低，所以可操作性和可制造性构成了技术矛盾，可操作性是欲改善的参数，可制造性是被恶化的参数，构成了第2组技术矛盾。

2.3 基于TRIZ矛盾矩阵的双向弓形夹设计方案

根据上述2组技术矛盾，可从矛盾矩阵表中查得推荐的7个发明原理(见表1)，并不是所有的发明原理对问题解决有帮助，经分析比较发现，发明原理5和发明原理3对问题的解决是有益的。增强弓形夹的可操作性，使其能够夹持多组工件，且能保持相对位置。然而一个标准弓形夹只能夹持一组工件(见图2)，那么夹持多组工件就需要多个弓形夹，但弓形夹是个体存在，不能使工件组保持相对固定的位置关系，根据第5条发明原理 “把确定的多个系统或操作中的相同类型或协同作业结合在一起”，本文把两个弓形夹合并成一个双向弓形夹，可夹持两组工件，且能使工件保持固定的位置关系(见图3)。

弓形夹在夹持工件时，所受应力分布不均，最大应力在弓形夹拐角内侧，提高弓形夹的夹紧力就会使弓形所受的应力增大，危险截面的应力首先达到应力极限值，而弓形夹其它部分应力还没有达到应力极限值，在弓形夹危险截面处就会发生塑形变形、开裂等失效形式，说明应力分布不均限制了弓形夹的夹持能力，弓形夹各部分没有发挥最大效能，要提高弓形夹的夹持能力，使弓形夹的应力分布均匀，原有的直线轮廓无法达到这一要求，见图4(a)。第3条发明原理“物体的每个部分都应处于最有利其发挥自身作用的状态”给予我们启示，弓形夹受力大的地方，其截面应大些，在工形夹受力小的地方，其截面应小些，这样弓形夹所受应力分布均匀，各部分发挥自身的作用，所以设计了一种双曲线轮廓的双向弓形夹，见图4(b)，由于双曲线光滑平顺，不会产生应力集中，从而提高了强度，节省了材料，使材料发挥最大效能。

表1 矛盾矩阵分析Table 1 Analysis on contradiction matrix

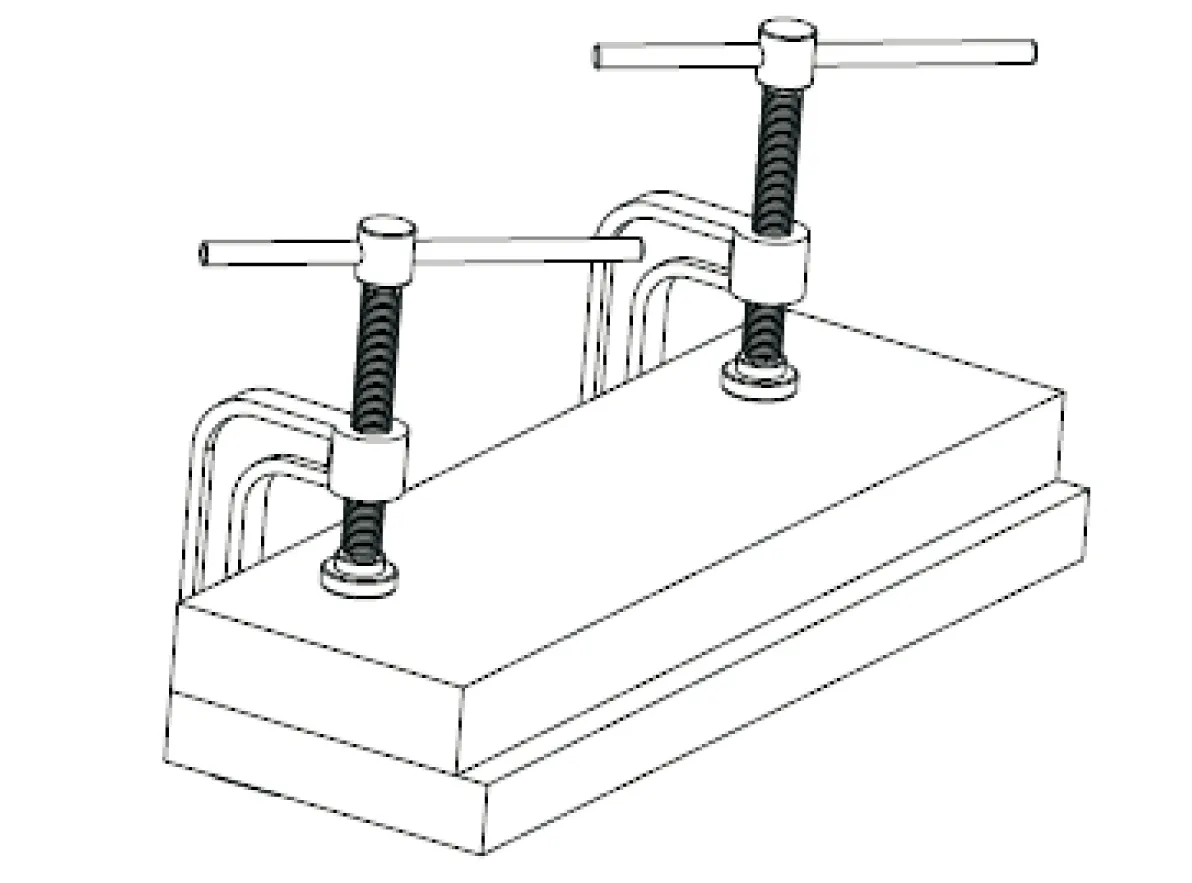
图2 标准弓形夹Figure 2 Standard cramp frame

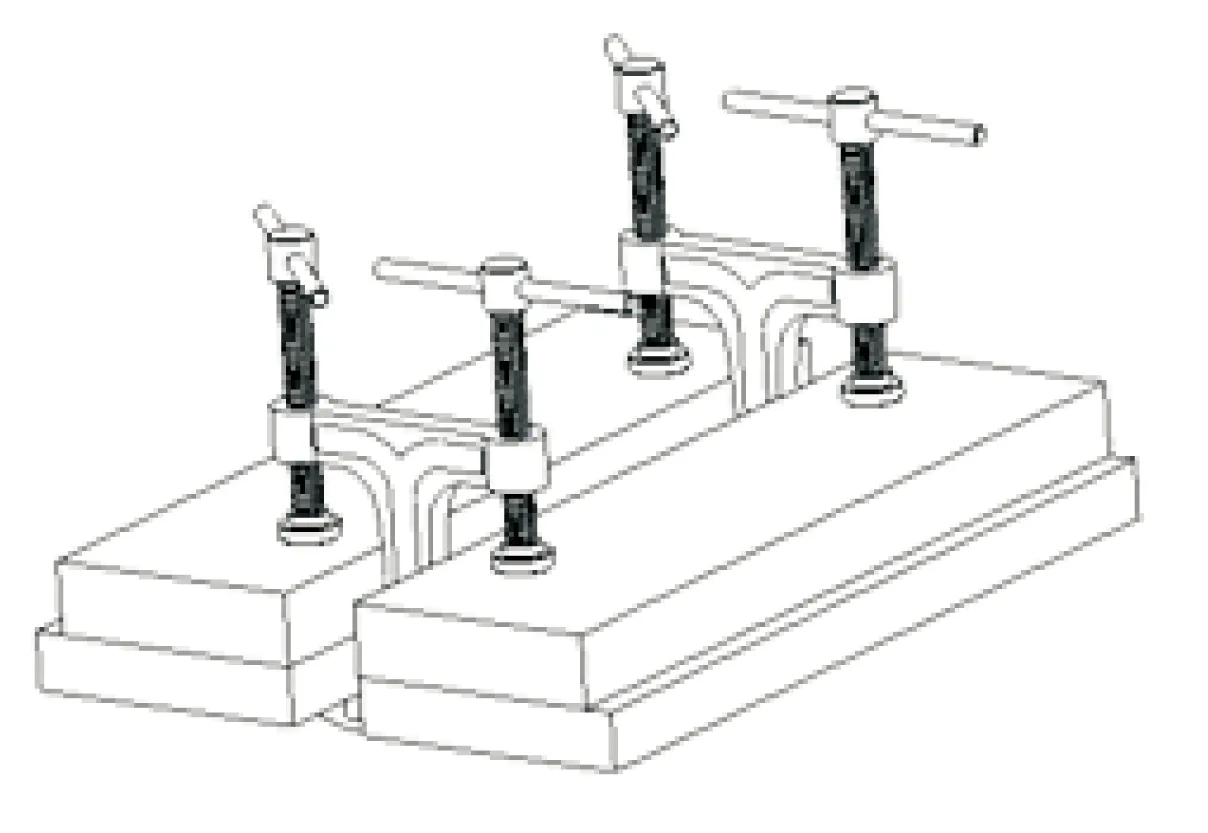
图3 双向弓形夹Figure 3 Bidirectural cramp frame

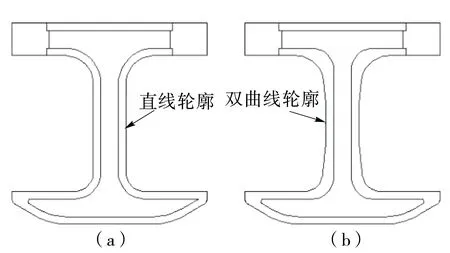
图4 弓形夹轮廓线比较Figure 4 Comparison of the profile of cramp frame

3 双向弓形夹设计结果分析与比较

以标准弓形夹M20为参照，设计双向弓形夹M20[7]，利用建模软件和有限元分析软件进行等效应力仿真，定量分析设计结果，验证采用TRIZ理论设计方案的合理性。

3.1 不同轮廓线双向弓形夹的应力分析和比较

有限元分析是行之有效的工程分析手段，能适应各种复杂形状构架的静力学分析[8-10]。利用creo软件进行建模，ansys workbench 软件对双向弓形夹进行有限元分析，材料采用：ZG310-570，屈服应力为310 MPa，抗拉强度为570 MPa，拉、压许用应力同取为155 MPa，弹性模量E=200 GPa,泊松比μ=0.3，密度为7 850 kg/m3。对直线轮廓双向弓形夹和双曲线双向弓形夹施加相同的约束和载荷，在弓形夹下端两侧施加固定约束，上端两侧螺纹孔处分别施加6 547.8 N载荷[1]，由于工件结构简单，不复杂，为了计算结果精确，网格划分采用整体网格控制，相关度设置为100，尺寸控制高级选项打开，为on:curvature，相关度中心设置为medium；在static structural模块进行等效应力有限元分析，图5(a)是采用直线轮廓的双向弓形夹M20的应力分布云图，可以看出，应力分布不均匀，最大等效应力分布在立柱内侧拐角处，达到了173 MPa，图5(b)是双曲线轮廓的双向弓形夹M20应力分布云图，与直线轮廓的弓形夹相比，应力分布相对较均匀，其最大等效应力降低了65 MPa，接近38%的降幅，说明轮廓线采用双曲线改善了双向弓形夹承载结构，使弓形夹的承载能力得到了显著提升。

3.2 立柱轮廓线参数优化

现对双曲线轮廓进一步优化，通过不同参数的对比，获得较理想的结构。以双曲线双向弓形夹M20为例加以阐述。

图5 双向弓形夹两端施加6 547.8 N载荷时的 等效应力云图

Figure 5 Equivalent stess nephogram of bidirectural cramp frame under the load of 6 547.8 N

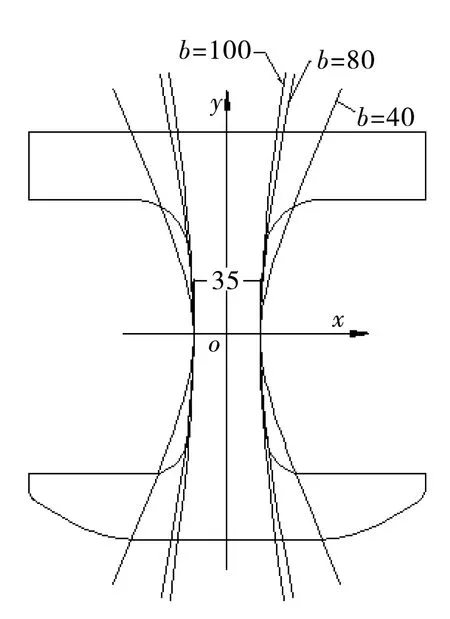
图6 双曲线轮廓Figure 6 Hyperbolic profile of cramp frame

3.2.2 双曲线参数优化 从图6还可以看出，当b值取小值时，曲率半径减小明显，弓形夹材料增加较多，夹持空间变小，且经济性降低，所以b值不宜选择小值。b值分别选取70，80，90，100，110，120，其他结构尺寸参数不变，利用creo进行建模，采用ansys workbench 软件进行有限元分析。双向弓形夹两侧夹持工件，施加的载荷和边界条件和图5应力分析相同，通过有限元分析可知，最大等效应力分布在拐角内侧，其大小受到双曲线b值参数大小的影响，从图7最大等效应力参数曲线可以看出，随着b值增大，最大等效应力也随之增大，说明b值增大，双向弓形夹的承载能力下降；从图7质量曲线可以看出，b值增大，双向弓形夹质量随之减小。从质量参数曲线和最大等效应力参数曲线分布趋势来看，b值在80和90之间较为合理，双向弓形夹结构得到了优化，承载能力得到了有效提升，且结构尺寸变化不大(如图6b=80曲线)，不影响零部件的装夹。

4 结论

(1) 利用TRIZ理论设计了一种双曲线结构的双向弓形夹，在夹持工件时，其所受应力分布较均匀，提高了弓形夹的夹持能力，且可双侧夹持工件，使工件保持一定的位置关系，扩大了弓形夹的应用范围。

(2) 通过TRIZ理论设计的双向弓形夹是标准弓形夹的改进和升级，是标准弓形夹的重要补充，可形成系列、通用性产品，满足不同行业对弓形夹的需求。

图7 危险截面应力值曲线和双向弓形夹质量参数曲线图Figure 7 The stress curve of minimum life section and curve of quality parameters

[1] 杜春宽. 弓形夹的改进设计及等强度设计[J]. 煤炭技术, 2015, 34(2): 233-235.

[2] 张建中, 李坤, 张树君, 等. 可移动切断机的设计与仿真[J]. 食品与机械, 2011, 27(5): 131-133.

[3] 陶义, 王宗彦, 吴淑芬, 等. 基于TRIZ矛盾分析法的重型卡车弹簧支架轻重化设计研究[J]. 机械设计与制造, 2015(3): 188-191.

[4] CONG H, TONG L H. Grouping of TRIZ Inventive Principles to facilitate automatic patent classification[J]. Expert Systems with Applications, 2008, 34(1): 788-795.

[5] 候磊, 芮延年, 朱兴满. 基于TRIZ理论的干燥过滤器夹紧装置结构优化设计[J]. 机械设计与制造, 2011(7): 240-242.

[6] 李正峰, 王吴光, 陈玉梅. 基于TRIZ理论的锤式破碎机新型锤头研究[J]. 矿山机械, 2015, 43(12): 87-89, 91.

[7] 杜春宽. 一种新型弓形夹: 中国, CN201420873822[P]. 2014-12-30.

[8] 李正峰, 杜春宽, 王新琴. 基于 TRIZ 理论的套筒联轴器改进设计[J]. 机械传动, 2016(3): 85-87.

[9] 马军, 彭博, 路迪, 等. 高空作业车工作装置整体性能有限元优化设计研究[J]. 机械设计, 2015, 32(6): 56-60.

[10] CHANDRA SAKARA N, HAISLER W E. Finite element analysis of hertz contact program fiction[J]. finite elements in analysis and design, 2003, 41(2): 117-127.

Optimal design for bidirectural cramp frame based on TRIZ theory

DU Chun-kuan

(Wuxi Institute of Commerce, Wuxi, Jiangsu 214153, China)

It was well known that standard cramp frame can only clamp a group of workpieces, without the ability to catch many groups of workpieces with related position constraint. To solve this problem, a design solution based on TRIZ theory as well as an inventive principle were proposed in this study. A bidirectural cramp frame with hyperbolic structure was designed, and it could clamp workpieces on both sides. Therefore, the application range and fields of this new kind cramp frame were expanded. Moreover, the bidirectural cramp frame was also analyzed and optimized using the finite element method. Finally, simulation results showed that both the bearing capacity of the bidirectural cramp frame and its stress distribution were improved.

TRIZ theory; cramp frame; optimal design; finite element method

无锡商业职业技术学院一般课题(编号：SYKJ16B06)

杜春宽(1977—)，男，无锡商业职业技术学院讲师，硕士。E-mail：66257357@qq.com

2016—07—08

10.13652/j.issn.1003-5788.2016.11.020