两段变直径桩的解析分析及工程应用

何喜洋，周雷靖，胡云霞

(中国能源建设集团广东省电力设计研究院有限公司，广州 510663)



两段变直径桩的解析分析及工程应用

何喜洋，周雷靖，胡云霞

(中国能源建设集团广东省电力设计研究院有限公司，广州 510663)

桩在水平荷载作用下的内力与位移计算，桩基设计规范推荐使用m法。m法的缺点是，当为了显著增大桩的水平承载力而在靠近承台的区域将土进行换填时，该处的土实际的刚度与其假定相距甚远。采用2K法进行水平荷载作用下桩的内力与变形分析，重点把握土的两个侧向弹簧刚度。2K法在工程中的应用是广泛的：承台附近土换填或加固，或将桩顶附近弯矩较大的桩身部分设为更大的直径，上段桩土弹簧刚度将增大，在一定的水平荷载作用下，桩顶位移将减小，桩的水平承载力得到提高而节省工程造价；如果在计算模型中未建立桩单元而欲求得桩顶反力，则采用变直径桩解析分析获得的位移函数和内力函数可计算桩的内力用于配筋；对于箱型基础、大型筏板基础，可较为精确地考虑其对桩顶的嵌固作用而提高桩的水平承载力；上部结构的刚度使得桩顶部有侧向支撑，桩身弯矩变小，也可优化桩基设计；对于桩基上的动力机器和块式基础，可以认为块式或承台是上段大直径桩，由此获得的上段桩侧向土弹簧刚度将非常可观，可用于优化桩基设计。如果考虑将桩建入计算模型，可以通过本方法得出的四个刚度参数输入到弹簧支座刚度矩阵中，能够节省桩建模及其内部单元带来的大自由度，计算模型更容易维护，其这也是一体化建模发展过程中的一个重要里程碑。

2K方法；变直径桩；解析分析；弹簧刚度；桩单元

关于桩在水平荷载作用下的内力与位移计算，桩基设计规范[1]推荐使用m法：即假定桩侧土的弹性刚度随着深度的增加而线性增大。m法的缺点是：第一，当为了显著增大桩的水平承载力而在靠近承台的区域将土进行换填时，该处土的刚度与其假定相距甚远；第二，m法没有解析解(即写不出公式，一般取用无穷级数解的前面部分作为近似解)，如果要采用m法的公式还不如直接用有限元建模来得简单(建模的好处不言而喻，适用于任何形式的土层参数或本构关系，但计算模型自由度增大，难于调试与管理)。因此，类似的情况也有所谓的常数法刚度法[2]。

本文提出一种全新的常数刚度方法(比常数刚度法增加一个弹簧刚度K，以下简称2K法)用于两段变直径桩，并据此编制了计算软件。其特点如下：

1)在靠近承台附近的土被换填并加固后，常数刚度法能克服m法的缺点，其刚度不再是零而可以是任意合理的、可以实现的刚度值。

2)众所周知，桩长往往不是桩水平承载力的决定因素，实际上决定桩水平承载力的正是上述被加固的、接近桩顶的土层，常数法刚好抓住了这个重点；同时，桩顶附近弯矩较大的部分可以设为更大的直径，其与土层的接触面积也增大(相当于土的刚度再次增大)。

3)2K法比m法简单，当桩径分段变化时更便于解析分析。2K法能获得微分方程的解析表达式，其求解不需要采用近似方法或者借助计算机程序建模。

何喜洋,等：两段变直径桩的解析分析及工程应用

1 计算模型的解析分析

图1所示2K变直径桩力学模型实质为文克勒弹性地基上的梁，取微元段(见图2)作受力分析后可知其数学模型是一常系数四阶齐次线性微分方程，主要关系式和方程如式(1)～式(4)所示。

图1 水平荷载作用下两段变直径桩的计算模型Fig. 1 Calculation model of 2K-Pile

(1)

EI1w‴(x)=-V(x)；EI2w‴(x)=-V(x)

(2)

(3)

(4)

图2 微元受力分析Fig. 2 Element force analysis

引入λ后，式(3)及式(4)可以改写为：

（1）经费拨付方式：服务项目立项后将拨付60%的项目经费，待项目结项评估合格后，再拨付剩余经费；若未通过终期评估的项目单位，将扣除剩余的40%用于奖励优秀项目；区县（自治县）民政局配套经费在项目立项后2个月内到位。

(5)

(6)

根据式(5)，第1桩段通解为：

w(x)=eλ1x(A1cosλ1x+B1sinλ1x)+

e-λ1x(C1cosλ1x+D1sinλ1x)

(7)

第2桩段通解为：

w(x)=eλ2x(A2cosλ2x+B2sinλ2x)+

e-λ2x(C2cosλ2x+D2sinλ2x)

(8)

上式中的待定常数，可由荷载和边界条件确定。

2 位移函数的各阶导数

为了通过边界条件求解待定常数，必须首先获得位移函数的各阶导数；同时，这些导数或者导数与桩截面刚度特征常数的乘积就是我们需要求解的弯矩和剪力。以下为第1桩段的求导情况：

从式(12)得知求导过程正确。同样道理，第2桩断位移函数的各阶导数如下：

图3 变直径桩的系数方程组(8×8)Fig. 3 Coefficient equations for variable diameter pile(8×8)

3 边界条件处理

通过边界条件(2)的处理，可以获得4个关于系数的方程。在变截面处，位移相等、转角相等、弯矩相等、剪力相等。

1)位移相等

A1+C1=A2+C2

(16)

2)转角相等

λ1B1+λ1A1-λ1C1+λ1D1

(17)

3)弯矩相等

(18)

4)剪力相等

通过边界条件(1)和(3)的处理，可以获得另外4个关于系数的方程：左端弯矩(即桩顶弯矩)为M0；左端剪力为V0；右端嵌固，水平位移为零；右端嵌固，转角为零：

4 系数方程组求解及程序设计

处理边界条件后将获得关于系数A1～D1、A2～D2的八元一次线性方程组，其矩阵如图3所示。该方程组很容易通过EXCEL或者计算程序进行求解。笔者已同时做了这两项工作，如图4所示。通过计算表格或者程序，输入桩和土的参数就能获得关于坐标X的位移函数、转角函数、弯矩函数及剪力函数。

可以用建模方式进行上述解析分析过程的检验。本文采用SAP2000建立有限元模型：上段桩直径为1 000mm，长度为5m，弹簧刚度20 000kN/m2(注意与桩的直径有关)；下段桩直径为500mm；长度为15m，弹簧刚度15 000kN/m2；桩顶剪力20kN，桩顶弯矩0.0kN；SAP2000的单元划分非常细致，单元长度0.1m。SAP2000与计算程序的结果对比如表1所示。

对比分析表明，程序计算结果是正确的，而且应该是精确解。SAP2000的计算结果与程序的差异是因为单元划分不够细致造成。同时，我们从两种边界条件的计算结果中看到，如果桩足够长，由于土弹簧的支承作用，使得桩身变形大大减小，桩顶的内力很难往下传递，因此，两种边界条件下的计算结果十分接近，桩端是否嵌固已经不再重要。

表1值得注意的是，位移为单位mm；内力单位kN和m；表中选择了X=-L处的位移与最大内力进行比较。

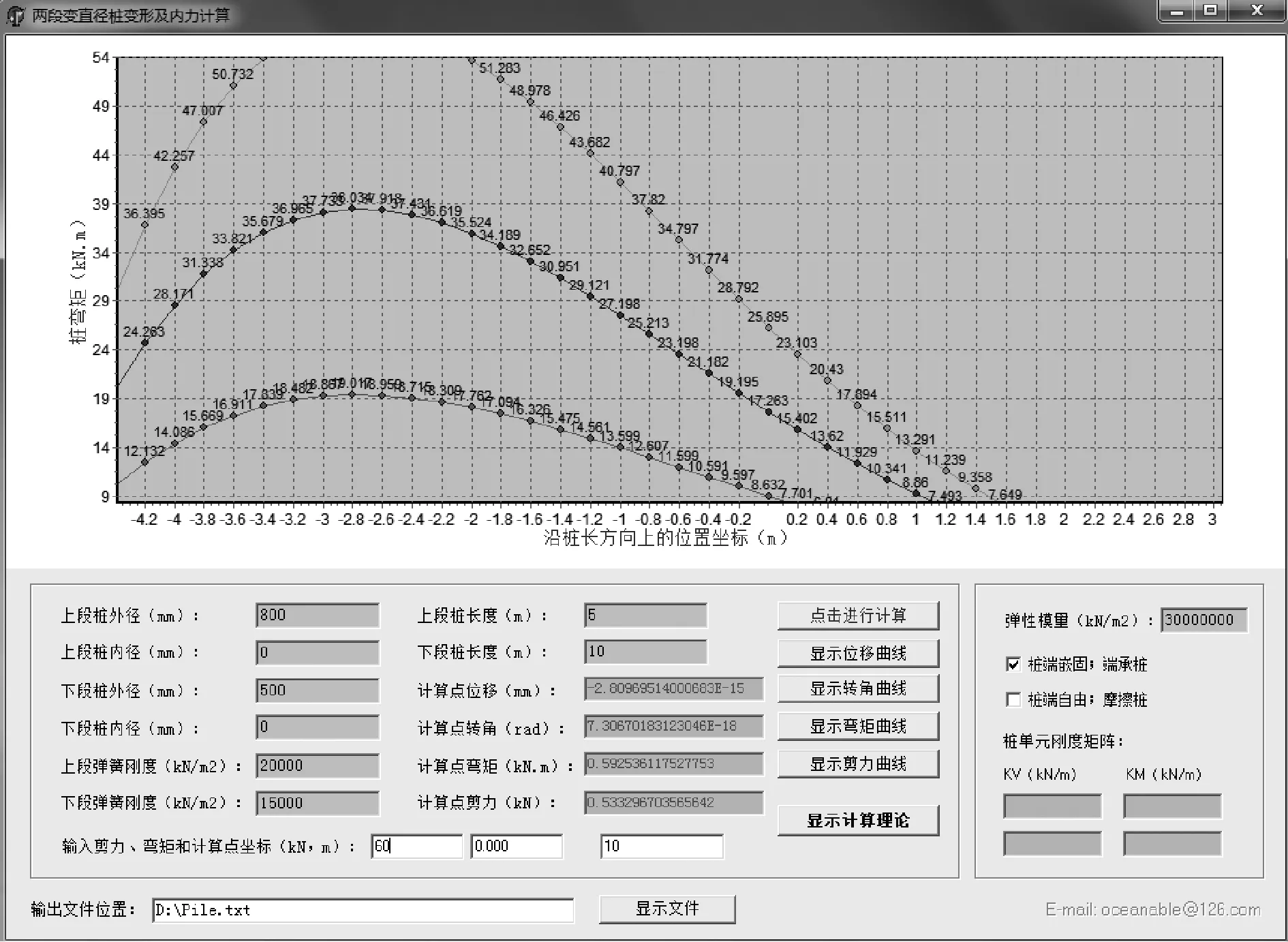
图4 变直径桩的系数方程组(8×8)Fig. 4 Coefficient equations for variable diameter pile

表1 变直径桩的计算程序与SAP 2000计算结果对比

Tab. 1 Program calculation results contrast with SAP 2000

边界条件桩底端嵌固桩底端自由比较项目位移转角最大弯矩最大剪力位移转角最大弯矩最大剪力SAP20000583—197818830584—19781883计算程序0599—204420000599—20432000

5 结论

采用2K法进行水平荷载作用下桩的内力与变形分析，关键的参数是土的两个侧向弹簧刚度。要确定弹簧刚度最好的办法是通过桩基静载荷试验，类似于m值的确定方法。如果没有进行试验，可以按照土的类型根据桩基规范[1]中的m值和土层的厚度近似计算K值。2K法能够解决工程实践中的许多问题：

1)如前所述，桩长往往不是桩水平承载力的决定因素，决定桩水平承载力的正是被换填或加固的、接近桩顶靠近承台的土层，将此部分的土换填或加固(也只需将此部分土层加固)，上段桩土弹簧刚度将增大。在一定的水平荷载作用下，桩顶位移将减小，桩的水平承载力得到提高而节省工程造价。

2)同样地，桩顶附近弯矩较大的桩身部分可以设为更大的直径，其与土层的接触面积将增大，也相当于土的刚度增大。桩的水平承载力得到提高而节省工程造价。

3)如果在计算模型中未建立桩单元而欲求得桩顶反力，则变直径桩解析分析获得的位移函数和内力函数可计算桩的内力用于配筋；对于箱型基础、大型筏板基础，可较为精确地考虑其对桩顶的嵌固作用而提高桩的水平承载力；上部结构的刚度使得桩顶部有侧向支撑，桩身弯矩变小，也可优化桩基设计。

4)对于桩基上的动力机器和块式基础，可以认为块式或承台是上段大直径桩，由此获得的上段桩侧向土弹簧刚度将非常可观。可优化桩基设计。

(ContinuedonPage101)(ContinuedfromPage91)

5)如果考虑将桩建入计算模型，可以通过本方法得出的四个刚度参数输入到弹簧支座刚度矩阵中，能够节省桩建模及其内部单元带来的大自由度，计算模型更容易维护。笔者认为，这也是一体化建模(上部结构、基础、地基在同一个计算模型中)发展过程中的一个重要里程碑。

[1] 高大钊.土力学与基础工程 [M]. 北京：中国建筑工业出版社, 1998.

[2]中华人民共和国建设部.建筑桩基技术规范：JGJ 94—2008[S].北京：中国建筑工业出版社, 2008.

(责任编辑 张春文)

Analytical Analysis and Practice of Two-segment Variable Diameter Pile

HE Xiyang, ZHOU Leijing, HU Yunxia

(China Energy Engineering Group Guangdong Electric Power Design Institute Co., Ltd., Guangzhou 510663, China)

The internal force and displacement of piles under horizontal load are calculated, and the m method is recommended for the design of pile foundation. The disadvantage of m method is that the stiffness of the soil is very far from the assumption that the soil is replaced by the soil in the region near the cap when the horizontal bearing capacity of the piles is significantly increased. In this paper, 2Kmethod is used to analyze the internal force and deformation of piles under horizontal load, and the two lateral spring stiffness of the soil. The application of 2Kmethod in engineering is widely: the pile foundation near the soil for filling or reinforcement, the larger diameter of the pile body, the upper part of the pile body is set to increase, the pile foundation displacement will be reduced, and the pile's bearing capacity can be improved, and the internal force of pile can be calculated, It can be more accurate to consider its effect on the pile top, the horizontal bearing capacity of piles, the pile bending moment of the pile top, the bending moment of piles, the pile bending moment, the pile body bending moment, the pile body bending moment, and the pile foundation design. If the pile is built into the calculation model, the four stiffness parameters can be obtained by this method, and it can save the large degree of freedom of the pile modeling and its internal unit. The model is more easy to maintain, and this is an important milestone in the development of integrated modeling.

2Kmethod; variable diameter pile; analysis; spring rigidity; pile element; stiffness matrix

2016-01-08

何喜洋(1978)，男，广东增城人，高级工程师，硕士，主要从事发电厂土建结构设计研究工作(e-mail)hexiyang@gedi.com.cn。

10.16516/j.gedi.issn2095-8676.2016.04.018

O342

A

2095-8676(2016)04-0088-04