电磁波反射折射能量守恒定律推导及应用

卢中昊， 尹家贤

(国防科技大学 电子科学与工程学院， 湖南 长沙 410073)

电磁波反射折射能量守恒定律推导及应用

卢中昊， 尹家贤

(国防科技大学 电子科学与工程学院， 湖南 长沙 410073)

电磁波在均匀分区媒质上发生折射和反射时的能量守恒定律一直是“电磁场理论”课程教学中一个缺乏充分论述且容易引起概念混淆的知识点。本文讨论了电磁波斜入射情况下的能量守恒问题，从功率的角度推导了能量守恒关系式，并介绍了天线罩增益损失的分析方法，这有助于学生直观理解和正确应用电磁波反射折射中的能量守恒定律。

电磁场理论；能量守恒定律；天线罩

0 引言

在本科“电磁场理论”课程的教学中，讲授电磁波在分区均匀媒质交界面上传播能量守恒定律时，大多数的教材讨论了入射波、反射波和透射波功率之间的关系，所定义的分界面的功率反射系数和功率投射系数均以实际坡印廷矢量在分界面的法向上的投影为参考，得到的结论是分界面上入射、反射、透射波的平均功率密度满足能量守恒关系[1,2]。这个结论当然毋庸置疑，但大多数学生对此容易产生概念混淆，入射波、反射波和透射波有各自的传播方向，自然，各自的坡印廷矢量方向与传播方向一致，也是各不相同，为什么在讨论能量守恒关系时一定要用各自在分界面法向的投影来考虑？如果不用投影，是不是就不能保持能量守恒关系？此外，几乎没有一本教科书就该部分理论的实际工程应用进行过举例，使得学生弄不清楚学习该部分知识的目的。为了解决这一问题，本文以平面波为例，从功率的角度对守恒定律重新进行推导，并进一步将该理论推广到分析天线罩增益损失的实际工程应用上。

1 理论基础

如图1所示，两种半无限大的媒质交界面为z=0平面，媒质参数分别为ε1、μ1和ε2、μ2。设入射波的入射角为θi，反射波的反射角为θr，透射波的透射角为θt，则入射波、反射波和透射波传播方向的单位矢量分别为

(1)

(2)

(3)

根据反射定律和斯涅尔定律(Snell′sLaw)，有

(4)

图1 电磁波在均匀媒质交界面上传播示意图

假设入射波为垂直极化波，此时入射波电场只有y方向分量，即

(5)

式中，E0是入射电场的幅度。根据菲涅尔公式，垂直极化波的反射系数Γ⊥和透射系数T⊥为

(6)

(7)

式中η1和η2分别是媒质1和媒质2的固有波阻抗。由反射系数和透射系数我们得到反射波和透射波的电场为

(8)

(9)

根据坡印廷定理和平面波中电场、磁场及传播常数三者之间的关系，我们得到入射波、反射波和透射波的坡印廷矢量为

(10)

(11)

(12)

从总的数值来说

(13)

因此，入射波的功率密度并不等于反射波和透射波的功率密度之和。

在z方向，入射波、反射波和透射波的功率密度分别为

(14)

(15)

(16)

这时，z方向的反射波和透射波能流密度之和为

(17)

所以有

(18)

式(18)就是z方向功率密度守恒的结论。

2 能量守恒定律的新推导

上一节从功率密度的角度推导了能量守恒定律，该方法也是大部分教材采用的推导方法。事实上，这一推导方法极易误导学生，让学生直观地产生错误理解，认为能量仅在z方向守恒，而在其他方向不守恒。为了消除这一误解，必须从功率的角度对能量守恒定律进行推导。

图2 电磁波在均匀媒质交界面上能量传输

为了方便理解，借鉴能流管的形式[3-5]，将入射波、反射波和折射波想象成在管道内均匀流动，在分界面上取一面积A，当入射波投射到这块面积的功率等于反射波从这块面积的反射功率和透射波从这块面积透射出去的功率之和时，可认为满足能量守恒定律。

下面进行具体证明，由功率和功率密度的关系可知，入射波、反射波和透射波投射到这块面积的功率分别为

(19)

(20)

(21)

式中，A1是入射波能量管的横截面积，A2是透射波能量管的横截面积。将式(10)-(12)代入式(19)-(21)，并令M=|E0|2/2，N=1/(η2cosθi+η1cosθt)2，则有

(22)

(23)

(24)

令P=Pr+Pt，代入式(23)和式(24)，则有

(25)

式(25)证明了入射波投射到这块面积的功率等于这块面积上反射波和透射波的功率之和，即满足了能量守恒定律。通过这个推导方法，使学生能够直观准确地把握能量守恒定律。

3 能量守恒关系的工程应用案例

大部分教科书都没有结合实际工程应用来说明学习能量守恒定律的目的，本节以天线罩的增益损失分析应用为例，来说明能量守恒定律相关知识是如何应用到科研工作中的。天线罩的结构如图3(a)所示。

(b)等效电路图3 夹层天线罩

天线罩的反射会引起传输损耗，从而影响天线增益。假设所有材料为无耗材料，根据相位匹配原理，平面波透过天线罩后的透射角与平面波从空气中的入射角是相同的，假设入射波的电场幅度为E0，入射角为θ0，反射系数为Γ，透射系数为T，可分别得出投影到入射区域面上的入射功率密度、反射功率密度和透射功率密度分别为

(26)

(27)

(28)

由能量守恒定律有

Si=Sr+St

(29)

由此可得

(30)

最后可得入射波与透射波的功率密度之比为

(31)

于是，可以计算出天线罩的增益损失(分贝数表示)：

(32)

从上述推导可以看出，增益损失最终由反射系数决定。为了快速简便求取反射系数，可将电磁波通过天线罩辐射等效为如图3(b)所示的传输线模型，即把特定坐标系下，以波矢量为特征的平面波投射到交界面时，与z垂直的横向电场、磁场沿z轴的传播与级联传输线上电压、电流波的传播等效。因此可求得各分界面上的输入阻抗如下：

(34)

(35)

(36)

式中，Zci(i=1,2,3):天线罩各层媒质的特性阻抗，βi=(i=1,2,3):天线罩各层媒质的传播常数，li(i=1,2,3)：天线罩各层媒质的厚度。于是，反射系数Γ最终可表达为

(37)

假设天线罩各层材料的参数如表2所示，图4为平面波入射角为30°平面波透过天线罩的功率密度损失。功率损失密度与入射角和频率均有关系，

天线罩存在最佳的透波频率点，当平面波斜入射时，若保持最佳的的透波频率点不变，这时天线罩要加厚，这与天线罩的分析是一致的。

表2 天线罩参数

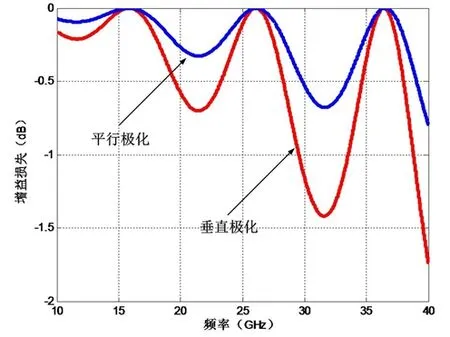
图4 平面波透过天线罩的功率损失

4 结语

本文从功率的角度直观地推导了电磁波在均匀分区媒质上传播能量守恒定律，得到了能量守恒关系式，有助于学生深入能量守恒关系的本质。利用能量守恒关系分析天线罩的增益损失，使学生能够明白知识点在实际工程中的应用，由此能够灵活运用能量守恒关系。

[1] 毛钧杰, 刘荧, 朱建清. 电磁场与微波工程基础[M],北京:电子工业出版社, 2004

[2] 钟顺时. 电磁场基础[M], 北京:清华大学出版社, 2006

[3] 郭琳, 张明, 洪伟. 电磁场教学中的电磁波斜入射问题讨论[J], 南京:电气电子教学学报, 1999, 21(4):22-24

[4] 杜晓燕, 杨明珊, 安娜． 关于坡印廷矢量教学的几点思考[J], 南京:电气电子教学学报, 2012, 34(6):118-120

[5] 张建华, 黄治. 电磁波反射折射中能量守恒关系的分析[J], 南京:电气电子教学学报, 2014, 36(1):31-34

The Derivation and Application of Energy Conservation Law in Electromagnetic Wave Reflection and Refraction

LU Zhong-hao, YIN Jia-xian

(CollegeofElectronicScienceandEngineering,NationalUniversityofDefenseTechnology,Changsha410073,China)

The law of energy conservation of electromagnetic wave refraction and reflection in the uniform partition medium is a easily confused knowledge point which has been a lack of adequate instructions in Electromagnetic Field Theory course. In this paper, the problem of energy conservation in the condition of electromagnetic wave oblique incident is discussed, energy conservation equation is deduced from the aspects of power, and the analysis method of the radome gain loss is introduced. All of these can help students intuitive understanding and correct application of the energy conservation law of the electromagnetic wave reflection and refraction.

electromagnetic field theory; law of energy conservation; antenna cover

2015-05-22;

2015-11- 16

卢中昊(1983-)，男，博士，讲师，主要从事电磁场与微波技术教学工作，E-mail：luzhnudt@163.com

G643

A

1008-0686(2016)02-0056-04