基于改进粒子群算法的阵列天线方向图综合设计
2016-12-29曹卫平张惠敏
曹卫平,杨 昭,张惠敏
(1.桂林电子科技大学 信息与通信学院,广西 桂林 541004;2.桂林电子科技大学 认知无线电与信息处理重点实验室,广西 桂林 541004)
基于改进粒子群算法的阵列天线方向图综合设计
曹卫平1,2,杨 昭1,张惠敏1
(1.桂林电子科技大学 信息与通信学院,广西 桂林 541004;2.桂林电子科技大学 认知无线电与信息处理重点实验室,广西 桂林 541004)
为了改善粒子群算法的优化性能,解决阵列天线波束赋形关于离散的优化问题处理不佳、容易陷入局部最优的问题,提出了一种新型的粒子群算法。该算法基于基本粒子群算法,引入控制因子和遗传算法的交叉变异机制,并应用于八单元偶极子圆环阵列天线。仿真结果表明,新型粒子群算法收敛速度快、精度高。
粒子群算法;阵列天线;方向图综合;交叉变异
随着通信技术的发展,智能优化算法在复杂设计领域、复杂目标函数及全局优化和实用性等方面显示出特有的优势。1995年,Kennedy等[1]提出了粒子群算法,该算法受到鸟类捕食的启发,通过群体建立模型、分析并模仿进而运用于实际问题。基本粒子群算法规则简单、实现容易、精度高、收敛快,但对于离散的优化问题处理不佳,在搜索过程的后期容易陷入局部最优,出现早熟现象,使优化精度大大降低。近年来,模糊PSO算法[2]、惯性权重模型[3]、自适应粒子群算法[4]等多种改进的粒子群算法被提出。Jin等[5]利用粒子群算法研究了线性阵列优化综合问题,Perez等[6]在远场阵列方向图可重构中应用粒子群算法进行研究,提高了收敛精度。为了满足实际要求,设计了天线的激励幅度、相位等参数,以实现不同的波束方向图[7]。为避免算法过早收敛,对基本粒子群算法引入遗传算法的交叉、变异机制[8]改善算法的优化性能,并采用改进的粒子群算法对八单元偶极子圆环阵列天线方向图进行综合设计。
1 基本粒子群算法
基本粒子群算法的搜索空间中,每个优化问题的解为“粒子”。每个粒子由优化适应函数决定其适应值,且粒子的速度决定其飞行的方向和距离。算法首先初始化一个粒子群(粒子数为d),并给定随机的速度和位置使其在搜索空间中飞行,并通过迭代搜索最优解。每次迭代均有新的个体最优位置P=(p1,p2,…,pd)和群体最优位置G=(g1,g2,…,gd)并不断进行更新,直至得到满足要求的适应值或者达到预设的最大迭代次数。个体最优即粒子本身的最优解,群体最优即整个种群的最优解。通过粒子群算法,粒子i的更新速度和位置为:
(2)

2 改进粒子群算法
2.1 引入控制因子
通过基本粒子群算法更新粒子位置时,粒子经常超出规定的速度边界(一般基本粒子群算法限定的速度范围为[-0.6,0.6])。当粒子跃过限定的最大速度vmax或者最小速度vmin时,引入控制因子Ki调节粒子飞行速度,将跃出边界的粒子拉进限定的范围。其中,控制因子
(3)
调控后的粒子速度
(4)
2.2 交叉操作
交叉是结合父代交配种群中的信息产生新的个体,首先,限定粒子位置处于位置边界当中(一般基本粒子群算法限定的位置范围为[-1,1])。当粒子的位置超出最大边界xmax时,限定该粒子的位置为边界最大值;当粒子的位置超出最小边界xmin时,限定该粒子的位置为边界最小值。其次,寻找交叉点C。若r 图1 交叉操作Fig.1 Crossover 2.3 变异操作 y=xmin+(xmax-xmin)×r。 (5) 为了说明改进后的粒子群算法的有效性和优势,采用八单元偶极子圆环阵列天线方向图综合进行分析验证。运用改进前后的粒子群算法分别对阵列天线进行赋形。首先提取天线阵列中每个单元的远场方向图数据作为初始数据,阵元作为理想点源。综合八单元偶极子圆环阵列天线,对俯仰面进行波束赋形,要求主波束指向为90°,3 dB波束宽度不小于25°,工作频率为4.4 GHz。以每个单元的幅度和相位作为优化权值,并与CST仿真结果进行对比,如图2所示。从图2可看出,改进粒子群算法得到的方向图,与CST仿真结果几乎一致,曲线相似度很高,但应用基本粒子群算法进行综合得到的方向图与CST仿真结果相差较大。改进粒子群算法的主波束指向为89°,3 dB波束宽度为36.5°,增益为14.7 dBi,其收敛速度更快,满足设计要求。 图2 改进粒子群算法、粒子群算法和CST仿真结果Fig.2 Simulation results of the improved PSO, PSO and CST 圆环阵列天线如图3所示。实测结果与CST仿真结果如图4所示。 图3 圆环阵列Fig.3 Circle array 图4 实测结果与CST仿真结果Fig.4 Measured result and CST simulation result 从图4可看出,采用改进粒子群算法的优化值应用到阵列天线中,得到的结果与电磁仿真软件CST的仿真结果几乎一致,满足了设计要求。 粒子群算法作为一种新兴的优化算法,由于理论简单、精度高、收敛快而被广泛应用,但基本粒子群算法对离散的优化问题处理不佳,容易陷入局部最优,从而产生早熟现象。在基本粒子群算法基础上加入控制因子和遗传算法的交叉变异机制,打乱粒子的初始轨迹,降低了粒子聚集的可能性,较好地解决了早熟的问题。通过对双层圆环阵列的仿真,证明了改进的粒子群算法的有效性。改进的粒子群算法适用于其他阵列天线方向图综合,具有很强的实用性。 [1] KENNEDY J,EBERHART R C.Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks,1995:1942-1948. [2] SHI Y,EBERHART R C.Fuzzy adaptive particle swarm optimization[C]//Proceedings of the 2001 Congress on Evolutionary Computation.Seoul:IEEE,2001:101-106. [3] SHI Y, EBERHART R.A modified particle swarm optimizer[C]//Proceedings of IEEE World Congress on Computational Intelligence, IEEE International Conference on Evolutionary Computation,1998: 69-73. [4] YASUDA K, IWASAKI N.Adaptive particle swarm optimization using velocity information of swarm[C]//IEEE International Conference on Systems, Man and Cybernetics,2004:516-520. [5] JIN N,RAHMAT-SAMII Y.Advances in particle swarm optimization for antenna designs:real-number,binary, single-objective and multi-objective implementations[J].IEEE Transactions on Antennas and Propagation,2007,55(3):556-567. [6] PEREZ J R,BASTERRECHEA J.Particle swarm optimization for antenna far-field radiation pattern reconstruction[C]//36th European Microwave Conference.Manchester:IEEE,2006:687-690. [7] HAMMAMI A,GHAYOULA R,GHARSALLAH A.Antenna array synthesis with Chebyshev-Genetic algorithm method[C]//IEEE International Conference on Communications, Computing and Control Applications,2011:1-4. [8] RIDWAN M,ABDO M,JORSWIECK E.Design of non-uniform antenna arrays using genetic algorithm[C]//13th IEEE International Conference on Advanced Communication Technology,2011:422-427. [9] ROBINSON J,SINTON S,RAHMAT-SAMII Y.Particle swarm,genetic algorithm,and their hybrids:optimization of a profiled corrugated horn antenna[C]//IEEE Antennas and Propagation Society International Symposium,2002:314-317. 编辑:曹寿平 Design of array antenna beam pattern synthesis based on improved particle swarm optimization CAO Weiping1,2, YANG Zhao1, ZHANG Huimin1 (1.School of Information and Communication Engineering, Guilin University of Electronic Technology, Guilin 541004, China;2.Key Laboratory of Cognitive Radio and Information Processing,Guilin University of Electronic Technology, Guilin 541004, China) In order to improve the performance of particle swarm optimization and solve the problem that an array antenna beamforming optimization may not meet the requirement but lead to local optimum, a new particle swarm optimization is proposed. On the basis of conventional particle swarm optimization, control factors and crossover and mutation mechanism of genetic algorithm are introduced and applied for 8 elements ring dipole array antenna. The simulation results show that the new particle swarm optimization converges fast, its precision is high as well. particle swarm optimization; array antenna; pattern synthesis; crossover and mutation 2016-03-08 国家自然科学基金(61361005,61001020,61461016);桂林电子科技大学研究生教育创新计划(YJCXS201526) 曹卫平(1971-),男,湖南益阳人,教授,博士,研究方向为宽带电小天线、智能天线。E-mail:weipingc@guet.edu.cn 曹卫平,杨昭,张惠敏.基于改进粒子群算法的阵列天线方向图综合设计[J].桂林电子科技大学学报,2016,36(6):466-468. TN929.5 A 1673-808X(2016)06-0466-03
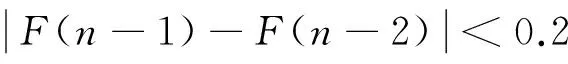
3 分析验证

4 阵列天线测试结果


5 结束语
