一类G1连续的空间五次PH曲线
2016-12-29彭丰富
彭丰富,刘 惠
(桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)
一类G1连续的空间五次PH曲线
彭丰富,刘 惠
(桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)
为了构造空间五次Pythagorean-hodograph G1连续曲线,对离散数据进行G1Hermite插值,给出一种基于空间PH曲线充分必要条件的构造方法。从曲线的导矢出发,比对四次导函数和五次Bézier曲线的四次导函数在Bernstein基下的系数,组成等式,并与五次Bézier曲线导函数在Bernstein基函数下的系数和曲线控制多边形顶点的关系组成方程组。通过求解方程组可构造出一段满足端点及其导矢方向条件且G1连续的PH曲线,并给出数值实例。此构造方法直观,有多个自由参数可对曲线进行形状控制。数值实验证明,对给定空间数据点插值效果较好。
PH空间曲线;G1Hermite插值;Bézier曲线;Bernstein基函数
1990年Farouki等首次提出了一类特殊的平面多项式曲线,简称为PH(Pythagorean-hodograph)曲线,开辟了有理表示精确研究的先河。这类曲线的一个突出特点是切线的模长为多项式,因此,这类曲线具有精确的有理等距曲线,且弧长为多项式。1994年Farouki等[1]定义并研究了空间PH曲线,平面与空间PH曲线的定义有完全不同的代数结构。在实际应用过程中,需要利用Hermite(简称H)插值,对已知有序离散点列的两端点位矢、单位切矢或有向曲率作插值来构造PH曲线。对于离散数据的插值,PH曲线往往产生比经典多项式曲线更光顺的轨迹曲线。因此,对PH曲线生成方法的研究成为一大热点。而相对于国外,国内对空间PH曲线的研究相对较少。2002年李胜军[2]研究了平面三次PH曲线G1H插值问题的算法,得出四次PH曲线的一阶H插值的解,给出构成五次PH曲线的充要条件,分析其控制多边形的几何意义,并利用空间三次PH曲线构造扫曲面和管道面。同年Farouki等[3]给出空间五次PH曲线的C1H插值算法。2005年PELOSI等[4]提出了空间三次PH曲线的G1连续插值算法。而Juttler[5-6]从几何角度分别给出了空间分段三次PH曲线G1连续插值算法与平面七次PH曲线的G2H插值算法,该方法适合于逼近能够计算出切向、曲率的非PH曲线。2008年Kim等[7]研究了一些由平面到空间的多项式(或有理)映射,此映射保留了毕达哥拉斯矢端曲线的性质,即将PH曲线映射到PH曲线,并定义了升阶PH保留映射。因此,可以应用已知的平面PH多项式曲线的C1H数据和一些合适的升阶PH保留映射,解决空间PH多项式曲线的C1H插值问题。FAROUKI等[8]分析了空间PH三次Hermite插值问题,并给出解存在的充要条件,以四元数模型为基础,用一种比在以前场合下更几何的形式,介绍了空间PH五次Hermite插值问题。同时分析了空间五次PH曲线的弧长,给出选择PH五次Hermite插值的2个自由参数的4个标准。2014年Huard等[9]研究从离散的传感器数据中重建空间曲线,提供了2种C2PH五次样条插值方法,这2种方法都服从每个样条段有规定弧长的限制进行插值,第一种方法是关于一系列点的插值,第二种方法主要是针对导数的插值。
为此,基于空间PH曲线的充要条件,用G1H插值对离散的已知型值点列及其端点位矢构造G1连续的空间五次PH曲线,给出了另一种五次PH曲线的生成方法,并给出了应用实例。
1 空间PH曲线
r(t)为空间Pythagorean-hodograph曲线,其定义为:对一条空间多项式参数曲线
r(t)=(x(t),y(t),z(t))T,
(1)
存在一个多项式σ(t),使得
x′2(t)+y′2(t)+z′2(t)=σ2(t)。
(2)
定理1[9]空间参数曲线式(1)为PH曲线,当且仅当存在4个多项式u(t)、v(t)、p(t)、q(t),使
(3)
以及参数速度
σ(t)=u2(t)+v2(t)+p2(t)+q2(t),
(4)
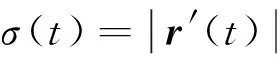
2 空间PH曲线的生成
因PH曲线为多项式曲线,可改写成以Bernstein基函数为基的Bézier形式,则对于空间PH曲线,只需确定其空间控制多边形顶点,即可生成所需曲线。如何构造基于PH曲线充要条件满足初始条件的空间五次PH曲线为研究的关键。
设空间五次Bézier曲线为
(5)
其中:pi(i=0,1,…,5)为空间曲线控制多边形顶点;B5,i(t)(i=0,1,…,5)为五次Bernstein基函数。对式(5)求导,
记
此时,对一组给定的型值点,若能确定a、b、c、d、e的值,则可生成空间五次PH曲线:
对于空间五次PH曲线,定理1中的4个多项式u(t)、v(t)、p(t)、q(t)均为二次的,分别设其为二次Bézier形式:
(8)
其中ai、bi、ci、di(i=0,1,2)均为未知参数。将式(8)代入式(3)组成空间五次PH曲线的导函数向量r′(t),并进行形式整理。使Bézier形式导函数式(6)与此导函数向量相等,分别比较B4,i(t) , i=0,1,2,3,4,五个Bernstein基函数的向量型系数可得方程组:
(9)
其中:
此时方程组(9)并不一定有解。
现对空间任意已知两型值点Pi、Pj及其切矢方向Ti、Tj进行G1H插值,构造一段空间五次PH曲线。取p0=Pi,m1=Ti+p0,p5=Pj,m4=Tj+p5均为已知量,令
(10)
其中α、β、ω为自由参数,可以先给定或作为形状控制因子,λ1、λ2、λ3为未知参数。将式(9)与式(10)联合组成新的方程组,共组成15个标量方程组,解出λ1、λ2、λ3及ai、bi、ci、di(i=0,1,2)在内的15个未知参数。则可生成一条满足端点及其导矢方向的空间五次PH曲线。曲线生成方法算法:
1)输入有序点Pi、Pj,对应的导矢Ti、Tj,形状控制因子α、β、ω及矩阵 Mi(i=1,2,3,4,5);
2)计算p0=Pi,m1=Ti+p0,p5=Pj,m4=Tj+p5,a=αTi,e=βTj及ω(m4-p1);
3)由式(9)与式(10)合并组成方程组,并求解方程组2),解出λ1、λ2、λ3的解;
4)由式(10)输出a、b、c、d的值;
5)生成空间五次PH曲线的表达式(7)。
3 数值实例
从球面上的一条曲线r=(x,y,z)Τ上取7个点,并给定7个点及其导矢如表1和图1所示。
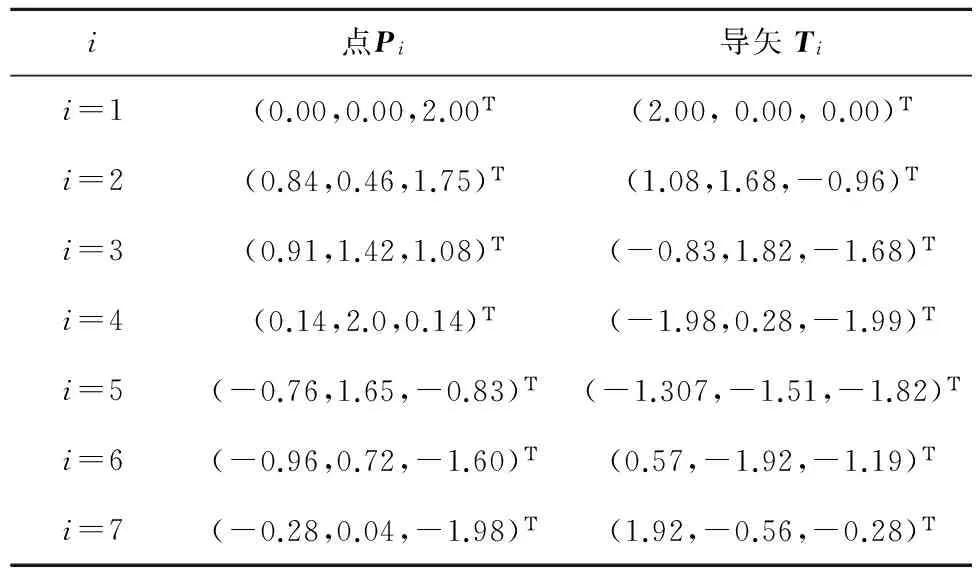
表1 7个点的数据
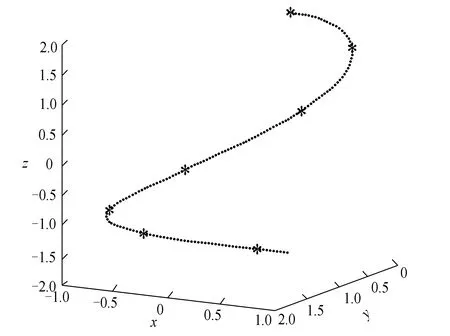
图1 球面所取空间曲线Fig.1 Spatial curve from a spherical surface
对这7个有序点列进行逐段C1连续G1H插值构造空间五次PH曲线,如图2所示。

图2 空间五次PH曲线Fig.2 Spatial quintic PH curve
实例中自由选取的3个自由参数α、β、ω,对第一段2个点插值取α=0.25、ω=-0.05、β=0.05,对于此后的各点段插值均取α=0.05、ω=0.15、β=0.05。这样保证了整个曲线不仅是G1连续,更是C1连续的。
4 结束语
对于离散的有序型值点列及其导矢,给出了经过已知离散点列,且G1连续的空间五次PH曲线的一种构造方法。此方法是在保证空间PH曲线充要条件的基础上,研究空间五次多项式曲线导函数在Bézier形式下的Bernstein基函数的向量型系数满足的条件,以及系数与曲线控制点之间的关系,通过组成方程组进行求解,带有几个可自由变动的参数可以控制曲线形状。今后的工作可以运用此方法对离散数据进行拟合,也可加上弧长作为约束条件,或许会有不一样的效果,并可进一步研究空间PH曲线的性质。
[1] FAROUKI R T,SAKKALIS T.Pythagorean-hodograph space[J].Advances in Computational Mathematics,1994,2:41-66.
[2] 李胜军.PH曲线的研究及其应用[D].西安:西北工业大学,2002.
[3] FAROUKI R T,KANDARI M A,SAKKALIS T.Hermite interpolation by rotation-invariant spatial Pythagorean-Hodograph curves[J].Advnaces in Computational Mathematics,2002,17(4):369-383.
[4] PELOSI F,FAROUKI R T,MANNI C,et al.Geometric Hermite interpolation by spatial Pythagorean-Hodograph cubics[J].Advnaces in Computational Mathematics,2005,22(4):325-352.
[5] JUTTLER B,MAURER C.Cubic Pythagorean Hodograph spline cuvres and applications to sweep surface modeling [J].Computer Aided Design,1999,31(1):73-83.
[6] JUTTLER B.Hermite interpolation by Pythagorean Hodograph curves of degree seven[J].Mathematics of Computation,2000,70(235):1089-1111.
[7] KIM G I,LEE S.Pythagorean-hodograph preserving mappings[J].Journal of Computational and Applied Mathematics,2008,216(1):217-226.
[8] FAROUKI R T,GIANNELLI C,MANNI C,et al.Identification of spatial PH quintic Hermite interpolants with near-optimal shape measures[J].Computer Aided Geometric Design,2008,25(4-5):274-297.
[9] HUARD M,FAROUKI R T,SPRYNSKI N,et al.C2interpolation of spatial data subject to arc-length constraints using Pythagorean-hodograph quintic splines[J].Graphical Models,2014,76(1):30-42.
编辑:梁王欢
A G1-continuity spatial quintic PH curve
PENG Fengfu, LIU Hui
(School of Mathematics and Computing Science, Guilin University of Electronic Technology, Guilin 541004, China)
To construct G1continuity spatial quintic Pythagorean-hodograph curve. Interpolating given spatial discrete data with G1Hermite,a method,based on the sufficient and necessary conditions of PH space curve,is given. Starting from the derived vectors of a curve,we compare with the vector coefficients of the front quartic derived functions and the quartic derived vector of a quintic Bézier space curve under Bernstein basis to compose a system of equations,then compose a bigger system of equations with the relationships of the coefficients of the latter quartic derived function under Bernstein basis with the points of curve’s control polygon . Next solving these equations,We can construct a G1continuity spatial quintic Pythagorean-hodograph curve,that satisfies the given endpoint and derived vector,according to G1Hermite interpolation,and a numerical example is presented. This construction method is intuitive,it includes multiple free parameters to control the shape of curve,and it works well to interpolate the space data points with some numerical experiments.
PH spatial curve; G1Hermite interpolation; Bézier curve; Bernstein basis function
2016-04-14
广西自然科学基金(2015GXNSFAA139014)
彭丰富(1972-),男,湖南双峰,副教授,博士,研究方向为计算机辅助几何设计。E-mail:pengfengfu@aliyun.com
彭丰富,刘惠.一类G1连续的空间五次PH曲线[J].桂林电子科技大学学报,2016,36(6):504-507.
TP391.7
A
1673-808X(2016)06-0504-04
