柔性二级倒立摆的准滑动模态控制研究

王 珏，谢慕君，李元春

(长春工业大学电气与电子工程学院，吉林 长春 130012)

柔性二级倒立摆的准滑动模态控制研究

王 珏，谢慕君，李元春

(长春工业大学电气与电子工程学院，吉林 长春 130012)

柔性二级倒立摆是一个高阶非线性强耦合的自然不稳定系统，为了对其进行稳摆控制，基于建模机理建立了柔性二级倒立摆数学模型，提出准滑动模态控制方法，设计了滑模变结构控制器，使系统具有较好的稳摆控制和鲁棒性.仿真结果表明：基于准滑动模态控制的滑模变结构控制方法能够更好地实现倒立摆稳定控制；比传统指数趋近率的滑模控制器输出更加平滑，削弱了抖振.

柔性二级倒立摆；滑模变结构；准滑动模态

0 引言

倒立摆系统具有非线性、强耦合、多变量等不稳定特性，从理论上涉及跟踪、非线性、鲁棒性、镇定等控制系统研究的关键问题，因此成为检验各种新的控制理论和方法的典型模型.柔性二级倒立摆系统是在直线二级倒立摆系统的基础上加入了自由弹簧系统，由于闭环系统受弹簧振荡频率的限制，对该系统进行稳摆控制变得更加复杂和困难.目前，针对柔性二级倒立摆稳摆控制主要有以下几种方法：LQR控制方法实现了柔性二级倒立摆的稳摆控制[1]，但摆杆存在抖动；传统滑模变结构控制方法实现了柔性二级倒立摆的稳摆控制[2]，但系统输入存在抖振，鲁棒性较差；基于BP神经网络的模糊控制方法实现了柔性二级倒立摆的稳摆控制[3]，但调节时间较长.上述控制方法均实现了柔性二级倒立摆的稳摆控制，但均存在不足.本文针对柔性二级倒立摆的稳摆控制，采用准滑动模态控制思想设计控制器，调节时间较短，降低控制器输出的抖动程度，提高柔性二级倒立摆系统的鲁棒性.

1 柔性二级倒立摆系统模型的建立

弹簧等不确定性因素的存在，使得柔性二级倒立摆的数学模型建立比较困难[4].但在忽略了摩擦、空气阻力后，可以把其抽象成由匀质摆杆、小车和弹簧组成的系统[5].本文采用机理建模法建立柔性二级倒立摆系统的数学模型，系统参数取自固高科技有限公司柔性倒立摆实验装置GLIP2013.该系统抽象的物理模型见图1.

图1 柔性二级倒立摆抽象物理模型

对一级摆杆水平方向的受力进行分析可得

(1)

对一级摆杆垂直方向的受力进行分析可得

(2)

一级摆杆力矩平衡方程为

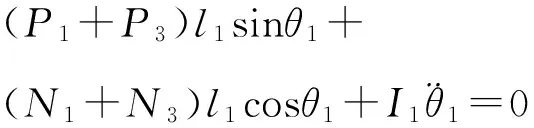
(3)

对质量块水平方向的受力进行分析可得

(4)

对质量块垂直方向的受力进行分析可得

(5)

对二级摆杆水平方向的受力进行分析可得

(6)

对二级摆杆垂直方向的受力进行分析可得

(7)

二级摆杆力矩平衡方程为

(8)

其中

设θ1=π+φ1，θ2=π+φ2(φ1与φ2分别是一级摆杆、二级摆杆与垂直向上方向的夹角)，并假设

φ1≪1 rad，φ2≪1 rad.

(9)

(10)

代入参数后得:

(11)

(12)

将从动小车、摆杆和质量块看做一个整体进行受力分析，可得

(13)

令

则传递函数转化为

(14)

则系统的状态空间方程为

(15)

其中：

由系统的状态空间方程可看出，柔性二级倒立摆系统是强耦合、高阶不稳定系统.针对该复杂系统的稳摆控制，设计如下控制器，使其不仅达到较好的稳摆控制效果且控制器输出抖动较小.

2 准滑动模态控制器的设计

在实际工程中，由于存在时间的延迟和空间上的滞后使得在滑模控制系统中滑动模态呈抖振形式[6].因此，本文采用准滑动模态控制系统.

所谓准滑动模态是指系统的运动轨迹被限制在理想滑动模态的某一Δ邻域内的模态.从相轨迹方面来说，就是使一定范围内的运动状态点均吸引至切换面的某一Δ邻域内，通常称该Δ邻域为滑动模态切换面的边界层[7].在边界层内，准滑动模态是不要求满足滑动模态的存在条件的.

该控制器设计的基本步骤包括切换函数s(x) 的设计和准滑动模态控制率u(x)的设计2个相对独立的部分.

2.1 切换函数的设计

切换函数[8]为

s=Zx.

(16)

采用Ackermann公式设计Z值为

Z=eTP(λ).

(17)

Ackermann公式为：

eT=[0，…，0，1][b，Ab，…，An-1b]-1；

(18)

P(λ)=(λ-λ1)(λ-λ2)…(λ-λn-1).

(19)

在二级柔性倒立摆系统中，当n=8，取λ1=-5，λ2，3=-50±0.7i，λ4，5=-25±2.7i，λ6，7=-35±2.7i，根据Ackermann公式设计Z值，可得Z=[225，1，-188.28，13.47，-4.61，-2.23，-32.15，-5.94].

2.2 准滑动模态控制率的设计

准滑动模态控制率为

(20)

其中

(20)式中Δ称为边界层.该控制率的实质是在边界层外，采用基于指数趋近率的切换控制，在边界层之内，采用线性反馈控制[9].

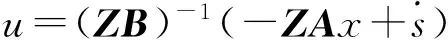
(21)

把(20)式带入(21)式得系统控制率

u=(ZB)-1(-ZAx-εs2sat(s)-ks).

(22)

3 仿真分析

图2 传统指数趋近率滑模控制主、从动小车的位移

图3 传统指数趋近率滑模控制一级摆杆、二级摆杆的角度

图4 传统指数趋近率滑模控制控制器的输出

从图2和3可以看出，基于传统指数趋近率的柔性二级倒立摆滑模控制位置跟踪速度比较快，图4的控制器的输出具有较强的抖振，因此增加了控制器的负担.

图5 准滑动模态控制主、从动小车的位移

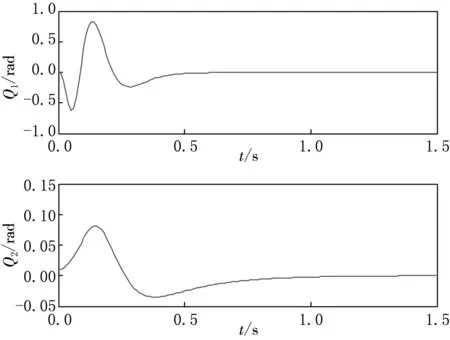
图6 准滑动模态控制一级摆杆、二级摆杆的角度

图7 准滑动模态控制控制器的输出

从图5和6可以看出，准滑动模态控制的柔性二级倒立摆保证了位置跟踪速度，图7的控制器输出趋于平滑，因此有效地减弱了柔性二级倒立摆系统的抖动.由于基于传统指数趋近率的控制使一定范围内的状态点被吸引至切换面，准滑动模态控制使一定范围内的状态点被吸引至切换面的某一Δ邻域内，因此，在使用MATLAB进行仿真的过程中，从开始运行到得到仿真结果，准滑动模态控制使用时间在1 s左右，传统指数趋近率的滑模控制使用时间在10 s左右，提高了运行效率.

4 结束语

本文针对柔性二级倒立摆的稳摆控制，设计了准滑动模态滑模控制器，通过MATLAB仿真实验验证了此控制器对于该系统的有效性.从仿真曲线可以看出，系统在0.9 s内迅速达到稳定，相对比基于传统指数趋近率的滑模控制，准滑动模态滑模控制抑制了控制器的输出抖动，鲁棒性更优.

[1] 吴昊，秦志强，朱学峰，等.直线柔性连接两级倒立摆控制器设计[J].控制工程，2003，10(6):497-499.

[2] 姜峰.直线二级柔性倒立摆的滑模变结构控制仿真研究[J].科技向导，2013(3):81-82.

[3] YU JIMIN，HUANG LINYAN. Fuzzy control of linear flexible double inverted pendulum sustem [C]// 2012 International Conference on Control Engineering and Communication Technology，Washington：IEEE Computer Society，2012:342-345.

[4] ANIRBAN BANREJEE，NIGAM M J. Designing of proportional sliding mode controller for linear one stage inverted pendulum [J].Power Engineering and Electrical Engineering，2011(9):84-89.

[5] PUNITKUMAR BHAVSAR，VIJAY KUMAR. Trajectory tracking of linear inverted pendulum using integral sliding mode control [J]. Intelligent Systems and Applications，2012(6)：31-38.

[6] 刘金琨.滑模变结构控制MATLAB仿真[M].北京：清华大学出版社，2005：32-79.

[7] 高为炳.离散时间系统的变结构控制[J].自动化学报，1995，21(2):154-161.

[8] 谢慕君，王辉.模糊趋近率的滑模控制在倒立摆系统中的应用研究[J].自动化技术与应用，2008，27(10):8-11.

[9] 章仁华，马静.航空发动机准滑动模态变结构控制[J].计算机仿真，2011，28(1):103-106.

[10] 刘金琨，孙富春.滑模变结构控制理论及其算法研究与进展[J].控制理论与应用，2007，24(3):407-418.

(责任编辑：石绍庆)

Research on the control of flexible double inverted pendulum system based on quasi-sliding-mode control

WANG Jue，XIE Mu-jun，LI Yuan-chun

(Institute of Electrical and Electronic Engineering，Changchun University of Technology，Changchun 130012，China)

Flexible double inverted pendulum system is a higher order，nonlinear and strong coupling unstable system. In order to steady the pendulum，a mathematical model based on mechanism modeling method is established，and quasi sliding mode control method is put forward，then the sliding mode controller is designed. And then the system has good stability control and robustness. The simulation results show that，the quasi sliding mode control can realize stable control of inverted pendulum，and it is more smooth than general sliding mode control based on exponent trending law in system input，and reducing the shake of the system.

flexible double inverted pendulum system；sliding mode control；quasi sliding mode

1000-1832(2016)04-0083-05

10.16163/j.cnki.22-1123/n.2016.04.018

2015-06-09

国家自然科学基金资助项目(61374051).

王珏(1990—)，女，硕士研究生；通讯作者：谢慕君(1969—)，女，博士，教授，主要从事智能机械与机器人技术和现代节能技术研究.

TP 273 [学科代码] 510·80

A