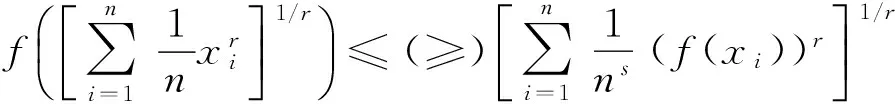r次幂平均s-凸函数及其Jensen型不等式
2016-12-29宋振云陈少元胡付高
宋振云,陈少元,胡付高
(1.湖北职业技术学院机电工程学院,湖北 孝感 432000;2.湖北职业技术学院教务处,湖北 孝感 432000;3.湖北工程学院数学与统计学院,湖北 孝感 432100)
r次幂平均s-凸函数及其Jensen型不等式
宋振云1,陈少元2,胡付高3
(1.湖北职业技术学院机电工程学院,湖北 孝感 432000;2.湖北职业技术学院教务处,湖北 孝感 432000;3.湖北工程学院数学与统计学院,湖北 孝感 432100)
考虑了函数的凸性及其广义凸性,提出并研究了r次幂平均s-凸函数,讨论了它的若干判定定理及运算性质,建立了其Jensen型不等式,并给出了Jensen型不等式的等价形式及推论.研究结果表明,r次幂平均s-凸函数是算术凸函数(凸函数)、几何凸函数、调和凸函数、平方凸函数、调和平方凸函数以及r-平均凸函数的推广,为研究新的凸函数和推广拓展凸函数概念探索了一条新途径.
s-凸函数;r次幂平均s-凸函数;判定定理;Jensen型不等式.
0 引言
凸函数是应用十分广泛的一类重要函数,其不可替代的作用已是我们大家所熟知的.因此,以凸集和凸函数为主要内容的凸分析便成为近年来数学研究中一个十分活跃的研究领域,特别是以实函数有意义的连续区间上任意两点的幂平均函数值与其对应点函数值的同一幂平均值的大小比较而确定的经典凸函数概念随着研究的深入被不断推陈出新.目前,采用此类方法建立的凸函数,先后被提出的有算术凸函数(凸函数)、几何凸函数[1]、调和凸函数[2]、平方凸函数[3]、调和平方凸函数[4]、r-平均凸函数[5]等.也有以实函数有意义的连续区间上任意两点的幂平均函数值与其对应点函数值的不同幂平均值的大小比较而确定的凸函数概念,如指数凸函数(GA-凸函数[6])、GH-凸函数[7]及其推广GM-凸函数[8]等,又如对数凸函数[9](AG-凸函数)、AH-凸函数[10]及其推广AM-凸函数[11]等.然而,换一个角度思考,则会发生新的变化.1985年,文献[12]给出了Godunova-Levin函数定义:
定义1 设f(x)是定义在区间I⊆R上的非负值函数.若∀x1,x2∈I及∀λ∈(0,1),有

(1)
则称f(x)是Godunova-Levin函数,或称f(x)属于Q(I)函数类.
定义2[13]设s∈(0,1],f:R→R.若∀x1,x2∈R及∀λ∈[0,1],有
f(λx1+(1-λ)x2)≤λsf(x1)+(1-λ)sf(x2),
(2)

在此后的研究中,许多专家学者以s-凸函数为主要对象进行了卓有成效的研究,尤其是对s-凸函数的Hermite-Hadamard型不等式的探索取得了丰硕成果.[14-19]本文受此启发,提出了r次幂平均s-凸函数的概念,通过对r次幂平均s-凸函数的系统研究,给出了r次幂平均s-凸函数的若干判定定理和运算性质,建立了r次幂平均s-凸函数的Jensen型不等式.
定义3 设I⊆R+,s∈(0,1],f:I→R+.若∀x1,x2∈I及∀t∈[0,1],存在r∈R,使得
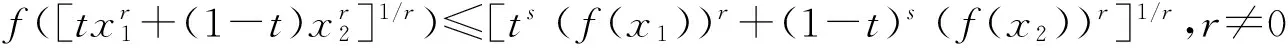
(3)

(4)
则称f(x)为I上的r次幂平均s-凸函数. 若上述不等号反向,则称f(x)为I上的r次幂平均s-凹函数.
显然,当s=1且r分别等于1,0,-1,2,-2及r∈R时,r次幂平均s-凸函数即分别为凸函数、几何凸函数、调和凸函数、平方凸函数、调和平方凸函数和r-平均凸函数.
1 r次幂平均s-凸函数的判定及性质
本文约定所有讨论只考虑r≠0的情况,关于r=0时的相关问题将另文讨论.因为区间I⊆R+上的实值函数μ(x)=xr当r≠0时是单调的,因此记μ(I)=Ir.
定理1 设I⊆R+,s∈(0,1],f:I→R+,则:
(ⅰ) 当r>0时,f为I上的r次幂平均s-凸(凹)函数的充要条件是(f(x1/r))r为Ir上的s-凸(凹)函数;
(ⅱ) 当r<0时,f为I上的r次幂平均s-凸(凹)函数的充要条件是(f(x1/r))r为Ir上的s-凹(凸)函数.
证明 仅证(ⅰ),同理可证 (ⅱ).设g(x)=(f(x1/r))r(x∈Ir,且r>0).
充分性.如果g(x)=(f(x1/r))r为Ir上的s-凸函数,且r>0,那么∀x1,x2∈I及∀t∈[0,1],有
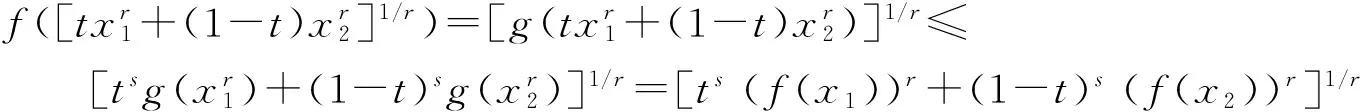
故f为I上的r次幂平均s-凸函数.
必要性.如果f为I上的r次幂平均s-凸函数,r>0,那么∀x1,x2∈Ir及∀t∈[0,1],则有

因此g(x)=(f(x1/r))r是Ir上的s-凸函数.
若f在I上是s-凹函数,则上述证明中的不等号反向,所以定理1(ⅰ)的后半部分成立.
定理2 设I⊆R+,s∈(0,1],f:I→R+,则:


证明 仅证(ⅰ),同理可证 (ⅱ).
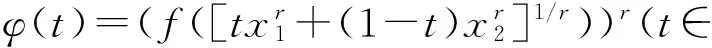
充分性.若φ(t)是[0,1]上的s-凸函数,则

注意到r>0,且f是I上的正值函数,所以

从而f为I上的r次幂平均s-凸函数.
必要性. ∀x1,x2∈I及∀t1,t2∈[0,1],根据正数的幂平均性质[20]有




若φ(t)在[0,1]上是s-凹函数,并注意到r>0,则上述证明中的不等号反向,故定理2(ⅰ)的后半部分亦成立.
定理3 设I⊆R+,s∈(0,1],f:I→R+,则:
(ⅰ) 当r>0时,f为I上的r次幂平均s-凸(凹)函数的充要条件是∀x1,x2,x3∈I,x1 (ⅱ) 当r<0时,f为I上的r次幂平均s-凸(凹)函数的充要条件是∀x1,x2,x3∈I,x1 证明 仅证(ⅰ),同理可证 (ⅱ). 如果f为I上的r次幂平均s-凹函数,并注意到r>0,则上述证明中的不等号反向,所以定理3(ⅰ)的后半部分成立. 定理4 设I⊆R+,s∈(0,1],f:I→R+,f是I上二阶可导函数,且r>0. (ⅰ) 若∀x∈I,xf(x)f″(x)+(r-1)x(f′(x))2+(1-r)f(x)f′(x)≥0,则f(x)为I上的r次幂平均s-凸函数; (ⅱ) 若f(x)为I上的r次幂平均s-凹函数,则∀x∈I, xf(x)f″(x)+(r-1)x(f′(x))2+(1-r)f(x)f′(x)≤0. t(f(x1))r+(1-t)(f(x2))r≤ts(f(x1))r+(1-t)s(f(x2))r, [t(f(x1))r+(1-t)(f(x2))r]1/r≤[ts(f(x1))r+(1-t)s(f(x2))r]1/r. (ⅱ) 若f(x)为I上的r次幂平均s-凹函数,且r>0,则 所以f(x)是I上的r-平均凹函数,即 ∀x∈I,xf(x)f″(x)+(r-1)x(f′(x))2+(1-r)f(x)f′(x)≤0(r>0). 类似地有如下结论. 定理5 设I⊆R+,s∈(0,1],f:I→R+,f是I上二阶可导函数,且r<0. (ⅰ) 若∀x∈I,xf(x)f″(x)+(r-1)x(f′(x))2+(1-r)f(x)f′(x)≤0,则f(x)为I上的r次幂平均s-凹函数; (ⅱ) 若f(x)为I上的r次幂平均s-凸函数,则∀x∈I有 xf(x)f″(x)+(r-1)x(f′(x))2+(1-r)f(x)f′(x)≥0. 定理6 设A,I⊆R+,s∈(0,1],f:I→R+,μ:A→B⊆I,则: (ⅰ) 若y=f(u)是I上严格递增的r次幂平均s-凸函数,u=μ(x)是A上的r-平均凸函数,则y=f(μ(x))是A上的r次幂平均s-凸函数; (ⅱ) 若y=f(u)是I上严格递减的r次幂平均s-凸函数,u=μ(x)是A上的r-平均凹函数,则y=f(μ(x))是A上的r次幂平均s-凸函数; (ⅲ) 若y=f(u)是I上严格递增的r次幂平均s-凹函数,u=μ(x)是A上的r-平均凹函数,则y=f(μ(x))是A上的r次幂平均s-凹函数; (ⅳ) 若y=f(u)是I上严格递减的r次幂平均s-凹函数,u=μ(x)是A上的r-平均凸函数,则y=f(μ(x))是A上的r次幂平均s-凹函数. 证明 仅证(ⅰ),同理可证(ⅱ)、(ⅲ)、(ⅳ). 根据定义3知y=f(μ(x))是A上的r次幂平均s-凸函数. (5) 证明 设f(x)为I上的r次幂平均s-凸函数,r>0.当n=1时,t1=1,(5)式为恒等式,所以n=1时定理成立.当n=2时,∀x1,x2∈I及∀t1,t2∈[0,1]满足t1+t2=1,由r次幂平均s-凸函数的定义3有 所以当n=2时定理成立. 所以当n=k+1时,不等式(5)成立.类似可证,当r<0时(5)式仍然成立. 若f(x)为I上的r次幂平均s-凹函数,则证明中的不等号均反向,因此定理的后半部分成立.定理证毕. 定理7的一个等价形式为: 定理8 设I⊆R+,s∈(0,1],f(x)为I上的r次幂平均s-凸(凹)函数,∀xi∈I及∀pi∈R+(i=1,2,…,n),则 上式中令p1=p2=…=pn,则有: 推论 设I⊆R+,s∈(0,1],f(x)为I上的r次幂平均s-凸(凹)函数.则∀xi∈I(i=1,2,…,n),有 [1] 杨露.关于几何凸函数的不等式[J].河北大学学报(自然科学版),2002,22(2):325-328. [2] 吴善和.调和凸函数与琴生型不等式[J].四川师范大学学报(自然科学版),2004,27(4):382-386. [3] 吴善和.平方凸函数与琴生型不等式[J].首都师范大学学报(自然科学版),2005,26(1):16-21. [4] 宋振云,陈少元.调和平方凸函数及其Jensen型不等式[J].首都师范大学学报(自然科学版),2015,36(3):7-14. [5] 席博彦,包图雅.关于r-平均凸函数的一些性质[J].数学的实践与认识,2008,38(12):113-119. [6] 吴善和.GA-凸函数与琴生型不等式[J].贵州师范大学学报(自然科学版),2004,22(2):52-55. [7] 陈少元.GH-凸函数及其Jensen型不等式[J].首都师范大学学报(自然科学版),2013,34(5):1-5. [8] 宋振云,陈少元.GM-凸函数及其Jensen不等式[J].数学的实践与认识,2014,44(20):280-287. [9] 宋振云,涂琼霞.对数凸函数的几何平均型Hadamard不等式[J].湖南理工学院学报(自然科学版),2011,24(1):8-11. [10] 陈少元.AH-凸函数及其应用[J].湖北职业技术学院学报,2013,16(2):16-19. [11] 宋振云.AM-凸函数及其Jensen型不等式[J].淮北师范大学学报(自然科学版),2015,36(1):1-7. [12] GODUNOVA E K,LEVIN V I.Neravenstva dlja funkciiirokogo klassa soderžaĉego vypuklye,monotonnye I nekotorye drugie vidy funkcii[M].Moskva:MGPI,1985:138-142. [13] HUDZIK H,MALIGRANDA L.Some remarks ons-convex functions[J].Aequationes Math,1994,48:100-111. [14] DRAGOMIR S S,FITZPATRICK S.The Hadamard’s inequality fors-convex functions in the second sense[J].Dem Onstratio Math,1999,32(4):687-696. [15] KIRMACI U S.Hadamard-type inequalities fors-convex functions[J].Appl Math Comp,2007,193:26-35. [16] ALOMARI M,DARUS M.Hadamard-type inequalities fors-convex functions[J].Itn Math Forum,2008,40:1965-1975. [17] HUSSAIN S,BHATTI M I,IQBAL M.Hadamard-type inequalities fors-convex functions[J] I Punjab Univ J Math,2009,41:51-60. [18] MEHMET Z S,ERHAN S,ÖZDEMIR E M.On new inequalities of Simpson’s type fors-convex functions[J].Computers and Mathematics with Applications,2010,60:2191-2199. [19] MERVE AVCI,HAVVA KAVURMACI,ÖZDEMIR E M.New inequalities of Hermite-Hadamard type vias-convex functions in the second sense with applications[J].Applied Mathematics and Computation,2011,217:5171-5176. [20] 匡继昌,常用不等式 [M].济南:山东科学技术出版社,2010:53-63. (责任编辑:李亚军) The rth power mean s-convex function and its Jensen-type inequality SONG Zhen-yun1,CHEN Shao-yuan2,HU Fu-gao3 (1.Mechanical and Electrical Engineering School,Hubei Polytechnic Institute,Xiaogan 432000,China;2.Dean’s Office,Hubei Polytechnic Institute,Xiaogan 432000,China;3.School of Mathematics and Statistics,Hubei Engineering University,Xiaogan 432100,China) The definition ofrth power means-convex function is put forward.Several decision theorems and operation properties are given,as well as the Jensen-type inequality and its equivalent form.The results show that therth power means-convex function is extended from arithmetic convex function,geometric convex function,harmonic convex function,square convex function,harmonic square convex function andr-mean convex function,which finds a new way to study new convex functions and the extension of convex functions. s-convex function;rth power means-convex function;judgment theorem;Jensen-type inequality 1000-1832(2016)04-0019-05 10.16163/j.cnki.22-1123/n.2016.04.005 2015-09-11 教育部科学技术研究重点项目(212109). 宋振云(1958—),男,教授,主要从事高等数学教学及凸分析研究. O 178 [学科代码] 110·34 A

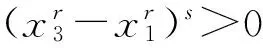




2 r次幂平均s-凸函数的Jensen型不等式