一类具有扇区和斜率约束的复杂动态网络的同步

郑海青， 郭争争， 王智剑

(石家庄铁道大学 电气与电子工程学院，河北 石家庄 050043)



一类具有扇区和斜率约束的复杂动态网络的同步

郑海青， 郭争争， 王智剑

(石家庄铁道大学 电气与电子工程学院，河北 石家庄 050043)

针对具有扇区约束和斜率约束条件的非线性Lur’e系统组成的复杂动态网络，研究其同步问题。基于Lyapunov稳定性理论，采用静态误差反馈控制方法实现被控网络的同步。利用非线性函数的凸集性质，将非线性项描述为在扇区约束和斜率约束范围内的凸组合函数，以便使等式约束条件变为不等式约束条件。求出的反馈增益矩阵可由LMI的可行解给出。最后，通过数值例子验证了所提方法的有效性。

复杂动态网络；同步；Lur’e系统；反馈控制器

0 引言

许多实际系统都可以用动态复杂网络加以描述[1-2]。同步是在复杂物理、化学和生物系统的控制中一个非常重要的过程。同步现象是复杂网络的典型动力学行为，同步在工程领域有着广泛的应用，如保密通信及谐波振荡器的产生。Lur’e系统是一类非常重要的非线性系统，其非线性满足一定的约束条件。由Lur’e系统构成的复杂动态网络的同步已经获得了很多研究人员的关注，文献[3]提出了不确定Lur’e系统的参数辨识和非线性控制器的设计技术，文献[4]提出了线性反馈控制器设计技术在混沌同步中的应用，文献[5]提出了时滞状态反馈的同步条件并分析了时滞的影响，这些同步条件均未考虑到非线性斜率限制。然而，现实中存在的一大类非线性系统同时满足扇区约束条件和斜率约束条件，以往研究者们针对具有扇区约束的非线性系统，研究其同步的成果很多，而具有斜率约束的非线性系统的同步研究结论却很少，此外，利用斜率约束条件，可以降低同步判据的保守性。

本文提出了具有扇形区域限制和斜率约束条件的非线性Lur’e型复杂网络的同步方案。所提出的同步技术基于线性静态误差控制。通过求解Lur’e型动力学系统误差绝对稳定条件，结合扇区限制和斜率限制的非线性条件以及Lyapunov稳定性条件。将等式约束条件转变为具有代表性的扇形区域和斜率限制的非线性凸函数。通过LMI技术求得反馈误差增益矩阵，最后，数值分析表明该方法的有效性。

1 预备知识

考虑如下由N个恒等节点构成的耦合复杂网络，每个节点都可用一个Lur’e系统来表示，其状态方程可描述为

式中，xi(t)表示状态变量；A∈Rn×n，B∈Rn×m；C∈Rm×n为常数矩阵；yi(t)∈Rm是系统输出；D∈Rn×n为已知的常数对称矩阵，表示网络的内部耦合矩阵；G=(gij)∈RN×N表示网络的外部耦合矩阵，其满足如下条件：如果从节点i到节点j(i≠j)之间有联系，则gij≠0，否则gij=0，对角线元素定义为

f(·)为一非线性向量值函数，记为

并且，fl(·)(l=1,2,…,m)满足以下的扇区约束条件和斜率约束条件

式中，yil(t)是系统的输出；bl和al分别是扇区约束的下限和上限；βl和αl分别是其斜率约束的下限和上限。

2 Lur’e型复杂动态网络的同步判据

同步控制的目标是找到一个控制器ui(t)使得被控网络(1)的解完全同步于s(t)。考虑网络上每个结点都加上控制器，则被控复杂网络描述如下

式中，ui∈Rn表示反馈控制输入且ui=K(xi-s)，K为静态误差反馈控制器的增益矩阵。

采用Kronecker积的形式，被控复杂网络动态系统可改写为

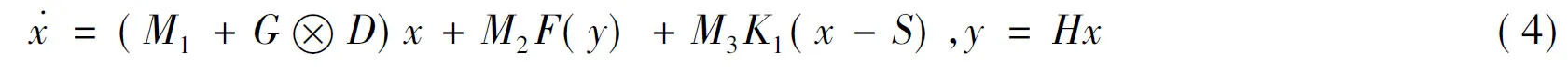
式中

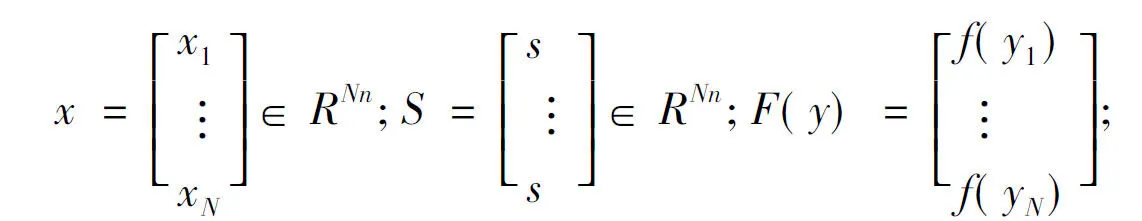
M1=IN⊗A；M2=IN⊗B；M3=IN⊗Bu；y=Hx；H=IN⊗C；K1=IN⊗K。

得到误差动态系统为

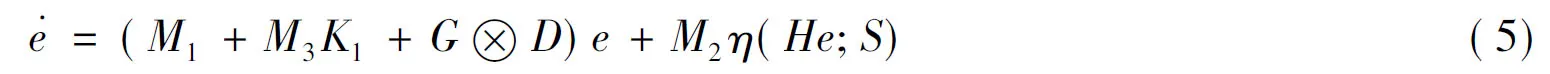
式中，η(He;S)=F(ye+ys)-F(ys),ye=(ye11,…,ye1m,…,yeNl,…,yeNm)T。

根据式(2)，可以建立关于非线性函数fl(yil)-fl(ysl)的不等式

根据误差向量的定义，得到

式中，Δl属于凸集Co{βl,αl}的元素。

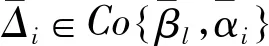
接下来，为了推导方便，做以下定义：

因此，非线性函数F(y)-F(ys)和F′(y)-F′(ys)可以写为

根据式(10)，可以得到Lur’e型复杂网络的同步判据。

命题1：若存在对称正定矩阵Q11∈Rn×n，Q22∈Rm×m和矩阵Γ∈Rm×m，X∈Rm×m，Y∈Rm×m，Z∈Rm×n，r∈Rr×n使得如下矩阵不等式成立

式中，

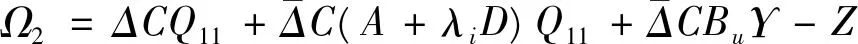
Ω3=(A+λiD)Q11+BuΥ+((A+λiD)Q11+BuΥ)T。

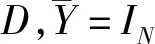
则选取的Lyapunov函数的导数为

根据式(10)，可以得到下列等式

将式(15)加到式(14)的左侧，得到

为了简单起见，定义

不等式(16)的左边分别左乘和右乘M和MT，得到

式中,

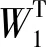
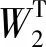
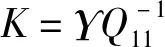
3 数值仿真

本小节通过一组相互耦合的蔡氏电路来验证上述理论分析的有效性。网络的状态方程描述为

式中，

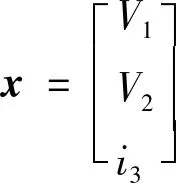
f(y)=g(V1)-Ga1V1=0.415 9V1-0.208 0[|V1+1|-|V1-1|]。

内部耦合矩阵D和外部耦合矩阵G分别取为

图1～图3是在所设计的控制器的作用下，被控网络(20)的状态响应曲线。可以看出，经过一段时间，系统的状态轨线趋于平衡点，即整个网络实现了同步。

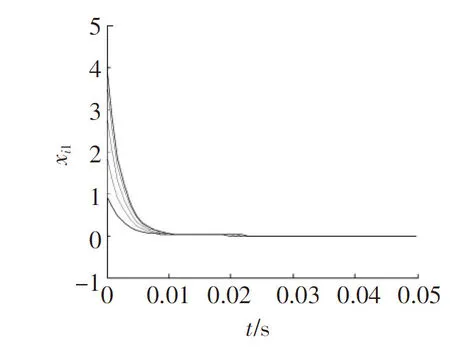
图1 状态的变化曲线

图2 状态的变化曲线

图3 状态的变化曲线

4 结论

本文研究了具有扇区约束和斜率约束的Lur’e系统构成的复杂网络的同步控制问题。与先前的同步控制方法不同，本文运用凸组合技术，将非线性性质通过等式约束条件来表示。基于Luapunov稳定性定理和非线性函数的凸约束性质，设计静态误差反馈控制器，得到使网络同步的充分条件。相应的控制增益可以通过MATLAB中的LMI工具箱得出，最后通过蔡氏电路来验证所设计的控制器的有效性。

[1]秦孝敏.基于复杂网络的城际铁路网络脆弱性分析[J].石家庄铁道大学学报：自然科学版,2014(4):82-85,89.

[2]黄树明.基于复杂网络理论的客运专线网络可靠性分析[J].石家庄铁道大学学报：自然科学版,2012(2):85-89.

[3] Wu X, Lu J. Parameter identification and back stepping control of uncertain Lu system [J]. Chaos Solitons Fractals , 2003, 18(4):721-729.

[4] Liao X X, Chen G R. On feedback-controlled synchronization of chaotic systems[J]. International Journal of Systems Science, 2003, 34 (7): 453-461.

[5] Moon Y M , Park P, Kwon W H, et al .Delay-dependent robust stabilization of uncertain state-delayed systems [ J] .International Journal of Control , 2001,74 (14):1447-1455.

Synchronization of Complex Dynamical Networks with Sector and Slope Restrict

Zheng Haiqing, Guo Zhengzheng, Wang Zhijian

(School of Electrical and Electronic Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

The problem of global synchronization is studied for a class of complex dynamical networks, where each node is a general Lur’e system with sector and slope restricted nonlinearities. A static error feedback controller based on the Lyapunov stability theory is proposed for its synchronization. The nonlinearities are expressed as convex combinations of sector and slope bounds by using convex properties of the nonlinear function so that equality constraints are converted into inequality constraints. Then, the feedback gain matrix is derived through a feasible solution of LMI. Finally, a numerical example shows the effectiveness of the proposed method.

complex dynamical network; synchronization; Lur’e system; feedback controller

2015-04-28 责任编辑:刘宪福

10.13319/j.cnki.sjztddxxbzrb.2016.02.20

郑海青(1983-),女,博士,讲师，主要研究方向为复杂网络同步与控制。E-mail:80496225@qq.com

TP13

A

2095-0373(2016)02-0102-05

郑海青，郭争争 ，王智剑.一类具有扇区和斜率约束的复杂动态网络的同步[J].石家庄铁道大学学报:自然科学版,2016,29(2):102-106.