多圆孔磁流变阻尼器准静力分析

布美娜, 邢海军, 贾 双, 杨绍普, 申永军

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)



多圆孔磁流变阻尼器准静力分析

布美娜, 邢海军, 贾 双, 杨绍普, 申永军

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

提出了一种新型多圆孔磁流变阻尼器，基于Bingham模型，推导了阻尼力计算方程。磁流变液通过多孔隙时压力梯度与磁流变液的黏度、屈服强度、孔隙阀孔径与孔数的关系为四次代数方程，应用代数方程理论得到了压力梯度的理论解。由于理论解过于复杂，采用了一种近似解计算磁流变液的压力梯度，该近似解与理论解误差很小。

磁流变阻尼器；阻尼力；Bingham模型；多圆孔

0 引言

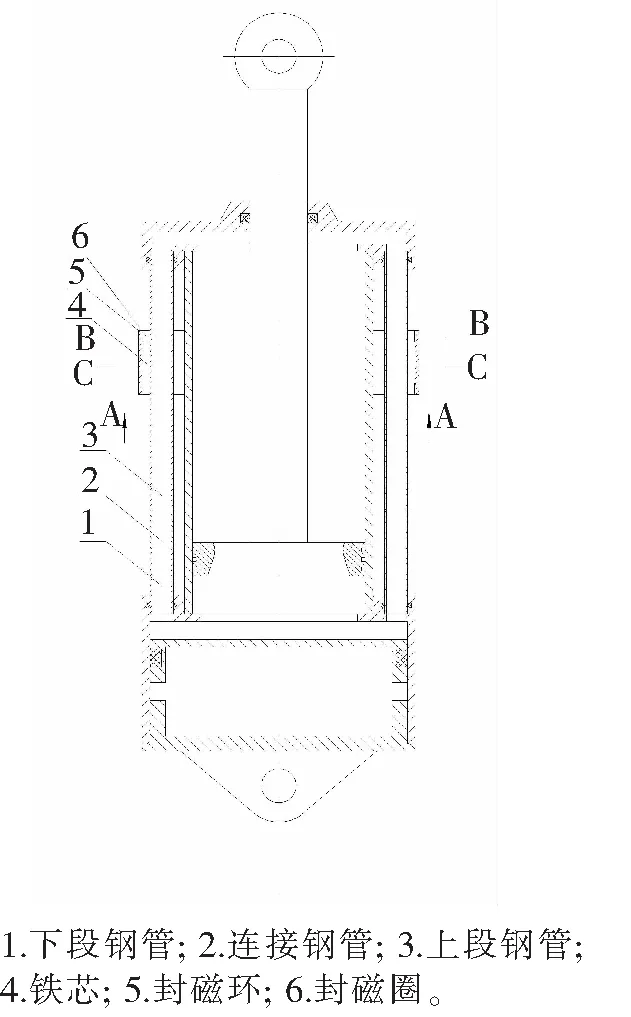
图1 MRFD结构图

磁流变阻尼器(MRFD)是一种磁流变液(MRF)应用装置，该装置利用MRF的可控特性实现阻尼力调节，配合各种控制策略，能明显降低振动指标，因而在结构抗震、车辆悬挂系统、海洋平台减振、桥梁斜拉索抗风振等各领域展现出了良好的应用前景[1-2]。国内外学者针对MRFD的阻尼力的研究主要集中在两方面，即MRFD的准静力模型与动态模型，动态模型用于动力学分析计算与半主动控制研究[3-8]，准静力学模型主要基于Bingham与Herschel-Bulkley模型研究，主要分析MRFD的结构参数、MRF的流体参数与阻尼力的关系，用于指导MRFD的设计，其中Bingham由于简单实用，应用最为广泛。MRFD的流体通道广泛采用环状阀或孔隙阀结构，杨广强[9]、Philips[10]、周云[2]等对环状阀隙结构的MRFD阻尼力进行了研究，邓志党等[11]研制了内置多孔隙阀结构的汽车用MRFD，详细推导了多孔隙阀结构MRFD阻尼力的理论计算模型并对理论分析结果进行了实验验证。文献[11]提出的阻尼力计算涉及到多个代数方程的数值求解，较为繁琐，本文基于Bingham模型，推导了MRF通过多圆孔阻尼力的计算方程，最终得到的多圆孔MRFD压力梯度与MRF的黏度、屈服强度及孔径、孔数的关系为四次代数方程，应用代数方程理论得到了压力梯度的理论解。由于理论解过于复杂，本文又采用了一种近似解计算磁流变液的压力梯度，该近似解与理论解误差很小。最后通过算例分析验证了理论分析的正确性。

1 多圆孔磁流变阻尼器

新型MRFD的结构[12]如图1所示，该阻尼器包括多个圆孔阻尼通道、磁流变液腔体 、蓄能腔体、活塞组件及电磁线圈组件(如图2所示)。

该新型磁流变阻尼器设有多个圆孔阻尼通道，每个圆孔阻尼通道包括下段钢管、连接钢管、上段钢管，分为三段钢管，能够解决样机制作时缸筒的装配问题，先将上段钢管和下段钢管分别嵌入缸盖和蓄能腔，再将连接钢管分别与上段钢管和下段钢管焊接，焊接时，上段钢管和下段钢管可转动。其中上段钢管采用不导磁材料制作。

电磁线圈组件是磁流变阻尼器产生磁场的重要结构，该结构包括铁芯、电磁线圈、两个封磁半环(如图3所示)及多个封磁盖，两个封磁半环将铁芯、电磁线圈和封磁盖包围，两个封磁半环焊接或胶结，其中铁芯采用高磁导率软磁材料制作，电磁线圈缠绕于铁芯，封磁环及封磁盖采用不导磁材料制作。当电磁线圈通电时，所产生磁力线被封闭在磁流变液缸筒、封磁环及封磁圈所包围的环形空间内，并穿过其间的上段钢管，产生垂直于上段钢管的轴线(磁流变液流动方向)的磁场，产生磁流变效应。蓄能腔内充有一定压力的氮气，用于补偿活塞组件伸缩时磁流变液腔体体积的变化。活塞及活塞密封将磁流变液腔体分割为不通的上下腔，当活塞上下往复运动时，上(下)腔的磁流变液通过多个圆孔阻尼通道回流到下(上)腔。

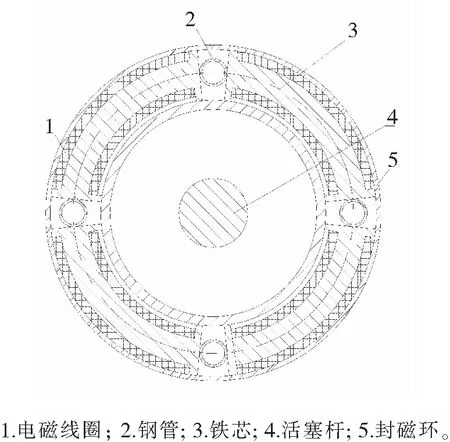
图2 C-C面剖视图

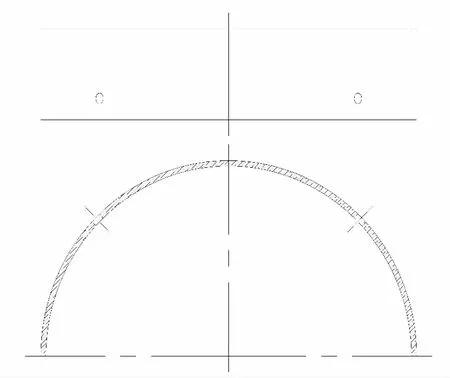
图3 封磁半环示意图

2 MRFD阻尼力方程的建立

该MRFD线圈不通电时，MRF表现为牛顿流体特性，磁流变液通流面积大，阻尼力小，同时设置多个电磁线圈组件，通电时，MRF表现为Bingham流体特性，阻尼力大，因而具有阻尼力调节范围宽的特点，本文假设圆孔对称布置，孔内的磁场强度相同，MRF流经磁场作用下的圆孔通道时，流变特性发生变化，MRFD的阻尼力受控于磁场强度。准静力分析时，引入假设：MRFD活塞以恒定速度移动；MRF稳定流动，忽略MRF惯性力。MRF Bingham模型本构关系为

MRF微元体受力分析见图4，圆孔内MRF的流速与剪应力分布见图5，忽略MRF惯性力，根据柱坐标系下Navier-Stokes方程得到MRF流经圆孔时剪应力和压力梯度的微分方程为[2]

积分式(2)为

图4 MRF微元体受力分析

图5 外置孔隙阀处MRF的流速与剪应力分布

式中，D为积分常数，该问题轴对称，r=0时，τrx(r)=0，因此D=0，所以

当τrx≥-τ0时，液体之间无相对运动，形成塞流区，τrx(r)<-τ0液体之间有相对流动，存在剪切率，液体之间存在相对速度，根据图5，由(4)式得塞流区半径为

积分式(6)得

式(7)的边界条件为r=r2时，ux(r)=-v0，塞流区MRF流速为

MRF流经n个相同直径的圆孔时，体积流速为

式中，Ap为活塞的有效面积，将式(7)、式(8)代入式(9)，应用分部积分法积分得

3 MRFD阻尼力方程求解

将式(5)代入式(10)，并令

整理后得到无量刚阻尼力方程为

式中，P为无量纲压力梯度；T为无量纲屈服强度。

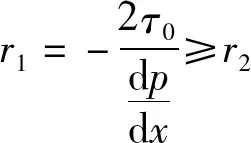
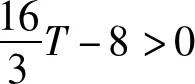
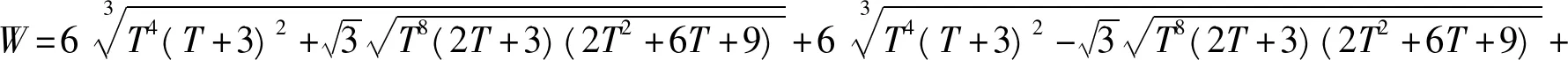
P=-2T-PP为方程(13)的解，P为负值，按习惯将阻尼力写为正值，最终无量纲压力梯度解为

当τ0=MRF为牛顿黏性流体，此时无量纲屈服强度T=0，无量纲压力梯度的解P=8。式(16)非常复杂，进一步的研究结果表明P可以用下式简化计算

图6为式(17)计算结果，图7为式(17)计算结果与理论解(16)的相对误差，当T=196.513时，相对误差最大，仅为2.51%，说明式(17)计算结果很接近理论解。

设磁场作用于圆孔的有效区域长度为l，该区域内磁场均匀，根据式(11)得到MRFD的阻尼力为

图6 简化计算式(17)计算结果

图7 简化解与理论解相对误差

4 算例分析

根据图1结构，取MRF的黏度η=1.5 Pa·s，圆孔有效区域长度l=20 mm，计算结果见图8～图11。图8为圆孔数为5时阻尼力计算值，表明τ0取不同值时，MRFD的阻尼特性变化很大，随τ0的增加，阻尼力会明显增加。图9为不同孔数时阻尼力计算值，阻尼力随孔数的增加而减小，当活塞速度较大时，这种现象会更明显。图10为不同孔径下的阻尼力计算值，阻尼力随孔径的增加而减小。图11为不同活塞面积阻尼力计算值，阻尼力随活塞有效面积的增加而增加。图8～图11的计算结果反映了MRF性能参数与MRFD结构参数对MRFD阻尼力的影响，与直观的物理特性判断一致，证明了前述理论分析的正确。

AP=2 000 mm2 n=5 r2=4 mm

AP=2 000 mm2 τ0=50 kPa r2=4 mm

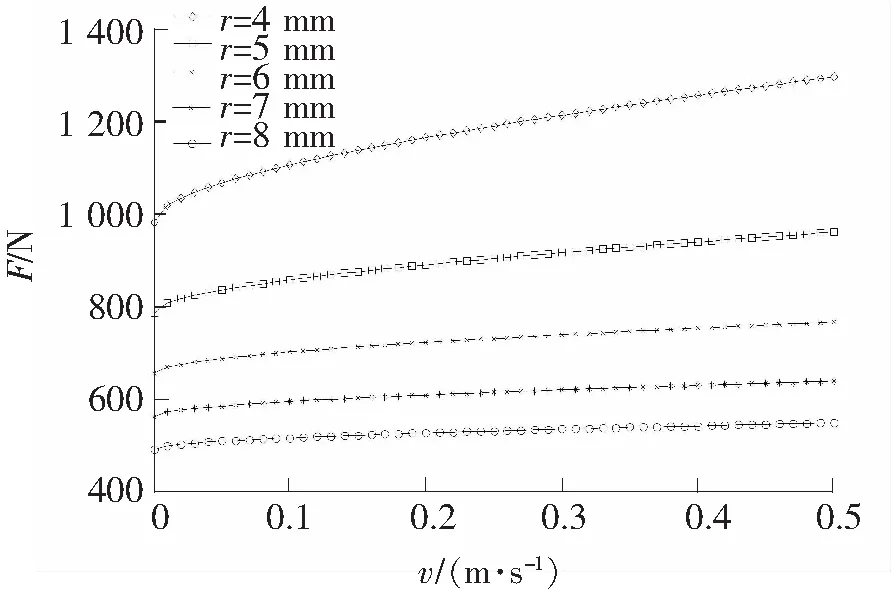
AP=2 000 mm2 n=5 τ0=50 kPa

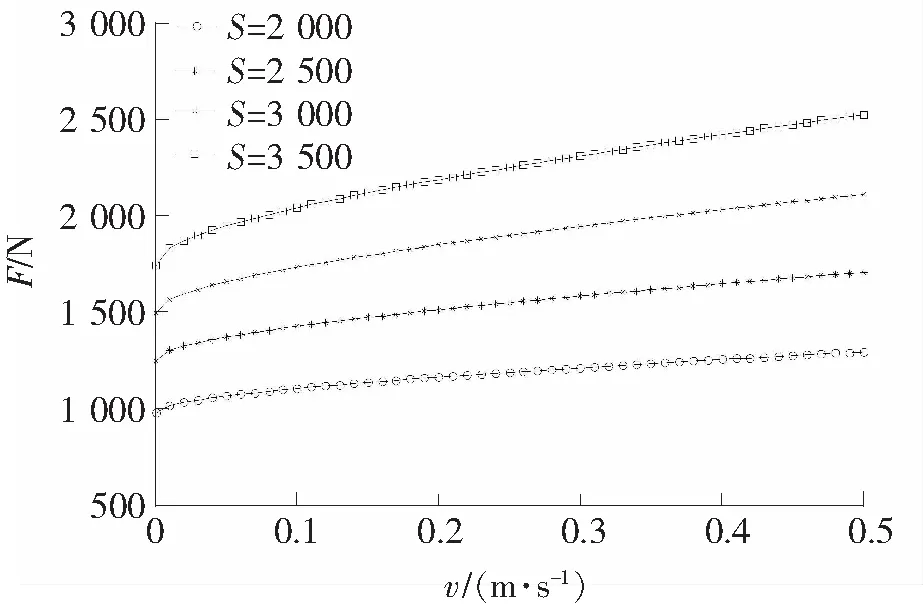
n=5 τ0=50 kPa r2=4 mm

5 结 语

基于Bingham模型，推导了多圆孔MRFD的压力梯度求解方程，求得了MRFD压力梯度的理论解。由于理论解的表达式复杂，不便应用，在分析理论解的基础上，得到了近似解，该近似解与理论解非常接近，表达式简单，便于应用。最后的算例分析结果证明了理论分析的正确。

[1]杜林平, 孙树林．磁流变阻尼器在结构振动控制中的应用[J]．噪声与振动控制，2011(2):127-130.

[2]周云，谭平．磁流变阻尼控制理论与技术[M]．北京：科学出版社，2007.

[3]邓志党，高峰，刘献栋，等．磁流变阻尼器力学模型的研究现状[J]．振动与冲击，2006，25(3)：120-126.

[4]陈忠海,杨全,宁响亮,等. 磁流变阻尼器的设计、试验及其减振性能研究[J]. 地震工程与工程振动,2014(1):204-210.

[5]Yang Shaopu, Li Shaohua, Wang Xiaojie, et al.A hysteresis model for magneto-rheological damper[J].International Journal of Nonlinear Sciences and Numerical Simulation,2005,6(2):139-144.

[6]Balamurugan L,Jancirani J,Eltantawie M A. Generalized magnetorheological (MR) damper model and its application in semi-active control of vehicle suspension system[J]. International Journal of Automotive Technology,2014,153:7.

[7]Wu Fusen, Huang Yijian, Huang Kai, Xu Shan. Trispectrum and correlation dimension analysis of magnetorheological damper in vibration screen[J]. Journal of Central South University,2012,19(7):1832-1838.

[8]Shuqi G, Shaopu Y, Cunzhi P. Dynamic modeling of magnetorheological damper behaviors[J]. Journal of Intelligent material systems and structures,2006,17(1):3-14.

[9]Yang G, Large-scale magnetorheological fluid damper for vibration mitigation: modeling, testing and control, PHD dissertation[D].Indiana: University of Nortre Dame, 2001.

[10]Philips R W.Engineering applications of fluids with variable yield stress[D] .California:Ph.D Dissertation University,1976.

[11]邓志党，高峰，刘献栋,等．汽车磁流变减振器阻尼特性理论计算与试验[J]．机械工程学报，2008，44(8)：202-207.

[12]邢海军，布美娜，杨绍普,等．外置多圆孔阻尼通道磁流变阻尼器：中国，CN201410666465[P].2014-11-20.

Quasi-static Analysis of Magnetorheological Dampers with Multi-hole-ducts Valve

Bu Meina, Xing Haijun, Jia Shuang, Yang Shaopu, Shen Yongjun

(School of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

In this paper，the damping force of Magnetorheological dampers with multi-hole-ducts valve is analyzed using quasi-static axi-symmetric model. Based on Bingham model，the equation of Magnetorheological fluid through outlay multi-hole-ducts valve is derived. The relationship between the pressure gradient，the structure parameters of MR damper and the performance parameters of Magnetorheological fluid is shown as a quartic algebraic equation. The analytical solution of the pressure gradient equation is obtained by algebraic equation theory. Because of the complexity of the analytical solution，an approximate solution which is in close agreement with the analytical solution is given.

magnetorheological damper; damping force; Bingham model; multi-hole-ducts valve

2015-05-07 责任编辑:车轩玉

10.13319/j.cnki.sjztddxxbzrb.2016.02.15

河北省科技支撑项目(14212202D)；河北省高校重点学科建设项目；河北省高等学校创新团队领军人才培育计划项目(LJRC018)

布美娜(1990-)，女，硕士研究生,主要从事机械设计及理论的研究。E-mail: 18830119658@163.com

TH122 ；O241

A

2095-0373(2016)02-0078-06

布美娜,邢海军,贾双,等.多圆孔磁流变阻尼器准静力分析[J].石家庄铁道大学学报:自然科学版,2016,29(2):78-82.