带拒绝费用的平行机在线排序

荣建华 侯丽英

(1.石家庄铁道大学 四方学院 基础部，河北 石家庄 051132，2.南京农业大学 理学院，江苏 南京 210095)



带拒绝费用的平行机在线排序

荣建华1侯丽英2

(1.石家庄铁道大学 四方学院 基础部，河北 石家庄 051132，2.南京农业大学 理学院，江苏 南京 210095)

研究了工件带有拒绝费用的m台平行机在线算法，假定有m台平行机M1,M2,…,Mm，n个工件J1,J2,…,Jn,每个工件的加工时间与拒绝费用成固定的比例α(α≥0)，即pj=αtj，当α较大时，即工件的拒绝费用相对于加工时间较大，则将此工件接收加工；当α较小时，即每个工件的拒绝费用相对于其加工时间较小，此时将工件拒绝。文中设计出在线算法PRLS,并证明算法的竞争比为关于参数α的分段函数，且为紧界。

在线排序； 竞争比； 同型机； 拒绝费用；不可中断;运筹学

0 引言

在经典的排序文献中，所有的工件都不允许被拒绝，换言之，任何工件都必须被安排到机器上进行加工。然而在工厂实际生产过程中，生产决策者们并非总是如此。随着社会经济的迅速发展，市场竞争也越来越激烈，为了使企业在市场竞争中立于不败之地，良好的调度管理和有效的控制成本成为企业间竞争的重要因素。因此在现有的生产资源有限的前提下，为了使企业获得最多的利润，生产厂家有时不得不拒绝一些资源耗费较多但带来的利润却较少的工件。基于在实际生产中上述问题比较常见，所以工件带拒绝费用的排序问题受到研究人员广泛的关注[1-4]。本文主要研究了工件带拒绝费用的m台平行机在线排序问题。基本模型描述如下：设有m台机器M1,M2,…,Mm和n个工件J1,J2,…,Jn，每台机器的加工速度相同，每个工件Jj带两个参数(pj,tj),pj表示其拒绝费用，tj表示其加工时间。当工件Jj到达后，生产决策者需马上做出决定，工件可以被拒绝，但要付出一定的拒绝费用；也可以选择被加工，花费一定的加工时间。目标为拒绝工件的总拒绝费用与加工工件的最晚完工时间(makespan)之和最小。文中进一步假设每个工件的拒绝费用和加工时间成固定比例α(α≥0)，且加工不允许中断(non-preemptive)，即工件一旦分给某个机器，必须由这台机器连续加工直到结束。以上问题用三参数法表示为Pm|nonpmpt,rej,pj=αtj|W。

根据确定排序时了解的工件信息的多少，常将平行机排序分为“在线”(on-line)，“离线”(off-line)和“半在线”(semi on-line)。在线排序为工件一个一个到达，只有在工件到达后才知道它的信息，且工件一经安排不得临时改变；离线排序为所有工件信息都事先完全已知，排序者可充分利用工件信息设计算法；而实际应用中的情况往往介于上述两种情形之间，我们称之为“半在线”(semion-line),即所知道的工件信息介于在线和离线之间，工件的准确信息虽然未知，但一些局部信息事先已知，如：工件按从小到大的顺序到达,各工件的加工时间介于某个区间[t,rt]中，工件的总长度(sum),最大工件(max)等等。半在线排序中，已知的工件部分信息或条件可以帮助我们设计出比在线情形更优的算法。

对于排序问题，人们致力于研究它的近似算法，通常用竞争比ρA来衡量算法A的优劣。设CA(I)为用算法A安排实例I所得的目标值，COPT(I)为离线排序下的最优值，则定义ρA=inf{l|CA(I)≤lCOPT(I),∀I}一个排序问题具有下界ρL是指不存在一个算法A，其竞争比严格小于ρL。如果某算法A的竞争比与其相应的下界相等，即ρA=ρL，则称该算法为最佳近似算法。

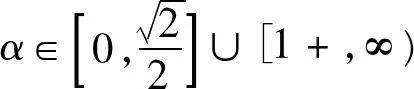
本文是基于闵啸[6-7]的基础上，将机器台数推广到任意台m(m>3)，即讨论m台带拒绝费用的同型机在线排序问题，每个工件的拒绝费用pj和加工时间tj之间成固定比例α，即pj=αtj(α≥0)，且加工不允许中断(non-preemptive),问题记为Pm|nonpmpt,rej,pj=αtj|W，设计出在线算法PRLS，证明算法的竞争比ρPRLS为关于参数α和机器台数m的分段函数。

1 Pm|nonpmpt,rej,pj=αtj|W的算法设计

Pm|nonpmpt,rej,pj=αtj|W问题的描述已在引言中介绍，其中，α为工件的加工时间和拒绝费用的比例(α≥0)，下面对符号作统一规定。

算法的基本思想：若α较大，即工件的拒绝费用相对于加工时间较大，则倾向于将其接收，若α较小，即每个工件的拒绝费用相对于其加工时间较小，故将其拒绝较好；因为同型机在线排序中，对于加工不可中断情形，且m台机器时，LS(listscheduling)算法已为最优算法，故可按LS算法安排工件加工。

算法PRLS:

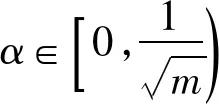
引理1.1在m台同型机在线排序中，假设S为被加工的工件集，且按LS算法安排加工，y为最后完工的工件，最晚完工时间为C(S)，则有：

(2)L(S)≤mC(S)。

定理1.1PRLS算法的竞争比至多为：

且界是紧的。

证明：根据α的不同取值范围，下面分情况进行讨论。

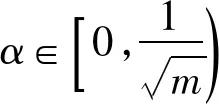
以下根据x在最优解中是被接收还是被拒绝再分两种子情形：

子情形2.2：若x在最优解中被接收，则有：x∈A，

由此，得到了关于算法PRLS的上界ρPRLS。

下面构造实例说明这个界是紧的。

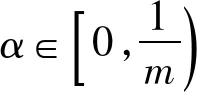
2 结语

本文将带拒绝费用的平行机排序问题推广到m台机器上，且不允许中断加工，设计出在线算法PRLS，并证明了算法的竞争比为关于参数α的分段函数。但是有关该问题的下界还没有给出，下一步将致力于构造该问题的下界。

[1]SEIDEN S S. Preemptive multiprocessor scheduling with rejection[J].Theoretical Computer Science,2001,262:437-458.

[2]WEN J J,DU D L. Preemptive on-line scheduling for uniform processors[J].Operations Research Letters,1998,23:113-116.

[3]Epstein L,Sgall J. Approximation schemes for scheduling on uniformly related and identical parallel machines[J]. Algorithmica,2004,39:43-57.

[4]Dosa G,He Y. Preemption and non-preemption on-line algorithms for schuduling with rejection on two uniform machines[J].Computing,2006,76：149-162.

[5]Bartal Y,Leonardi S,Marchetti-Spaccamela A,et al. Multiprocessor scheduling with rejection[J].SIAM J on Discrete Mathematics, 2000,13:64-78.

[6]闵啸. 一种特殊情形不可中断的两台可拒绝同型机在线排序问题[J].数学的实践与认识，2006,36(4)：1-6.

[7]闵啸. 一特殊情形的三台可拒绝同型机在线排序问题[J].嘉兴学院学报，2006,18(3)：44-47.

On-line Scheduling on Identical Machines with Rejection

Rong Jianhua1, Hou Liying2

(1.Department of basic,Shi jiazhuang Tiedao University Sifang College,Shijiazhuang 051132,China;2.College of Sciences,Nanjing Agricultural University,Nanjing 210095,China)

This paper investigates the on-line scheduling problem on m identical machines with rejection . An identical processors system denoted by and a sequence of independent jobs are given.We assume that the processing time of each job and its penalty forms the regular proportion denoted by.The objective is to minimize the sum of the makespan produced by the accepted jobs and the total penalty of the jobs which have been rejected.Preemption is not allowed.For this version,we present an on-line algorithm and prove the competitive ratio.

on-line scheduling; competitive ratio; identical machine; rejection; nonpreemptive; operations research

2015-04-06 责任编辑:车轩玉

10.13319/j.cnki.sjztddxxbzrb.2016.02.21

国家自然科学基金(11426133), 南京农业大学青年科技创新基金(0506J0116)

荣建华(1981-)，女，硕士，讲师，主要从事运筹学与组合最优化研究。E-mail:rongjianhua2006@126.com

O223

A

2095-0373(2016)02-0107-04

荣建华，侯丽英.带拒绝费用的平行机在线排序[J].石家庄铁道大学学报:自然科学版,2016,29(2):107-110.