病态矩阵参数估计的改进主元加权迭代算法

潘 轶，岳建平，刘 斌

（1.河海大学 地球科学与工程学院，江苏 南京 210098）

病态矩阵参数估计的改进主元加权迭代算法

潘 轶1，岳建平1，刘 斌1

（1.河海大学 地球科学与工程学院，江苏 南京 210098）

传统测绘数据处理中矩阵求逆的准确性极大地影响最终解算精度。针对测量数据处理常遇到的病态矩阵求逆不稳定，导致精度显著降低等问题，提出一种改进的主元加权迭代法的病态矩阵处理算法。该算法结合传统主元加权迭代法精度高、误差转移法稳定性好的优点，先将误差从解向量转至中间变量，再利用主元加权迭代法求解中间变量，实现更高精度的解算结果。实验表明，改进算法在良态矩阵法方程中解算结果与传统方法一致，在病态矩阵中改进算法精度更高。

参数估计；病态矩阵；改进主元加权迭代；误差转移

一直以来，病态问题存在于测绘领域的方方面面，比如控制网平差、坐标转换、GPS快速定位计算、形变分析、大地测量反演、卫星重力向下延拓、航天飞行器的精密轨道解等[1]。在这些测量数据的处理中，病态矩阵求逆的不稳定性导致最终解算精度显著降低，该问题亟待解决。针对测绘领域中的病态问题，国内外学者做过一系列研究，并取得相应成果。王乐洋等[2]采用岭估计法处理加权总体最小二乘平差的病态性问题；郭海涛等[3]提出利用广义岭估计解决单线阵CCD卫星影像外方位元素解算中法方程病态问题，该方法简便、稳定；Gui Q M等[4]提出基于奇异值分解的有偏估计，并将其应用于大地测量病态问题中；Wang Z[5]先基于Tikhonov正则化法选择合适的正则化矩阵R 削弱法方程病态，再结合 Lambda方法确定整周模糊度，得到一种解决单频接收机快速定位系统中病态问题的新算法。Vajargah等[6]利用遗传算法找到2个可逆对角阵，并将其条件数缩放至最小，降低病态程度。王永弟等[7]先使用主元加权进行预处理，再构造迭代公式迭代处理病态问题，大大提高解的精度。胡圣荣等[8]提出了误差转移法，将误差从解向量转移到中间变量，提高解的精度与稳定性。

本文将误差转移法与主元加权迭代法相结合，研究了一种新算法。在矩阵分别为良态和病态情况下，将其应用效果与其他算法如高斯约化法、传统主元加权迭代法进行对比分析，得出结论。

1 改进主元加权迭代法原理

1.1 传统主元加权迭代法

一般情况下，参数估计线性化后的方程组的形式如下：

式中，A为系数矩阵；b为常数项；x为所求解向量。若令α为权因子，E为n阶单位矩阵，则传统主元加权法将式（1）左右两端各加上ax，得：

通常根据条件数的大小衡量线性方程组的病态程度：系数矩阵A的条件数越大，方程组病态程度越大。根据文献[9]可得，对于正定对称矩阵A，当α＞0时，则cond（A+αE）＜cond（A）。其中cond表示条件数。将式（1）变换为式（2），减小了条件数，从而减轻了线性方程组的病态程度。

因式（2）两端都含有解x，可构造迭代公式：

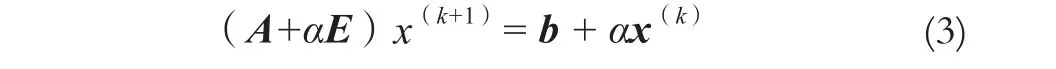
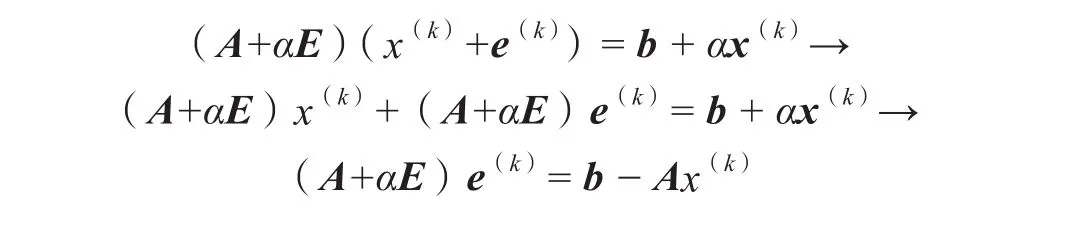
1.2 改进主元加权迭代法

传统主元加权迭代法精度已经很高，为了进一步提高解算结果的精度与稳定性，本文在传统主元加权迭代法的基础上引入误差转移法，得到一种新的病态矩阵处理算法——改进主元加权迭代法。显然，对病态方程组 Ax = b直接求解时，解x误差太大。本文算法先引入C，变换式（1），得到：

其中，C为n×n非奇异矩阵。根据式（4），求解出的解向量y误差虽大，但通过式（5）能够得到误差很小的解x：

简而言之，这一步骤将误差体现在中间变量y上而避开解x，即将解x的误差转移到y上，提高了解x的精度。文献[6]中取C = AT实际效果较好。再在变换后的方程组式（4）左右两端各加上αx，得：

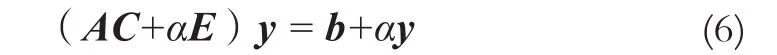
再根据迭代公式

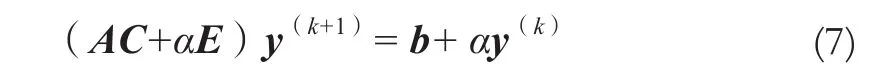
求解，得到中间变量y。最后通过式（5）得到更精确的解x。

本文结合误差转移与主元加权迭代法，得到一种改进的主元加权迭代法。即先将x替换为Cy，利用主元加权迭代法求解ACy = b，得到中间向量y；再由x=Cy得到解x。该方法在主元加权迭代法的基础上，加入误差转移，进一步提高了解的精度与稳定性。该方法在Mmatlab中的解算步骤如下：

1）选取C，变换Ax=b为ACy=b；

2）选取α，选取初始点y（0），利用三角分解法求解（AC+αE）y（1）= b+ αy（0），得到y（1）；

3）进入循环，计算r（k）= b - AC y（k）；

4）求解（AC+αE）e（k）= r（k）；

5）计算y（k+1）= y（k）+e（k）；

7）计算x=Cy，得到解向量x。该方法的流程图如图1所示。

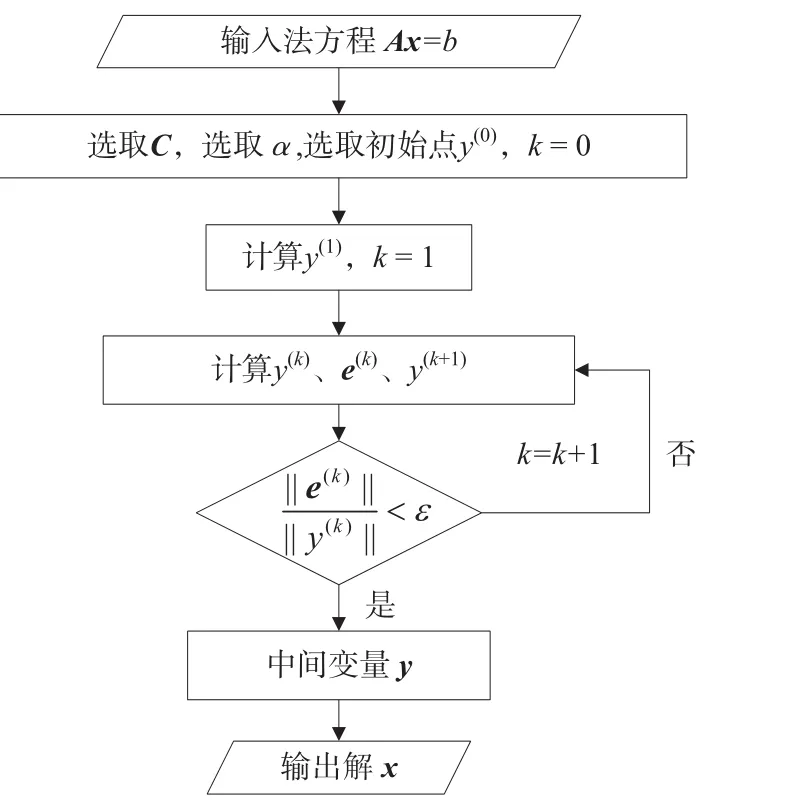
图1 改进主元加权迭代法

2 算例分析

下面就各方程组分别为良态和病态2种情况下，利用高斯约化法、主元加权迭代法、改进主元加权迭代法3种方法进行求解，并对解的结果进行对比分析。

2.1 良态线性方程组求解

某三角网坐标平差的法方程如式（8）所示[10]：

式（8）的系数矩阵A的条件数为2.714 7，该线性方程组为良态方程组。利用高斯约化法、主元加权迭代法、改进主元加权迭代法3种方法分别对其进行求解，计算结果如表1所示。

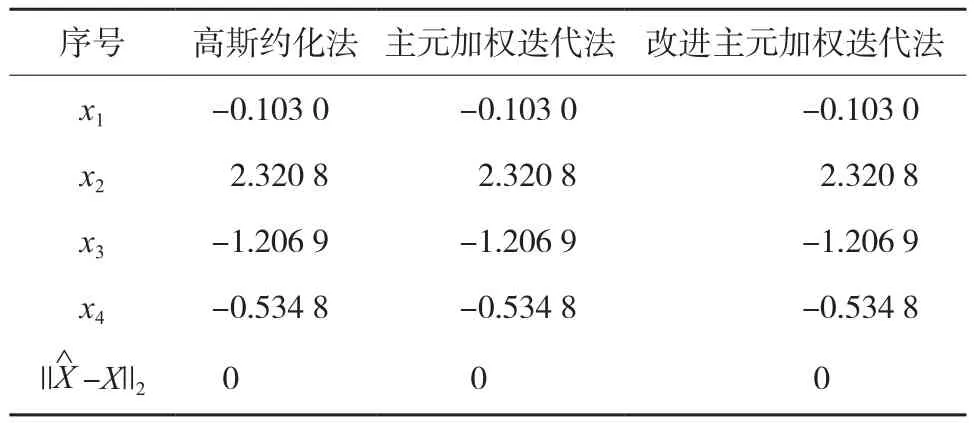
表1 计算结果

由表1中的计算结果可知，当线性方程组为良态时，无论是主元加权迭代法，还是本文中的改进主元加权迭代法，计算结果都与高斯约化法相同。

2.2 病态线性方程组求解

为了证明本文方法的通用性，选取文献[11]中一个例子：

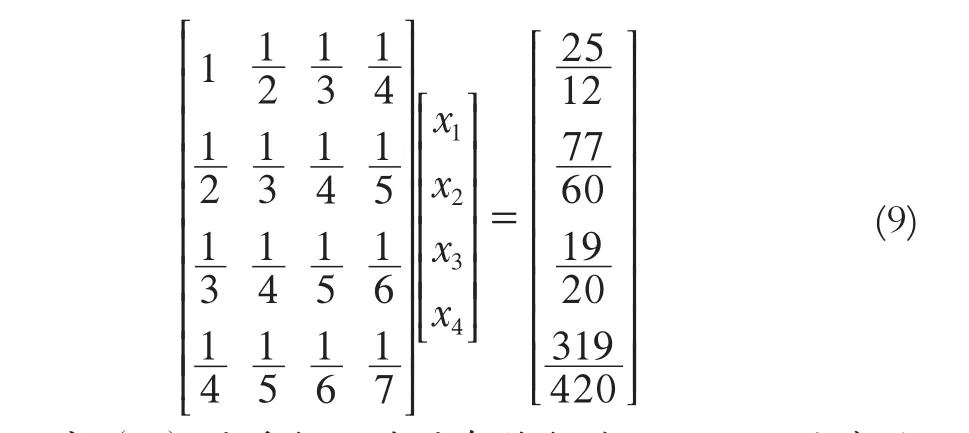
其中，式（9）的系数矩阵的条件数为15 514，该线性方程组为病态方程组。本例的精确解为[x1x2x3x4]T= [1 1 1 1]T。对常数项进行扰动，取为[2.083 3 1.283 3 0.950 0 0.797 5]T。利用高斯约化法、主元加权迭代法、改进主元加权迭代法3种方法对方程组（9）进行求解，计算结果如表2所示。

由表2中的计算结果可知，当线性方程组为病态时，高斯约化法、主元加权迭代法、改进加权迭代法3种方法参数真值与估值之差的范数分别为 202.000 0、0.186 7和0.117 5。相对于高斯约化法，利用主元加权迭代法与改进加权迭代法得到的计算结果精度大大提高；相对于主元加权迭代法，使用本文中的改进主元加权迭代法获得的计算结果精度更高。

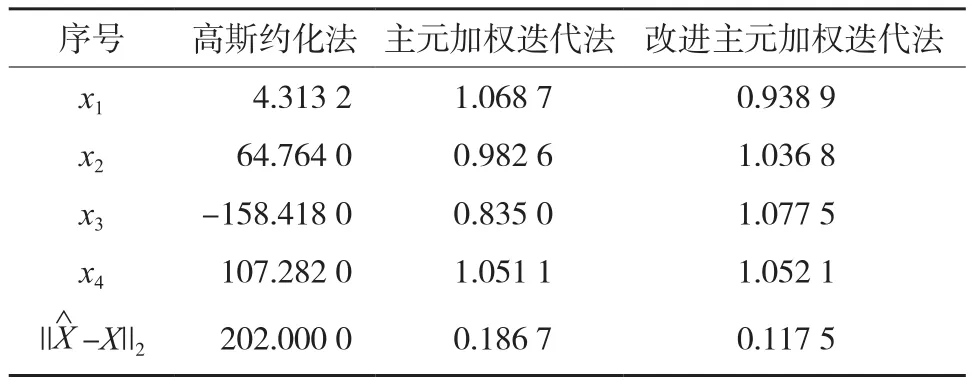
表2 计算结果1

为了进一步证明本文方法在测量数据处理中的作用，再选取文献[12]中一个例子。该算例的设计阵与观测值如表3所示。

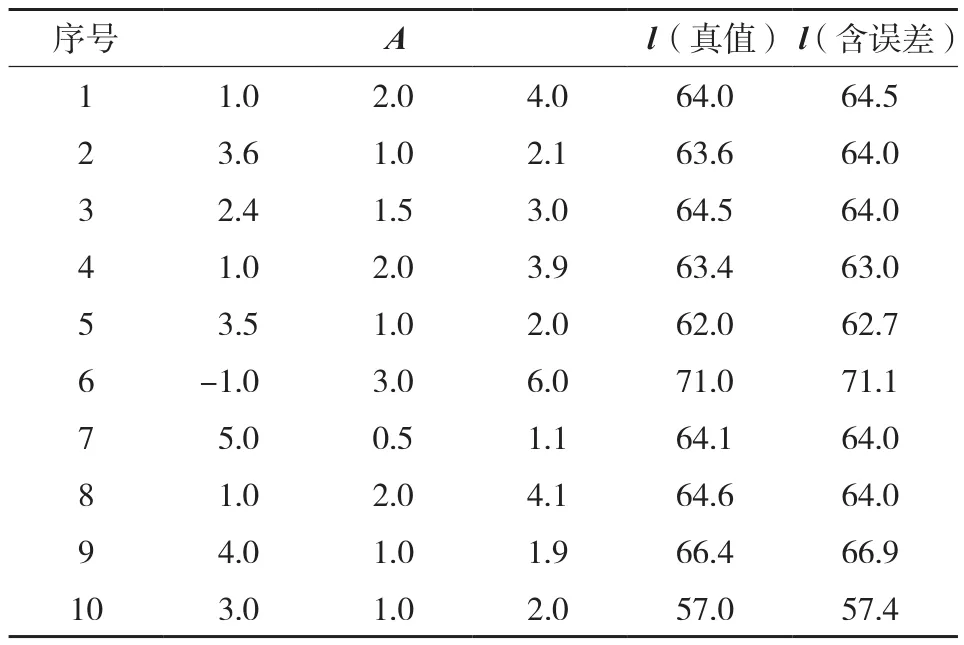
表3 设计阵与观测值

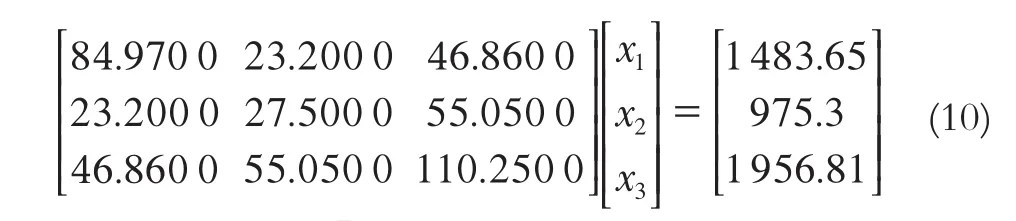
其中，法矩阵ATA的条件数为1.794×104，易得ATAx=ATl为严重病态线性方程组。该病态线性方程组有3个未知数，其精确解为

利用高斯约化法、主元加权迭代法、改进主元加权迭代法3种方法对病态线性方程组ATAx=ATl进行求解，计算结果如表4所示。

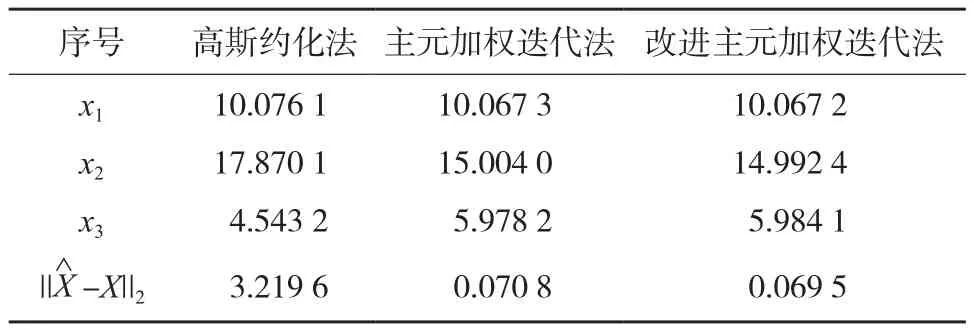
表4 计算结果2

由表4中的计算结果可知，当线性方程组为病态时，高斯约化法、主元加权迭代法、改进加权迭代法3种方法参数真值与估值之差的范数分别为3.219 6，0.070 8和0.069 5。相对于高斯约化法，利用主元加权迭代法与改进加权迭代法得到的计算结果精度得到较大提高；相对于主元加权迭代法，使用本文中的改进主元加权迭代法获得的计算结果精度更高。

通过以上3个算例可得，无论是在线性方程组为良态还是病态时，利用改进主元加权迭代法求解的结果都非常接近真值。相对于传统算法，本文中的主元加权迭代法的求解精度有一定的提高。

3 结 语

病态模型的求解一直是测绘领域中常常遇到的问题。相对于传统算法，本文提出一种改进主元加权迭代法，并分别在方程组为良态和病态时，将其应用效果与高斯约化法、主元加权迭代法进行对比分析。计算结果表明，本文算法适用性强、求解精度高。但本文只将该算法与个别算法进行比较，与其他算法的对比还有待研究。

[1] 王振杰,欧吉坤.大地测量中不适定问题的正则化解法研究[D].北京：中国科学院研究生院,2003

[2] 王乐洋,许才军,鲁铁定.病态加权总体最小二乘平差的岭估计解法[J].武汉大学学报(信息科学版),2010,35(11)：1 346-1 350

[3] 郭海涛,张保明,归庆明.广义岭估计在解算单线阵CCD卫星影像外方位元素中的应用[J].武汉大学学报(信息科学版),2003,28(4)：444-447

[4] GUI Q M, GUo J F, oU J K. Biased Estimation Based on SVD and Its Application in Geodetic Adjustment[J].Bollettino di Geodesia e Science Aiffni,2002(61)：99-106

[5] WANG Z. A New Approach to Ill-conditioned Problems in Rapid Positioning Using Single Frequency GPS Receivers (IoN GPS/GNSS 2003) [A]//Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation [C]. Portland, oR： oregon Convention Center, 2003. 1 229-1 239

[6] VAJARGAH B F, MoRADI M. Diagonal Scaling of Ill-Conditioned Matrixes by Genetic Algorithm[J]. Journal of Applied Mathematics, Statistics and Informatics,2012, 8(1)：49-53

[7] 王永弟,赵好好.病态线性模型参数估计的主元加权迭代法[J].测绘通报,2014(2)：23-25

[8] 胡圣荣,罗锡文.病态线性方程组的新解法：误差转移法[J].华南农业大学学报,2001,22(4)：92-94

[9] 唐丽,李鹏飞.主元加权迭代法求解病态线性方程组[J].科学技术与工程,2012,12 (2)：381-383

[10] 武汉测绘科技大学测量平差教研室.测量平差基础[M].北京：测绘出版社,1996

[11] HoFMANN B, MAT P. SomeNote on the Modulus of Continuity for Ill-posed Problems in Hilbert Space [J]. Weierstraß Institute for Applied Analysis and Stochastics, 2011, 16(6)：34-41

[12] 周江文,黄幼才.抗差最小二乘法[M].武汉：华中理工大学出版社,1997

P207

B

1672-4623（2016）08-0064-03

10.3969/j.issn.1672-4623.2016.08.021

潘轶，硕士研究生，研究方向为精密工程测量。

2015-11-09。

项目来源：国家自然科学基金资助项目（41174002）。