基于应变波形的船舶推进轴系负荷测量方法研究

汪 骥， 樊 荣, 李 瑞, 刘玉君, 王诗源

( 1.工业装备结构分析国家重点实验室， 辽宁 大连 116024；2.高新船舶与深海开发装备协同创新中心， 上海 200240；3.Bluecross blueshield of tennessee， Chattanooga Tennessee 37402, USA)



基于应变波形的船舶推进轴系负荷测量方法研究

汪 骥1,2， 樊 荣1, 李 瑞1, 刘玉君1, 王诗源3

( 1.工业装备结构分析国家重点实验室， 辽宁 大连 116024；2.高新船舶与深海开发装备协同创新中心， 上海 200240；3.Bluecross blueshield of tennessee， Chattanooga Tennessee 37402, USA)

应变片法是船舶推进轴系负荷测量的常用方法。传统的应变片法由于测量时需要停车记录数据，测量过程较为繁琐，且测量点数有限，误差较大。改进应变片测量方法，首先利用应变仪采集完整的应变波形，无需中途停车。然后通过分析轴低速转动时的应变波形，滤除相关误差点，推导出轴系截面最大应变值，得到轴截面弯矩，最终结合力和弯矩的平衡方程，求出各轴承负荷分配情况。经过实船数据采集计算，证明了该测量方法的可行性。

应变片法 轴系校中 应变波形 轴承负荷

0 引言

船舶推进轴系是船舶推进系统的重要组成部分，是船舶的关键部件之一[1]。船舶轴系校中的优劣，直接关系到船舶能否保持长期正常运转以及航行安全。船舶轴系负荷测量是评价船舶轴系校中优劣的措施之一，同时也是轴系校中的重要依据[2]。

目前，常用的轴系负荷测量方法主要有顶举法和应变片法。顶举法测量设备简单，但对于船体密封部分却无法实施。应变片法相对于顶举法测量精度高，且可测量因船体密封而无法采用顶举法测量的轴承负荷。部分船厂和船级社采用应变片法来测量轴系负荷。

现有的应变片法是在应变片布置完毕后，使用盘车机转动到固定点(正向盘车：90°，180°，270°，360°；反向盘车：270°，180°，90°,0°)记录应变仪上相应的应变值。这种方法要多次停车，操作较为繁琐，且收集应变会存在相当大的误差。这是因为，首先，工程实际中很难将传动轴准确地停到预设位置，这种情况下记录的应变值存在误差。再者，在传动轴停止时记录数据，应变片应变不是很稳定，还会出现跳动，也会产生误差。

针对以上问题，采用分析应变波形的方法，对传统应变片测量方法进行改进。在盘车机的带动下转动轴系，同时应变仪采集完整的应变波形数据，中途无需停车。由于盘车机转速较低，可忽略转速对轴系及负荷的影响。不仅能够解决停车时位置判断的问题，而且根据轴系低速转动时的应变波形特征，可以对应变片某些异常点进行修正，采用多组弯曲应变数据算得轴截面最大应变，进而求得轴截面弯矩，避免因一组数据偶然误差而造成弯矩结果误差偏大。结合力和弯矩的平衡方程，求出各轴承负荷分配情况。

1 轴系转动时弯曲应变分析

1.1 轴系转动时弯曲应变变化规律

轴系静止时，由于轴自重作用，轴系产生弯曲变形。轴截面处弯曲应变分布如图1所示，弯曲应变在截面处，距中性轴远近成线性分布。其表达式为

式中：z为测点到中性轴的距离；ρ为弯曲中性线的弯曲半径。

图1 轴截面弯曲应力分布图

而圆截面的中性轴通过截面形心，所以在截面上下两点处(距中性轴R)应变最大，设最大应变为a，带入式(1)中，则轴截面处弯曲应变为

式中：R为截面半径。

当轴系转动时，应变片随之转动，相应的测点位置发生变化，如图2所示。设轴转动了β角度，则应变片测点距中性轴距离z变为Rcosβ，且如果轴系的受力不变，截面弯矩M为定值，则端面最大弯曲应变仍然为a，带入式(2)中，则应变片处的应变为ε=acosβ。如果轴系为恒速转动，设速度为ω，则此时应变片处应变随时间变化形式为一简谐量[3]：

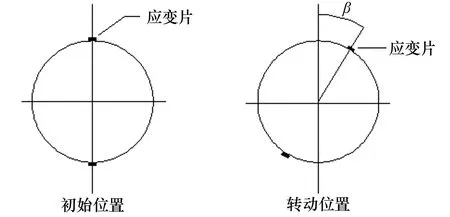
图2 应变片转动位置示意图

此应变信号的频率和轴系转动的频率相同。如果轴系转动中存在某种激振力，则截面弯矩中也存在简谐成份，相应的最大弯曲应变也存在简谐量。设此时的最大弯曲应变为a′。

假设a′=a+a0cosnγt，则此时弯曲应变：

式中：a0cosnγtcosθt为高阶简谐变化量，频率与轴系转动频率不相同。它是由轴系转动中的激振力引起的[4]。由于应变具有如此规律，因此可以利用信号的滤波技术消除部分应变跳值和某些影响振动的因素。

本节考虑的弯矩都只沿垂直方向作用，即最大弯曲应变位于截面垂向最高点。但在轴系调整阶段，轴系存在水平方向的弯矩分量，且最大应变位置不在垂向最高点。因此，为了求得轴系实际负荷情况，必须对截面最大弯曲应变及其位置进行分析。

1.2 最大弯曲应变及其位置分析

如图3所示，设最大应变方位角为δ，则此时截面处的弯曲应变分布为

式中有两个未知数，最大弯曲应变a和方位角δ，只要用两组应变采集点信息就可以解出。传统应变片法的实质正是如此，通过90°和180°或270°和360°两组测点来计算。这种方法由于参与计算的测点较少，因此误差较大。本文由于分析出了截面弯曲应变分布规律，可以采用多测点参与计算。

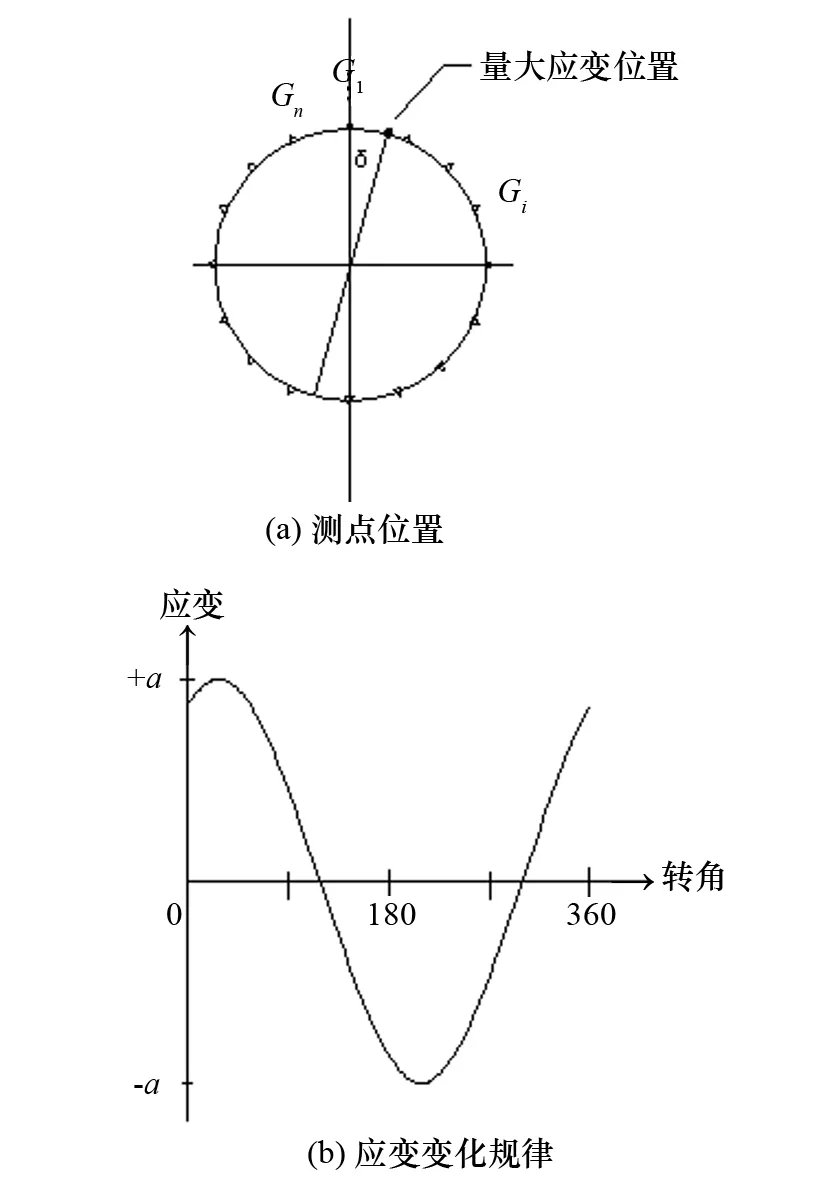
图3 应变采集点位置及应变变化规律

假设应变仪采样的频率Fs，轴系转速为N(r/s)，且保证Fs/N为整数。则每圈采集点数为n=Fs/N。因为转速是恒定的，所以应变采集点是等间隔的，相邻两采集点间的夹角为

设0°角为起始标定位置，则任意转动位置Gi到起始点G1的角度为

又由式(5)知，任意转动位置Gi处的应变为

为了得到所有采集点的应变数据，将式(8)左右两端取平方和，得

对式(9)利用三角函数倍角公式化简，得

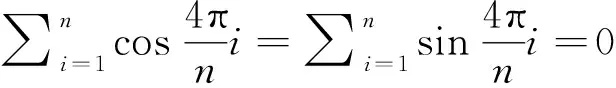
由此，可以利用轴系转动一圈的应变值来求出最大应变。而相应的最大应变对应的方位角为

式中的正负号视实际情况而定。

1.3 扭转应变对测量轴系弯曲应变的影响

由于轴系转动时会产生一定的扭矩影响。因扭转产生的切应变会对弯曲应变的采集产生影响。必须通过适当手段剔除切应变的影响。

应变片与被测物贴合在一起，可以与被测物一起伸缩，在伸缩过程中应变片的阻值会发生变化。一般电阻的变化率为常数，电阻的变化与应变成正比，其关系式如式(13)所示。将应变片接入桥路中，通过测量桥路电压的变化来间接测量被测物的应变情况[5]。

式中，R为应变片原电阻值；ΔR为应变片伸缩后电阻的变化值；K为应变片的比例常数；ε为应变。

测量轴系转动时的弯曲应变，采用如图4所示的半桥连接法，图中R1和R2位于相邻桥臂，设弯矩为M，扭矩为T。在弯矩M作用下，传动轴发生弯曲变形，上表面受到拉伸，下表面受压缩，故R1和R2处的应变正好相反，产生的电阻变化量分别为ΔRM和-ΔRM，测量桥路的不平衡输出电压：

在扭矩T作用下，轴产生扭转变形，R1和R2处应变都相同，产生的电阻变化量均为ΔRT，此时UBD=0。由此可看出UBD完全是由弯曲变形引起的[5]。故采用半桥接入法的确可以消除由扭矩对弯曲应变产生的影响。

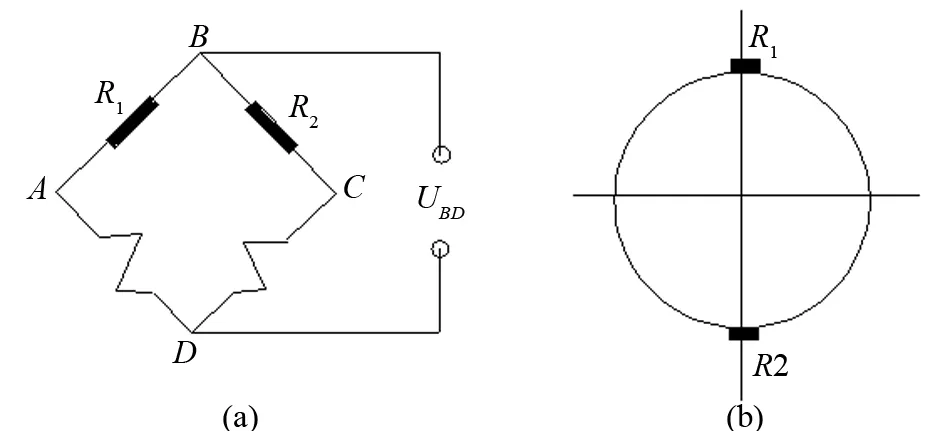
图4 半桥接线法示意图

2 轴承负荷计算

2.1 截面弯矩计算

在得到最大应变a和其方位角δ后，考虑到实际测量中的一些修正，可以计算得到测点处的弯曲应力和弯矩。

弯曲应力：

弯曲力矩：

或

式中：a为最大应变、δ为最大应变方位角、W为轴段的抗弯截面系数、E为轴的弹性模量、β为线路修正系数、C为桥臂系数。Mx、Mz为作用在轴截面弯矩的垂直分量和水平分量。

2.2 尾轴段轴承负荷计算

得到轴截面弯矩后，将轴系按测点截面分割成若干轴段，轴段上的载荷可以通过校中书得到。在每轴段内建立垂直和水平方向的力和力矩平衡方程，求得轴承处的实际负荷。中间轴承段计算与以往的应变片法计算类似，按上述流程进行。尾轴段计算模型，可分为两种：单支点计算模型和双支点计算模型。由于这两种方法相似，下面以单支点计算模型为例作简要分析。

图5为单支点计算模型示意图，图中P1、P2为螺旋桨和法兰的集中载荷，Q1为Q6轴段重量。所谓单支点就是将后艉轴承的支撑力假设汇聚到一点，设支点(O)距轴承后端点A的距离是x′。艉轴应变片一组在C处，位于法兰前x1处，另一组在D处，距离中间轴承后端x2处。通过这两组片，测得贴片处的弯曲应变，进而算出所在截面的弯矩，通过弯矩和力的平衡方程，就可以计算出后尾轴承的支撑点位置和支反力。

图5 艉轴段受力图(单支点)

垂直支撑力：

水平支撑力：

支点位置：

3 算例

根据上述基于应变波形的船舶推进轴系负荷测量方法，对国内某18万吨散货船进行测量。本船轴系由两个轴段组成，中间通过法兰连接。有一个中间轴承，一个艉管前轴承，一个艉管后轴承，一个主机端轴承。

图6为应变片位置布置图。本实验需要测量艉管前后轴承以及中间轴承的负荷。故应变片布置如下：1号片位于靠近艉轴管壁的右侧，2号片位于法兰与中间轴承之间，距中间轴承70 mm～200 mm

[][]

处(一般贴在中间轴承处轴肩以下)，3号片位于中间轴承右侧，4号片处于中间轴承与主机端轴承中间位置。

图6 应变片布置图

试验通过两种方法测量轴承负荷，其中第一种是使用自带应变采集功能的应变仪采集应变信号，通过本文介绍的基于应变波形不间断测量法计算出的轴系负荷数据；第二种是通过传统间断应变测量方法测得的轴系负荷数据。同时参照某国际权威机构的顶举法数据，表1为负荷的对比情况。

表1 负荷汇总表

4 结论

船舶轴系负荷测试是轴系校中的重要依据，它对维持轴系长期正常运转有着不可替代的意义。基于应变片法的基本原理，结合弯曲应变波形规律，改进了应变片测量轴系负荷的方法。通过上述测量实验结果，可知三种测量方法测出的负荷差距都很小。证明了本文提出的基于应变波形的应变片法测量轴承负荷的可行性。它比过去的方法测量更简便。

船舶轴系在运转过程中轴承受到的负荷与静止状态时不同。传统应变片法和顶举法测量的是轴系静态负荷，无法测量轴系的动态负荷。而本文基于波形的负荷测量方法，为动态负荷测量提供了一种思路。在该测试方法下，如将应变仪改进为无线应变仪，则可以对轴系动态负荷进行初步测量。

[1] 周继良,邹鸿钧.船舶轴系校中原理及其应用[M].北京：人民交通出版社，1985.

[2] 曲智. 船舶推进轴系负荷测试系统开发[D]. 大连:大连理工大学, 2013.

[3] Batra A, Shankar K, Swarnamani S. Propulsion shaft alignment measurements on warships afloat and alignment solution using multi-objective optimisation[J]. Proceedings of the Institute of Marine Engineering Science & Technology Part A Journal of Marine Engineering & Technology, 2007(9):39-49.

[4] 陈泽智, 陈明, 王传溥,等. 船舶轴系动态弯曲应变的测量与分析[J]. 船海工程, 2000(3):13-15.

[5] 赵巍, 张永珍. 电阻应变计法测量组合变形轴的扭矩和弯矩[J]. 唐山学院学报, 2009(3):1-2.

Research on the Measurement of Ship Propulsion Shafting Load Based on Strain Wave Method

WANG Ji1,2， FAN Rong1， LI Rui1， LIU Yu-jun1， WANG Shi-yuan3

(1. State Key Laboratory of Structural Analysis of Industrial Equipment，Dalian Liaoning 116024， China； 2.Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration(CISSE), Shanghai 200240, China；3.BlueCross BlueShield of Tennessee, Chattanooga Tennessee 37402， USA)

The resistance strain gauge method is widely applied in load measurement of marine propulsion shafting. However, traditional resistance strain gauge method is complicated to measure the data which can only be collected when shafting rotation is stopped. Besides, the number of measuring point is very limited which is likely to cause a big error. In this paper, an improved resistance strain gauge method was proposed which can avoid the stopping of shafting rotation during the measurement. The strain wave of shaft in low rotation speed was analyzed after the complete strain wave had been collected by strain indicator so that the error points could be filtered out and the maximum strain and the bending moment of shaft cross section and could be deduced. Finally, the bearing load distribution was calculated with the balance equations of force and moment. The feasibility of the measurement method was verified by the collection and calculation of subsistent vessel data.

Strain gauge method Shaft alignment Strain wave shape curve Bearing load

辽宁省高等学校创新团队项目(编号：LT2014002)资助。

汪 骥(1978-)，男，副教授，博士，主要研究方向为船舶与海洋结构物先进制造与管理技术。

U664

A