地震救援中基于信息实时更新的两阶段应急物资调配模型
2016-12-28刘舒悦朱建明孙军红
刘舒悦,朱建明,黄 钧,孙军红
(1.中国科学院大学工程科学学院,北京 100049;2.首都师范大学数学科学学院,北京 100048)
地震救援中基于信息实时更新的两阶段应急物资调配模型
刘舒悦1,朱建明1,黄 钧1,孙军红2
(1.中国科学院大学工程科学学院,北京 100049;2.首都师范大学数学科学学院,北京 100048)
应急物资调配是应急管理中一个重要的课题,准确、高效的应急物资调配方案是决定应急救援的成功的关键,然而应急情况下信息的不确定性增加了物资调配问题的难度。本文以应急物资调配的不确定性处理作为重点,研究地震发生后的应急物资调配方案。本文将应急救援过程按灾情信息获知程度分为黑箱期(仅知道震级、震中的时期)与灰箱期(各地震害指数依次更新的时期)。黑箱期根据历史地震灾情数据得到相应的离散情景集,并基于此使用鲁棒规划建模。在灰箱期阶段,本文根据震害指数更新烈度圈及各受灾点的物资需求,计算未满足率,从而决定是否进行新一次的配送,使用数学规划求解配送方案。最后,本文以鲁甸地震的实际数据为例进行分析验证了模型的有效性。
信息更新;两阶段调配;情景分析;鲁棒规划;烈度圈实时更新;多次调配
1 引言
物资调配是应急救援中一个重要的环节。应急情况下的物资调配具有突发性、紧迫性、多样性、巨量性、不确定性等特点[1]。突发性是指自然灾害发生的突然且部分不可预测;紧迫性是指为了保障灾民的生命,需要及时调配;巨量性是指物资的数量要足以保证一个区域的灾民一段时间的生活,常以千、万为单位;不确定性是指灾害发生后一段时间,不同种类的灾民人数未知,物资需求量未知;多样性是指物资需求多样,《应急保障重点物资分类目录》[2]将应急物资分为三大类,若干小类,不同物资的调配时机与需求量也不同。这些特点决定了应急救援模型的特征:配送时效高、物资种类多、物资数量大、充分考虑不确定因素等。
已有的应急物资配送模型各有侧重:多目标规划模型侧重于研究不同的目标选择,如配送时间、设施成本、灾民满意度等对模型结果的影响;分阶段的模型侧重于研究配送空间(两级、多级运输网络)或时间的划分对模型结果的影响;包含不确定信息的模型,如鲁棒模型、随机规划模型、模糊规划模型等侧重于研究如何刻画救援中的不确定信息,使救援结果能最大程度贴近实际情况;智能算法模型侧重于研究特定算法对于应急物资调配问题求解结果的影响,普遍研究的算法如粒子群算法、遗传算法等。本文侧重于研究应急调配中不确定信息的更新对调配的影响,包括对灾情信息的描述以及灾情信息变化的描述。现有研究中,大多选取震害指数、受灾烈度、受灾人数等作为灾情信息,灾情信息大多以概率或情景方式表出,灾情信息的更新表现为概率或情景的变化。本文选取多个因素组成情景来描述灾情信息,信息变化的描述表现为因素概率变化的描述。本文的意义在于,既有研究当中,灾情信息的变化大多采用生成模式,而本文中信息的更新是从实际数据提取的结果。
本文共分为6个部分,第1部分描述应急物资调配问题及其背景;第2部分是关于应急物资调配的综述,从研究方法、阶段划分、目标选择三个部分阐述了现在的研究概况;第3部分是模型的建立与描述;第4部分阐述模型求解的方法;第5部分是算例分析以及模型比较;最后第6部分得出本文的结论。
2 应急物资调配研究概况
应急物资调度的研究方法主要包括数学规划[3]、概率统计[4]、仿真、博弈论[5]、排队论、模糊理论、随机规划[6]、系统动力学、约束规划等[7]。王晶[3]用双层规划建立了省、市、县三级的物资储备模型。Liu Nan和Ye Yong[4]用概率描述灾情,建立了贝叶斯模型。庞海云和刘南[5]提出了不完全满足应急需求的策略,将问题求解分为两个阶段用博弈论模型的鞍点准则求解。詹沙磊和刘南[6]建立多目标随机规划的物资调配模型,以贝叶斯风险作为目标函数。
常见的应急物资调配的目标为:最小化时间成本、最小化费用成本、最小化物资未满足率等。应急物资调度的研究,按阶段划分,可分为单阶段与多阶段的。单阶段类的文献把应急响应整体作为一个阶段,进行单次调配,如刘明和赵林度[8]建立的混合协同配送模型,张玲建立的鲁棒规划模型[9]。物资的多阶段调配中的阶段划分,有的根据学者提出的救援时期的划分而来,如黑箱期、灰箱期,或准备、响应、混合[7];有的模型本身存在阶段划分,如GuoPengfei和Liu Fang[10]等用幸存者函数拟合需求变化,根据车辆的动态到达划分阶段,实现物资的动态调度。
传统的应急物资调度模型鲜少考虑到灾情信息的更新。现实中,灾情发生后,灾情信息随着时间推移逐渐明朗,信息发布形式包括媒体曝光、政府发布、相关人员发布微博等。近年来,已有学者注意到信息更新对于提高调配决策准确性的重要程度。葛洪磊[11]考虑了信息更新在决策中的应用,定义了全局灾情信息的观测序列。即定义全局的灾情信息θ(整体的房屋倒塌率),对灾情进行p次观测得到灾情序列θ1,θ2,…,θp,在此基础上进行调配决策。Liu Nan和Ye Yong[4]用概率反应灾情信息,用贝叶斯条件概率作为更新后的灾情信息,建立了贝叶斯模型。
然而以上模型考虑的信息更新与实际地震发生时更新的信息有较大差别。现实中更新的信息主要包括各地的震害指数、死亡人数、受伤人数等,而没有上述文献提到的灾情发生的概率。本文考察了现实中信息更新的流程,提出一个切合实际的调配-调整的动态实时决策模型。
3 烈度圈更新下的两阶段应急物资调配鲁棒模型
本文研究地震发生后的物资调配及设施选址问题,将调配过程分为两个阶段:无灾情信息更新的阶段(黑箱期)和有灾情信息更新的阶段(灰箱期),在黑箱期使用历史数据生成情景,此步可使用聚类方法适当减少情景已简化计算,并用鲁棒模型求解物资调配及选址方案;在灰箱期通过各地震害指数更新来更新的烈度圈,从而更新物资需求数量,计算物资未满足率,最后使用数学规划决定调配方案。
3.1 黑箱期模型
“黑箱期”一般为地震发生后的1~2天,在此期间内,决策者只能知道有关地震的初级信息:震级、震中。在此阶段内,决策者只能根据仅有的信息及历史数据进行紧急调配。此阶段完成两个任务:1.情景生成。本文将一次历史地震信息整理成一条记录或一条情景,一条记录或情景是一个多维向量,向量中的每个元素称为要素。获得历史记录或情景的过程称为情景生成。其中,因为部分情景要素不容易通过查询获得,所以定义了记录的概念,记录的要素相对容易获得,通过对记录要素做线性变化可得到情景要素。情景要素的震中受灾比例、震中道路损毁率,最终通过衰减率转化成各地受灾比例、各地道路损毁率,反映到鲁棒规划模型中。2.鲁棒规划。根据情建立鲁棒规划模型,将受灾比例转化为物资需求,道路损毁率转化为交通成本,结合集散中心建设成本,建立多目标的鲁棒规划模型,给出初步的集散中心选址及物资分配方案。
3.1.1 情景分析
情景分析假设:
1.某次地震中各受灾点的受灾比例与道路损坏率根据震中距按衰减率线性递减,两者衰减率相同
2.道路损坏率、受灾比例与震级成正相关,与震中距正相关
3.各地受灾比例从震中开始按衰减率线性衰减
4.各地道路受损率从震中开始按衰减率线性衰减
一次历史地震对应一条记录或情景,定义记录是为了将其通过线性变换转化成情景。其中,平均(震中)受灾比例为:政府公布的总(震中)受灾人数/总受灾点(震中)人口总数。平均(震中)道路受损率为:总(震中)损坏道路受损的公里数/总(震中)的所有道路的公里数。受灾范围为政府公布的受灾点数量,以县(区)为统计单位。在历史记录的选取上,主要选取地震发生地类似震级数据。例如若需要计算雅安7级地震的物资调配方案,则选取历年四川地区7级左右地震的数据。情景生成的步骤如下:1.查询地震信息得到震级、震中受灾比例、受灾范围。2.生成衰减率。生成衰减率有两种方法,当该地震各受灾点的受灾比例都能查询到,则使用方法一:拟合,用最小二乘法根据各地受灾比例及各地震中距拟合出衰减率;否则使用方法二:插值,查询某地或平均的受灾比例(得到记录要素),根据转化方程一求得衰减率。3.生成道路损毁率。首先查询该次地震的震中道路损毁率;若查不到,则查询平均(某地)的道路损毁率,结合衰减率根据方程二插值出震中道路损毁率;若仍查不到上述信息,则假设平均道路损毁率是震级的线性函数,查询同地区其他地震的数据,拟合出震级与道路损毁率的函数关系,再将该次地震的震级代入,求得平均道路损毁率。最后,考虑到计算过程的复杂性,可使用聚类方法减少记录/情景数量,简化计算。
3.1.2 鲁棒规划模型
鲁棒规划模型假设:
1.物资流方向为储备库—>集散中心—>受灾点,各层级内部(储备库之间、集散中心之间、受灾点之间)无物资流动。
2.两点间的交通距离为两点间最短路


xlija第l次更新时物资储备库i到集散中心j的a类物资的配送数量yljka第l次更新时集散中心j到受灾点k的a类物资的配送数量plij第l次更新时是否选择i点对j点配送qljk第l次更新时是否选择j点对k点配送zj是否在j点建立集散中心

l=0
(20)
其中:(1)为目标函数,目标是最小化未满足成本、各点间距离成本及选址成本;(2)是各地受灾比例的计算;(3)和(4)是各地道路损毁率的计算;(5)为j点的选址成本,公式为仓库面积×单位房租;(6)为情景ω下受灾点k对物资a的需求量计算方法,函数fa引用自其他文献;(7)表示受灾点k缺乏物资a的惩罚系数;(8)表示储备库i发出物资a的总和要小于该点物资a的储备量;(9)表示集散中心j发出的物资a的数量要小于储备库运送到该点的数量;(10)表示运送到集散中心j的物资的总体积要小于该点容量;(11)表示受灾点k分配到的a类物资要小于该地所有情景下需要的最大物资;(12)表示道路(i,j)上运送的物资总量要小于该路段的容量;(13)表示道路(j,k)上运送的物资总量要小于该路段的容量;(14)、(15)表示若选择某段道路进行运输,则其运送量要大于0;(16)、(17)表示若选择j点作为集散中心,则该点进行物资配送;(16)、(17)表示决策变量的取值范围。(20)表示黑箱期配送中l=0。该模型可化成线性规划模型,使用CPLEX求解。
3.2 灰箱期模型
灰箱期的物资调配可视为对前一阶段调配结果的调整。当灾情信息开始更新后,地震救援进入“灰箱期”。本文的选取各地震害指数(即房屋倒塌率)作为灾情信息。地震发生后,可用经验公式求得初始烈度圈,此时的烈度圈与真实情况有较大偏差,但烈度圈可以随着各地震害指数的更新而更新[13]。这一更新的现实意义在于,各地震害指数的更新情况可从政府发布的新闻中得知。由此,每更新一个地区的震害指数,便能得到一个当前情况下与实际最相符的新烈度圈。根据烈度圈与受灾比例的对应[14],各地的受灾比例也相应更新,由此我们得到新的物资需求量。定义未满足率,若未满足率达到一定标准,就可使用确定的数学规划求解调配方案。此时不在烈度圈中但在黑箱期收到物资的受灾点,作为新的出救点加入到网络中。
3.2.1 烈度圈更新
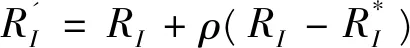
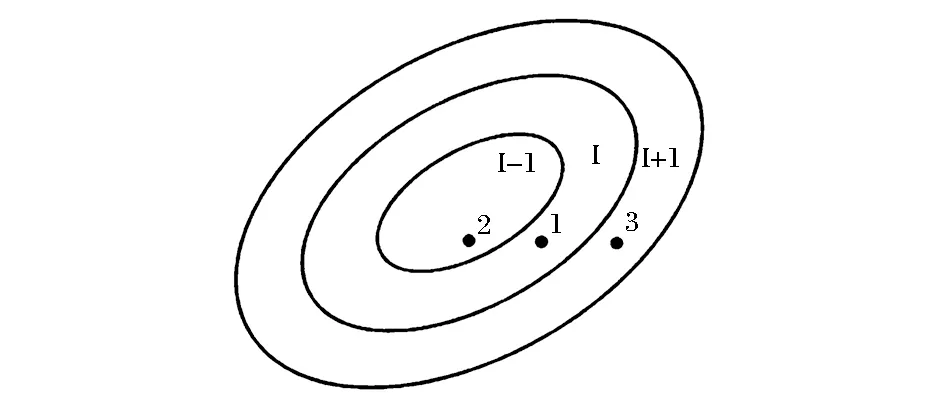
3.2.2 灰箱期物资调配模型
模型假设:
1.前l次更新都不在烈度圈内的受灾点,作为第l次更新时的集散中心候选点
2.第l次更新时,任一物资未满足率>0的点作为受灾点
3.不低于1/4的受灾点的任一项未满足率超过10%,则进行配送。(假设3的标准需要由专家制定。)
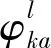
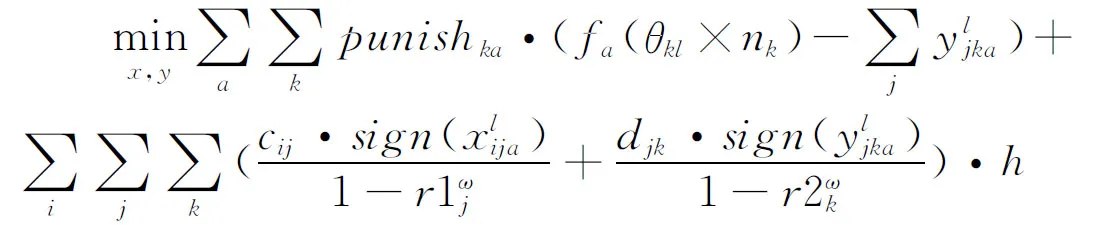
(18)
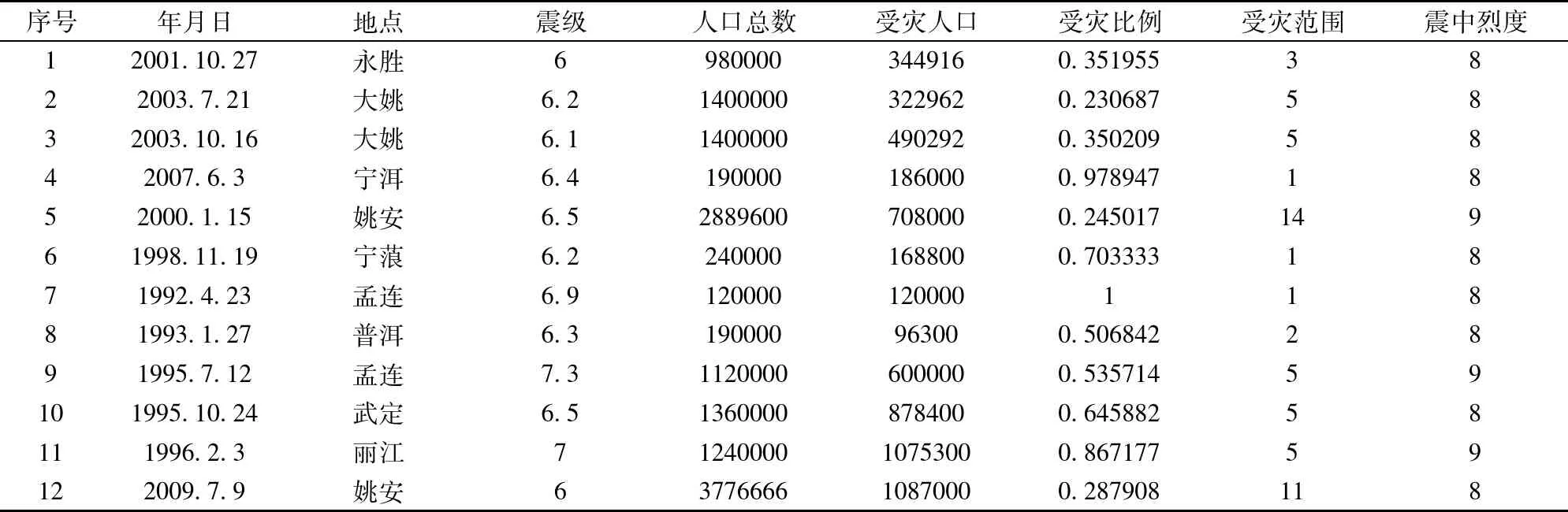
表1 历史地震部分信息(数据来自中国地震局官网)
s.t.
(19)

(20)
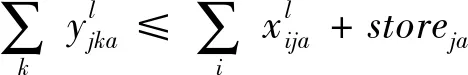
(21)
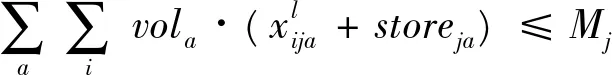
(22)

(23)
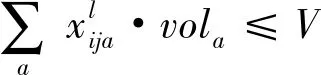
(24)
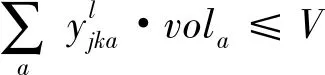
(25)
(26)
其中:(18)表示目标为最小化未满足成本与配送距离成本;(19)表示集散中心j现有的物资存储量为前一阶段的收到的配送量-该点发出的量,其中;(20)表示储备库i发出物资a的总和要小于该点物资a的储备量;(21)表示集散中心j物资a的发出量要小于该点储备量与收到的配送量的总和;(22)表示集散中心j的物资总体积要小于该点的容量;(23)表示受灾点k收到的物资a的数量要小于该点当时的需求量;(24)(25)是道路容量限制;(26)是决策变量取值范围。
4 算例分析
以2013.8.3云南鲁甸6.5级地震为例。2014年8月3日16时30分在云南省昭通市鲁甸县(北纬27.1度,东经103.3度)发生6.5级地震,震源深度12千米,余震1335次。此次地震灾区最高烈度为 Ⅸ度,等震线长轴总体呈北北西走向,Ⅵ度区及以上总面积为10350平方千米。本文假设此次救援行动为省级联合救援。
4.1 黑箱期模型计算
4.1.1 情景分析
在数据采集过程中,发现道路损毁率的信息较难得到,因此不能直接通过查询数据得到情景要素信息,需要从记录要素转换。因此,本案例情景分析的计算步骤为:1.生成记录;2.通过聚类减少记录数量;3.将记录转换为情景。为保证数据的适用性,本文将只统计案例所在地(西南)的历史地震信息。详细步骤及信息如下:
1.生成记录
1)查询历史地震震级、受灾比例、受灾范围

表2 震级与道路损毁率数值
2)插值计算道路损坏率
查询到芦山及汶川地震的道路损毁率[16],用插值方法计算震级与道路损毁率的线性函数,用此线性函数补全记录中缺失的信息。其中,芦山地震的历史信息按原文文意,损毁率高为基本不通行,中为基本通行,一般为通行,低为完全通行。将完全通行换算为不通行概率100%,则高对应100%,中对应75%。“通行”及以上情况视作正常情况,“基本通行”及以下状况视为地震引起的异常。令该地的总道路损毁率=(不通行道路长+基本通行道路长×75%)/总路长,则得出总道路损毁率=29.12%。第二个数据,汶川地震的道路损毁率[15],取其总体平均值,结果为38.64%。于是我们得到同地区震级与道路损坏率对应的两个数据(表3)。通过插值得到函数y=9.5119x-37.459,其中x为震级,y为平均道路损坏率。
3)综合上述结果生成记录

表3 历史地震信息记录
2.聚类
为简化计算,同时保证每条记录的信息能得到充分利用,将结果依据最远距离使用层次聚类,并按height=4剪枝,并计算各类均值为各类的属性值,则得到典型记录:
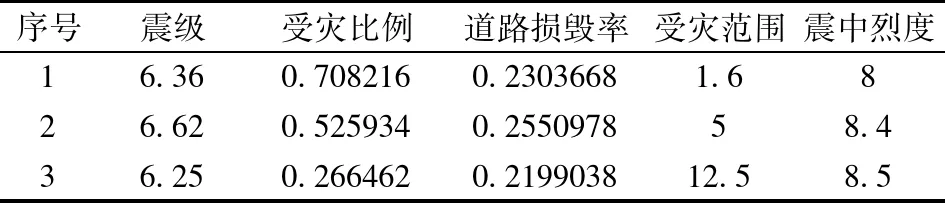
表4 记录聚类后
3. 生成情景
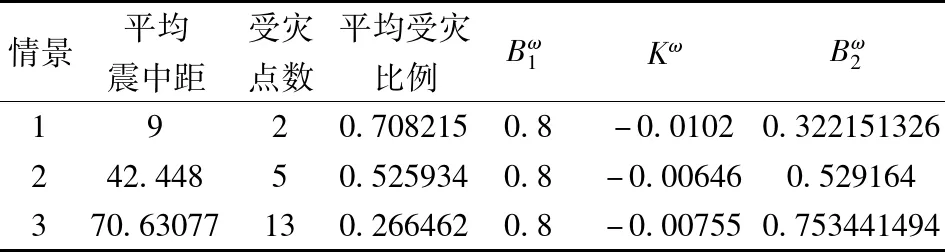
表5 各情景下受灾比例回归函数参数
2)得到情景
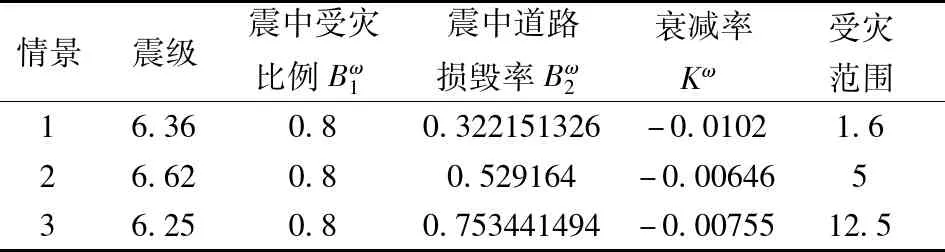
表6 情景集
4.1.2 黑箱期鲁棒模型计算
设出救点为联合物资储备企业及地方物资储备中心。出救点、集散中心候选点选取及序号对应如表10. 受灾点个数根据情景生成,最多有12.5个,我们先选定地图上离震中最近的13个县(市),分别是:鲁甸县、大关县、彝良县、昭阳区、会泽县、昭觉县、金阳县、布拖县、普格县、宁南县、巧家县、会理县、会东县;在情景2中,只选距离最近的5个点作为非零需求的受灾点:鲁甸县、巧家县、金阳县、宁南县、昭阳区,其他为零需求受灾点;在情景1中,非零需求的受灾点为鲁甸县、巧家县。

表7 出救点和集散中心候选点位置
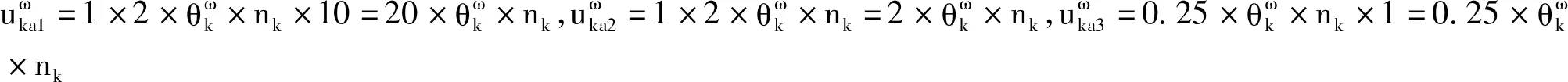
计算结果选定五个集散中心,分别位于寻甸(2)、宣威(4)、武定(5)、凉山(8)、泸州(11),调配方案如下:(储备库至集散中心)昆明至寻甸:水500万瓶,粮食54.54斤,帐篷8万顶;曲靖至宣威:水200万瓶,帐篷3万顶;楚雄至武定:水200万瓶,帐篷3万顶;保山至武定:水200万瓶,粮食30万斤,帐篷1.89万顶;临沧至武定:水200万瓶,粮食30万斤,帐篷3万顶;景洪至武定:水200万瓶,粮食30万斤,帐篷3万顶;成都至宣威:水200万瓶,粮食77.21万斤,帐篷6.65万顶;凉山至凉山:水200万瓶,粮食30万斤,帐篷3万顶;泸州至泸州:水200万瓶,粮食30万斤,帐篷3万顶;阿坝至凉山:水200万瓶,粮食14.46万斤,帐篷3万顶;巴中至泸州:水200万瓶,粮食29.49万斤,帐篷3万顶。(集散中心至受灾点)寻甸至会泽:水500万瓶,粮食54.6万斤,帐篷6.83万顶;宣威至鲁甸:水619.3万瓶,粮食61.93万斤,帐篷7.742万顶;宣威至彝良:水80.7万瓶,粮食15.3万斤,帐篷1.91万顶;武定至巧家:水752万瓶,粮食75.2万斤,帐篷9.4万顶;武定至会东:水47.8万瓶,粮食11.9万斤,招聘1.49万顶;凉山至金阳:水77.35万瓶,粮食12.2万斤,帐篷1.525万顶;凉山至布拖:水92.3万瓶,粮食9.23万斤,招聘1.15万顶;凉山值宁南:水156.7万瓶,粮食15.67万斤,帐篷1.9587万顶;凉山至会理:水73.6万瓶,粮食7.36万斤,帐篷0.92万顶;泸州至昭阳:水400万瓶,粮食59.489万斤帐篷6万顶。
4.2 灰箱期模型计算
灰箱期首先给出初始烈度圈及震害指数更新表(表10),根据表10依次更新烈度圈,再根据更新后的烈度圈计算物资需求及未满足率,若未满足率达到标准则进行下一次配送。其中,表8包括震害指数更新的顺序及震害指数。前6个数据来源于中国地震局官网播报。初始烈度圈的给出见参范一大等[14](表9)。
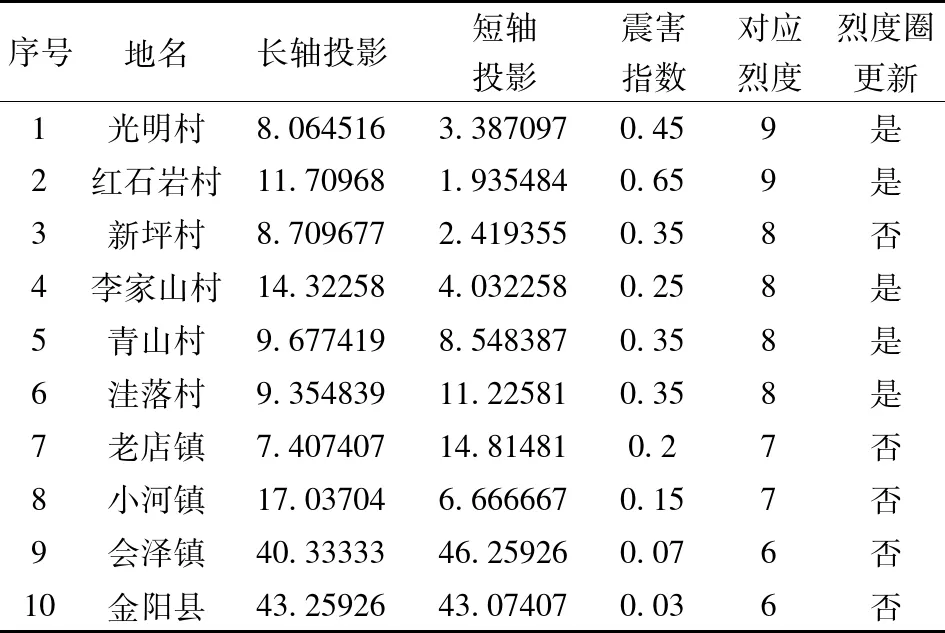
表8 震害指数更新次序

表9 初始烈度圈
4.2.1 第一次更新时的计算
1. 烈度圈更新:
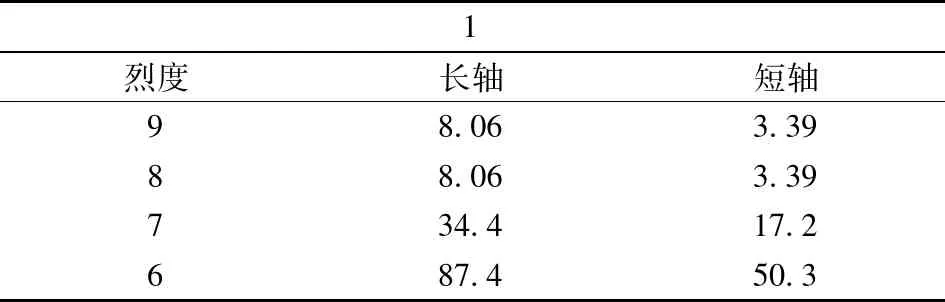
表10 第一次更新后的烈度圈
2. 根据更新的烈度圈,计算受灾比例,烈度与受灾比例的对应见范一大等[14],如表11所示:
4. 决定是否配送
根据假设决定进行配送。此次配送中,彝良、会理、会东作为新的集散中心增加到集散中心候选集,受灾点集为鲁甸、昭阳。根据模型,计算结果如下:
4.2.2 后续更新计算
经计算,2-11次信息更新都无需配送。详细计算信息如下:
1.烈度圈更新过程见表14。
2.受灾点烈度更新后,有变动的未满足率更新如表15。
4.3 算例分析与模型比较
与实际结果相比,模型给出的调配方案覆盖了大部分受灾点,少数没有被覆盖的受灾点(毕节、会东)是边界受灾,根据其震中距不在情景给出的受灾范围内。据此,模型的一个改进方向是调整距离的计算。
将本文模型与没有信息更新的模型进行对比。选择张玲等[9]构建的基于三级运输网络的最大最小后悔值鲁棒模型(相对鲁棒模型)作为对比模型,使用同一算例作为模型输入,将两个模型的输出结果整理如表16。
通过对比可以看出:1)本文模型覆盖的受灾区域较广。根据实际数据,鲁甸地震的实际受灾点为鲁甸、昭阳、会泽、金阳、布拖、宁南、巧家、会东。本文模型覆盖了除会东外的所有受灾点;而对比模型在水的供应上没有覆盖到会泽、宁南、会东三个受灾点,在其他两个物资的供应上没有覆盖到会东。2)本文模型配送的精度较高。本文模型中所有非受灾点都未收到物资,而对比模型中,非受灾点昭觉收到了配送物资。这是由于本文模型充分利用了信息的更新,借由新的信息对调配做出调整,从而很好的避免了物资浪费。由此可见,本文模型有更高的物资利用率。2)对于大部分灾区及物资,本文模型给出的供应数量大于对比模型给出的供应数量。这是由于本文的决策是基于一个更保守的策略,充分考虑了最坏情境,因此结果显现出很好的稳健性;而对比模型是一个基于后悔值的模型,目标是配送误差不能太大,结果具有更好的灵活性。但从以人为本的角度看,本文模型的结果优于对比模型的结果。

表11 首次更新后的各受灾点烈度判定

表12 首次更新后的各受灾点未满足率
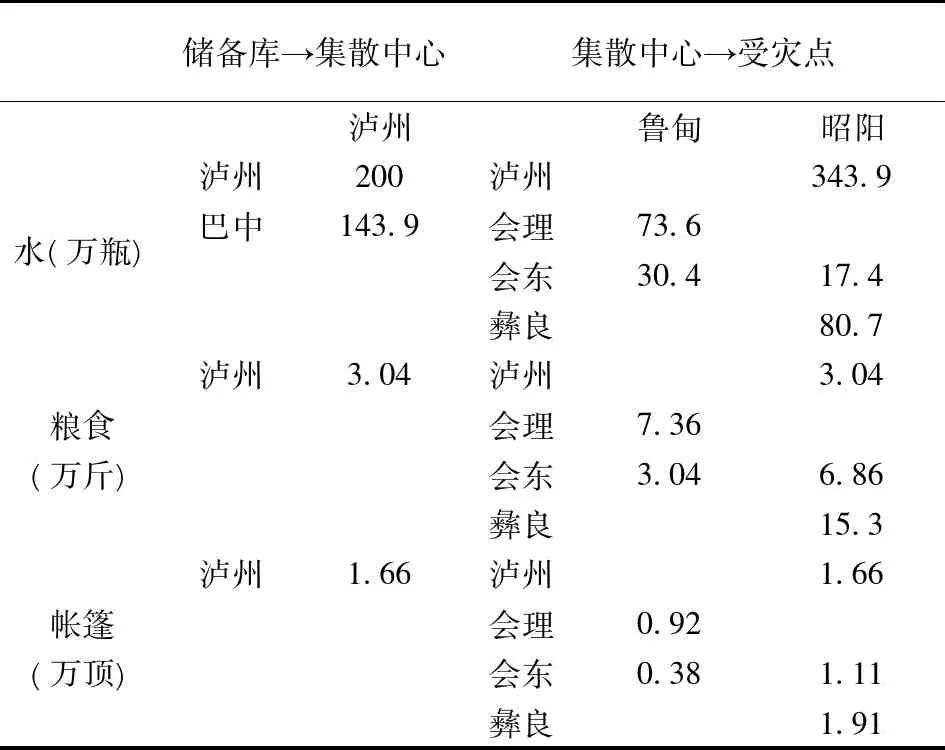
表13 首次更新后的调配方案
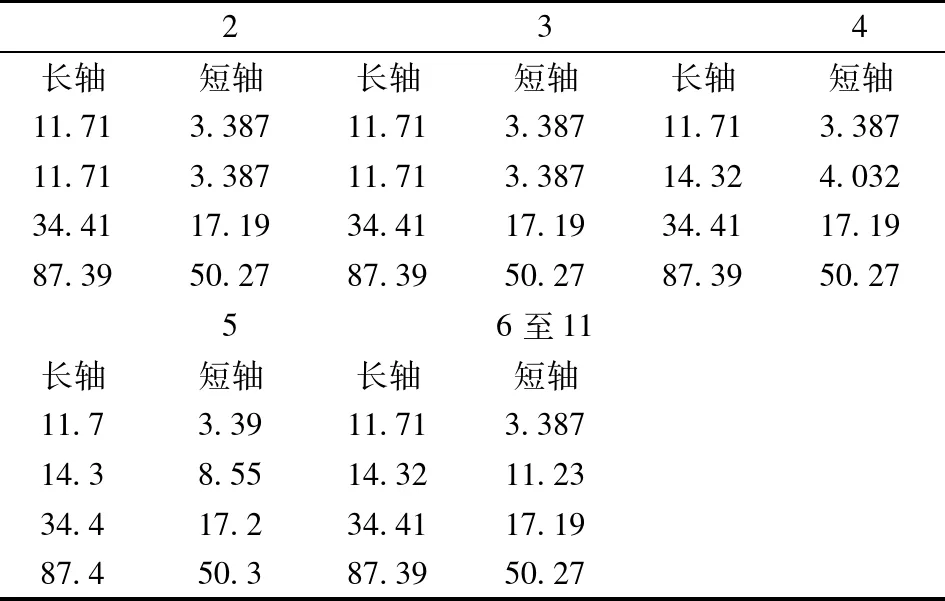
表14 2-10次烈度圈更新
5 结语
本文提出了一种实时动态的调配方案,在灾情信息未知时使用鲁棒模型进行保守调配;灾情信息更新后根据信息的更新对物资需求进行更新,从而保证实时满足灾区物资需求。此调配方案最大限度的考虑了实际情况,能够实际的反应灾情变化。求解方面通过引进新变量、增加新约束,简化了初始模型以及求解过程。同时,考虑了首次调配决策的后效性,灰箱期的调配决策可视为对前一阶段调配的调整,整体调配过程是一个不断完善、不断贴近实际需求的过程,对减少人民生命财产损失具有重要意义。
同时,本文可以改进的地方是:1.可用程序实现情景生成,如此可生成更多的历史数据,有助于完善鲁棒模型。2.第二阶段的阈值确定还不够完善,可通过参数实验或专家调研得出。

表15 各受灾点未满足率更新
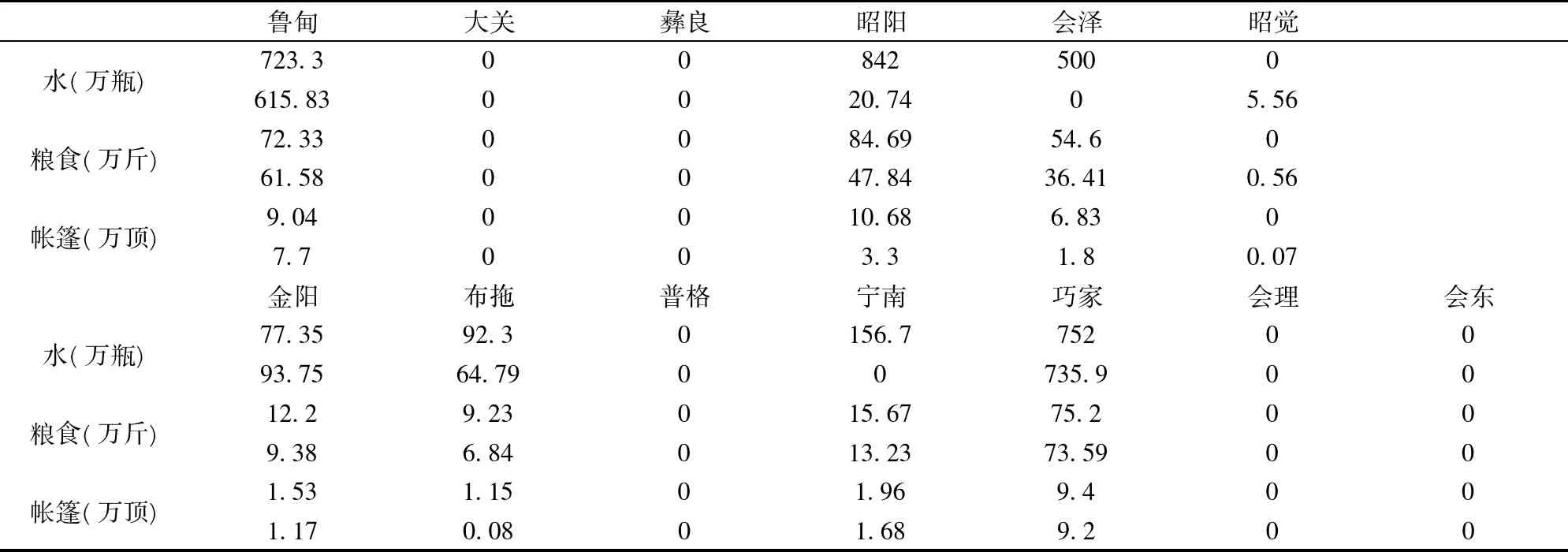
表16 各受灾点所收物资
[1] 唐凤,朱建明,王晶,等.非常规突发事件应急物资需求分析研究[C]. 第四届国际应急管理论坛暨中国(双法)应急管理专业委员会第五届年会,北京, 12月12日-23日,2009.
[2] 中华人民共和国国家发展改革委员会.应急保障重点物资分类目录[S/OL].[2015-04-07].www.sdpc.gov.cn/zcfb/201504/t20150410-677159.html.
[3] 王晶,黄均,张玲.基于双层规划的应急资源布局模型和算法[C]. 中国控制与决策会议,桂林,6月17日-19日,2009.
[4] Liu Nan, Ye Yong. Humanitarian logistics planning for natural disaster response with bayesian information update[J]. Journal of industrial and management optimization, 2014,10(3):665-689.
[5] 庞海云,刘南. 基于不完全扑灭的应急物资分配博弈模型[J]. 浙江大学学报(工学版),2012, 46(11): 2068-2108.
[6] 詹沙磊,刘南. 基于灾情信息更新的应急物资配送多目标随机规划模型[J]. 系统工程理论与实践,2013, 33(1):159-166.
[7] Galindo G, Batta R. Review of recent developments in OR/MS research in disaster operations management[J]. European Journal of Operational Research,2013,230 (2) 201-211.
[8] 刘明,赵林度. 应急物资混合协同配送模式研究.控制与决策, 2011, 26 (1):96-100.
[9] 张玲, 陈涛,黄钧. 基于最大最小后悔值的应急救灾网络构建鲁棒优化模型与算法[J]. 中国管理科学. 2014,22(7):131-139.
[10] Guo Pengfei, Liu Fang. Optimal deployment of emergency supply inventory for the recurring disaster with a humanitarian relief objective[R]. Working Paper,SSRN, 2014.
[11] 葛洪磊. 基于灾情信息特征的应急物资分配决策模型研究[D]. 杭州:浙江大学, 2012.
[12] 高建国. 中国地震紧急救援理论研究 [J]. 华南地震, 2006, 26(1):118-125.
[13] 许卫晓,孙景江,林淋,等. 烈度快速评估中的实时修正方法研究[J]. 地震工程与工程震动, 2012,32(4):34-39.
[14] 范一大,杨思全,王磊,等. 汶川地震应急监测评估方法研究[J]. 遥感学报, 2008,12(6):858-864.
[15] 赵红蕊,王涛,石丽梅,等.芦山7.0级地震震后道路损毁风险评估方法研究[J]. 灾害学, 2014,29(2):33-37.
[16] 陈世荣,马海建,范一大,等. 基于高分辨率遥感影像的汶川地震道路损毁评估[J]. 遥感学报, 2008,12(6):949-955.
[17] 聂高众, 高建国,苏桂武,等. 地震应急救助需求的模型化处理[J]. 资源科学, 2001,23(1):69-76.
[18] 中国地震局地壳形变台网中心.中国地震烈度表[S/OL].[1999-04-26].www,dccdnc.ac.cn/html/zcfg/gfxwjz.jsp.
A Two-stage Operation Model for Emergency Management Based on Information Dynamic Updating In Earthquake Rescue
LIU Shu-yue1, ZHU Jian-ming1, HUANG Jun1,SUN Jun-hong2
(1.School of Engineering Science,University of Chinese Academy of Science,Beijing 100049,China;2.School of Mathematical Sciences,Capital Normal University, Beijing 100048,China)
Emergency supplies allocation is an important problem in emergency management. However, uncertain information of the disaster makes it hard to allot materials accurately and efficiently.In this paper, by focusing on the description and update of uncertain information, emergency supplies allocation strategy when earthquake occurs is studied. To describe the disaster, five factors are selected and different situations are constructed based on historical data. The information update process is described as the acknowledgement of the probability of each factor. Based on the updating of disaster information, the rescue process is divided into 2 stages: black stage and grey stage. In black stage, deciders only know magnitude and epicenter of this earthquake, therefore a robust model based on different situations is built. This model generates a robust result that considers the worst situation. Also, in this stage, historical information is used to generate situations to support robust model. In grey stage, damage index of each area updates successively, so that seismic intensity circle can be updated accordingly, and because of which, demand for each kind of material of each area can be updated. Then unsatisfying rate is computed, and a programming model is proposed for following supply allocation. Finally, by comparing our model against a model without information updating, experiment results show that our model has its advantages.
supplies allocation; two-stage model; robust model; Intensity circle dynamic update
2015-07-30;
2016-03-01
国家自然科学基金资助项目(91324012;91024031)
简介:朱建明(1979-),男(汉族),中国科学院大学工程科学学院副教授,研究方向:应急管理、运筹学、网络优化;E-mail: jmzhu@ucas.ac.cn.
O224
A
1003-207(2016)09-0124-09
10.16381/j.cnki.issn1003-207x.2016.09.015
