基于机器学习思想的非线性方程组求解

徐 林

(阳泉师范高等专科学校，山西 阳泉 045200)

基于机器学习思想的非线性方程组求解

徐 林

(阳泉师范高等专科学校，山西 阳泉 045200)

为解决非线性方程组求解过程中计算繁琐、计算耗时长、计算结果不精确的问题，选用机器学习方法，利用Bayes rules实现机器学习的决策操作和学习过程，融合半解析法的思想，开发非线性方程组实数/复数求解程序“GuessKey”，实现对非线性方程组所有的实数解和复数解进行搜索。同现在常用的非线性方程组求解算法进行比较，结果显示：该算法在全局搜索能力、计算精度、计算速度方面都优于其他算法。

Bayes rules；决策函数；半解析解；计算精度

1 研究背景

非线性方程组适合描述更为复杂的工程、自然现象，对于一些瞬变过程具有很好的适用性，是数学领域以及工程领域长期关注的问题[1]。但是，非线性方程组的求解过程比较繁琐，且没有解析解，一直为研究的难点[2-3]。

鉴于此，国内外学者针对拟牛顿算法进行了大量研究。Eisen等人[4]利用并行计算来提升计算速度，在计算时，可以同时利用不同的内核，从而使复杂非线性方程组求解问题成为可能，但Eisen等人并没有针对算法层面进行改进，依照的是计算机硬件的优势。Lorenzo Stella等人[5]利用粒子群算法-拟牛顿法求解非线性方程组，在一定程度上提升了算法的全局搜索能力，但仅限于实数解，对复数域没有涉及。Yousefian和Im ekli U等人[6-7]利用遗传算法-拟牛顿法求解非线性方程组，同样意在提升算法的全局搜索能力，但仅限于实数解，对复数域没有涉及。Farzad Rahpeymaii、Jun Kitagawa等人[8-9]通过对比不同的算法，发现机器学习在解答非线性方程组的时候，全局搜索能力颇佳，认为机器学习可以在复数域和实数域都有较好的全局搜索能力。

本文基于机器学习的思想，通过Bayes Rule实现机器学习的决策操作和主动学习过程，并融合半解析解的相关思想[10]，开发非线性方程组实数/复数求解程序“GuessKey”。利用机器学习对非线性方程进行学习，并运用学习后的数值空间对非线性方程进行求解，在得到一个非线性方程的半解析表达式之后，代入其他非线性方程，进而得到非线性方程组的解。最后，同常用的非线性方程组进行求解算法比较，在全局搜索能力、计算精度、计算速度3个层面揭示算法的适用性。

2 机器学习的基本思想

对于机器学习，将感兴趣的数据集合命名为D，集合D也被称为训练数据，机器学习的目标便是确定假设空间(命名为H)中的最佳假设。令P(h)表示未训练数据集合D之间假设h所拥有的初始概率，将其命名为prior probability。prior probability表示在当前知识背景之下，假设h为正确假设的概率。同理，令P(D)表示欲观察训练数据集合D的prior probability。P(D)反映在训练数据D之后假设h成立的置信度。

根据Bayes Rule：

(1)

在机器学习的过程中，考虑候选假设集合H，并从中寻找上述给定的数据集合D。在此，可能性最大的假设被命名为h(h∈H)，这样，具有最大可能性的假设被称为极大后检假设：

(2)

其中，hMAP被称为极大后检假设。联立式(1)和式(2)，得到

(3)

因为，P(D)并不是依赖于h的变量，而是一个常量，故而，式(3)可以写作

(4)

式(4)可以做进一步的简化，如果假定H中每个假设有相同的prior probability，就可以使用极大似然假设：

(5)

其中，hML被称为极大后检假设。对于H中的任意h，有

(6)

通过不断学习和训练，机器便拥有了对某一特定问题的处理能力。

3 非线性方程组求解

设非线性方程组

(7)

其中，(x1,x2,…,xn)为变量，(y1,y2,…,yn)为常数，为了便于书写，将式(7)记作

fi(X)=yi，i=1,2,…,n.

(8)

式中：

X=(x1,x2,…,xn)T.

(9)

令空间Ri表示第i个方程fi的自变量X的所有可能取值。假设X在空间Ri中的第k次抽样为

(10)

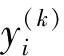
(11)

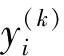
(12)

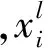
(13)

其中，δi被认为是Kmeans算法误差[11-12]。至此，便完成了对第i个方程fi的机器学习操作。

(14)

(15)

如此重复n次，得到

(16)

(17)

将式(16)代入式(7)，得到

(18)

如此共重复n次，可得X。

4 数值验算

通过上述理论，开发非线性方程组实数/复数求解程序“GuessKey”，为了验证本文算法A1的优越性，利用传统拟牛顿法A2、拟牛顿混合遗传算法A3、粒子群算法A4、NGEA算法A5进行比较。

4.1 全局搜索能力

(19)

利用数学知识可知，式(19)共6组解。利用5种算法分别进行计算，结果见图1。

根据图2，本文提出算法的搜索能力最强为A1，其次是NGEA算法A5、粒子群算法A4和拟牛顿混合遗传算法A3、传统拟牛顿法A2。传统拟牛顿法A2只能找到方程组的一个实数根，说明其搜

教师叙事探究确实承担“集智”的重要价值，“集智”对于教师的专业成长意义显然。展示性的叙事分享对于“集智”确实有重要贡献，但是对于参与者的实质成长却存在阻隔。静听者倾向于对外归因，觉得自己没有遇上生命中的重要贵人，学生和家长又不配合，平时已经竭尽全力了，哪有时间读书和尝试改变，等等。因此，许多教师培训会知行分离，听者往往当场深受震撼，做起来却可能一筹莫展。

图1 5种算法的搜索能力

索能力极差。粒子群算法A4和拟牛顿混合遗传算法A3能够搜索方程组的两个实数根(该方程组只有

两个实数根)，说明粒子群算法A4和拟牛顿混合遗传算法A3在实数域的搜索能力尚可，但无法识别复数根。NGEA算法A5可以搜索到两个实数根和两个复数根，说明NGEA算法A5在实数域的搜算能力颇佳，对于复数域的搜索亦具有一定能力。综上所述，算法A1的搜索能力最强。

4.2 计算精度

(20)

利用数学知识可知，式(20)共2组实数解。利用5种算法分别进行计算，结果见表1。

表1 5种算法的计算精度

根据表1可以看出，算法A1、拟牛顿混合遗传算法A3、粒子群算法A4、NGEA算法A5可以搜索到所有解，但传统拟牛顿法A2只能搜索到一个解。

定义误差

(21)

为了更好地观察误差，将误差的单位设置成10-4(见图2)。

根据图2，本文提出的算法A1的精度最高，最高误差不超过3×10-7，最小误差为7×10-9，平均误差为6×10-8；传统拟牛顿法A2的精度相对较低，最高误差不超过83×10-4，最小误差为57×10-4，平均误差为6×10-3；粒子群算法A4和拟牛顿混合遗传算法A3的收敛精度相当，最高误差不超过98×10-4，最小误差为13×10-4，平均误差为21×10-4；NGEA算法A5精度也相对较低，最高误差不超过58×10-4，最小误差为11×10-4，平均误差为16×10-4。总体而言，本文提出的算法A1的精度是传统拟牛顿法A2的10 594.602 99倍，是拟牛顿混合遗传算法A3的22 183.721 19倍，是粒子

群算法A4的73 129.744 86倍，是NGEA算法A5的26 268.005 51倍。

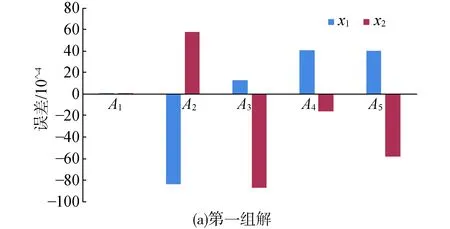
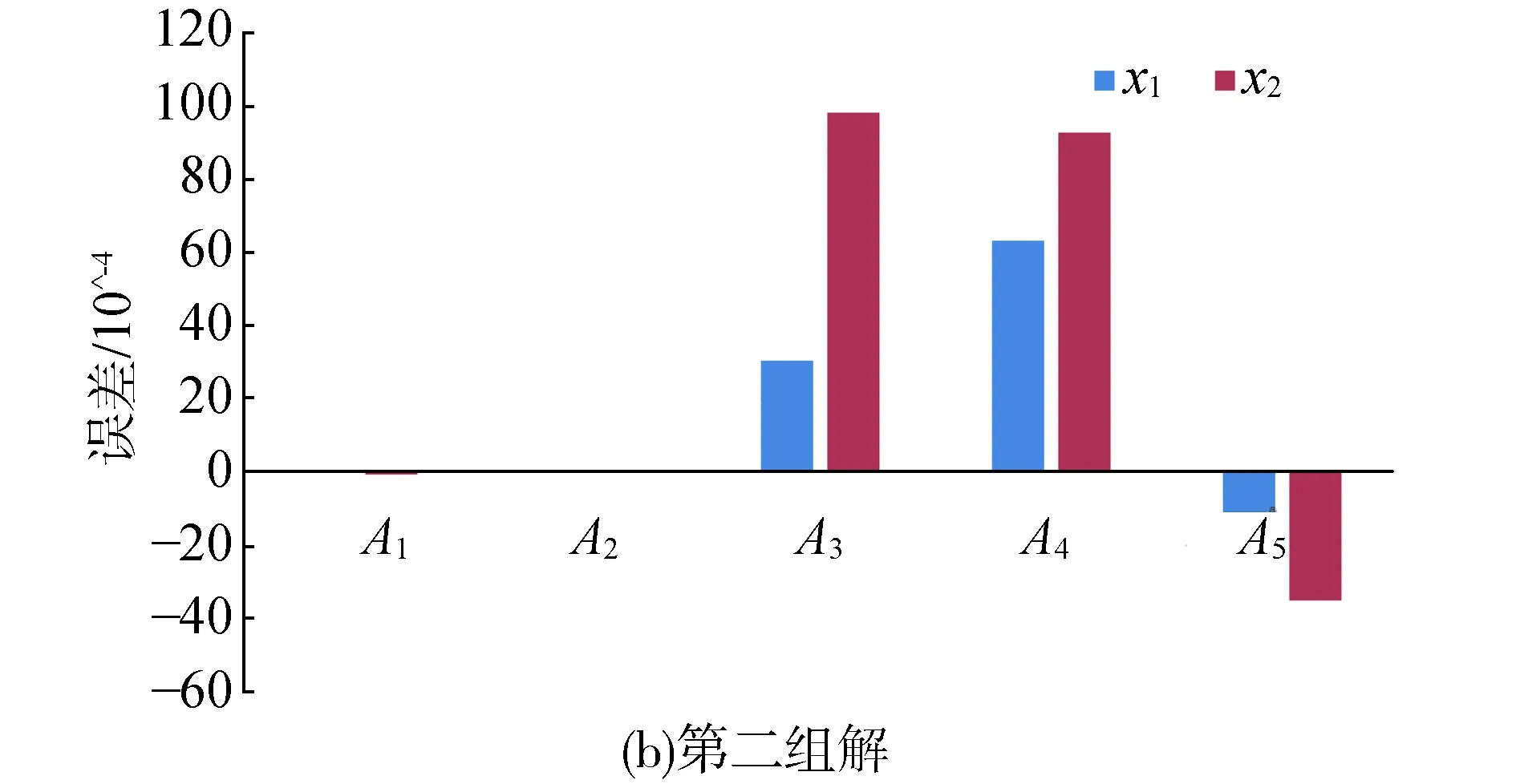
图2 5种算法的搜索能力

4.3 计算速度

(22)

利用5种算法分别进行计算，记录其计算耗时，计算设备的配置参数为：Pentium (R)Dual-Core CPU，2.2 GHz，2 G内存，win7X86系统。

根据图3，算法A1的计算速度最高，耗时为3.165 42 h；传统拟牛顿法A2的计算速度次之，耗时为4.675 62 h；NGEA算法A5计算速度最慢，耗时为14.586 77 h。总体而言，算法A1的计算速度是传统拟牛顿法A2的1.477 09倍，是拟牛顿混合遗传算法A3的3.403 61倍，是粒子群算法A4的3.052 63倍，是NGEA算法A5的4.608 16倍。

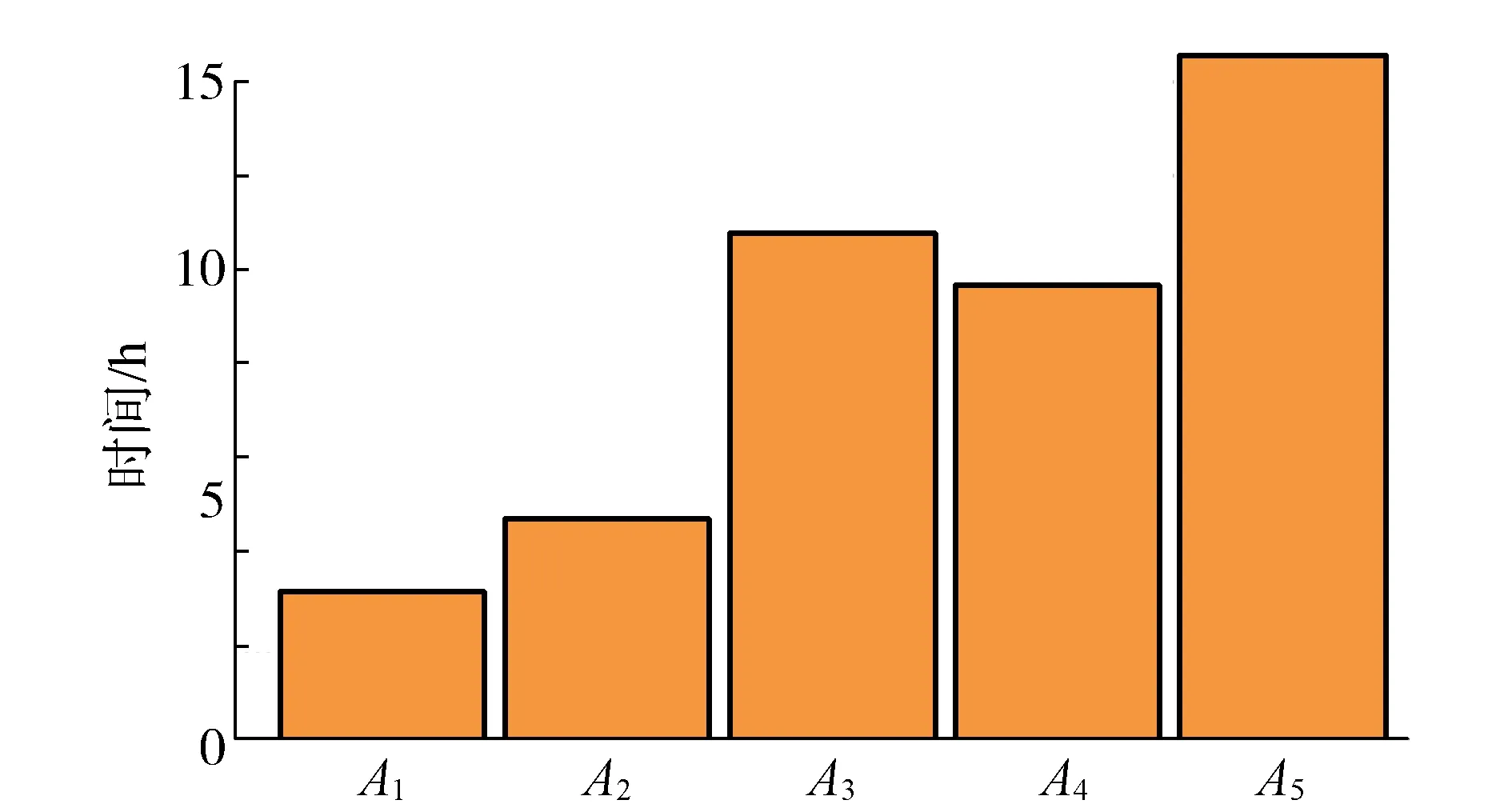
图3 5种算法的计算耗时

5 结 论

本文基于机器学习的思想，融合了半解析解的思想求解非线性方程组，得到一个精确度较高的解。与常用算法进行对比，结果发现：

1)算法A1的搜索能力最强，可以搜索出所有的解。

2)算法A1的精度是传统拟牛顿法A2的10 594.602 99倍，是拟牛顿混合遗传算法A3的22 183.721 19倍，是粒子群算法A4的73 129.744 86倍，是NGEA算法A5的26 268.005 51倍。

3)算法A1的计算速度是传统拟牛顿法A2的1.477 09倍，是拟牛顿混合遗传算法A3的3.403 61倍，是粒子群算法A4的3.052 63倍，是NGEA算法A5的4.608 16倍。

机器学习的思想是一种新的智能算法，可以对现有问题进行自动优化，对于提升计算效率、提高计算速度具有重要影响。

[1] EISEN M, MOKHTARI A, RIBEIRO A. A Decentralized Quasi-Newton Method for Dual Formulations of Consensus Optimization[J]. 2016.

[2] BALEEIRO A C, PEREIRA R P, BRIGATTO G A, et al. Multilayer Stratification Earth by Kernel Function and Quasi-Newton Method[J]. IEEE Latin America Transactions, 2016, 14(1):225-234.

[3] NIE Y, CHUNG C Y, XU N Z. System State Estimation Considering EV Penetration With Unknown Behavior Using Quasi-Newton Method[J]. IEEE Transactions on Power Systems, 2016:1-11.

[4] EISEN M, MOKHTARI A, RIBEIRO A. Decentralized Quasi-Newton Methods[J]. 2016.

[5] STELLA L, THEMELIS A, PATRINOS P. Forward-backward quasi-Newton methods for nonsmooth optimization problems[J]. 2016.

[6] YOUSEFIAN F, NEDI A, SHANBHA U V. Stochastic quasi-Newton methods for non-strongly convex problems: convergence and rate analysis[J]. 2016.

[8] RAHPEYMAII F, KIMIAEI M, BAGHERI A. A limited memory quasi-Newton trust-region method for box constrained optimization[J]. Journal of Computational and Applied Mathematics, 2016, 303:105-118.

[9] KITAGAWA J, MÉRIGOT Q, THIBERT B. A Newton algorithm for semi-discrete optimal transport[J]. 2016.

[10] 王俊奇, 李闯, 董晔. Bishop法的半解析解及其广义数学模型[J]. 水利与建筑工程学报, 2015(6):123-128.

[11] DASGUPTA S. Evaluation of the antimicrobial activity of Moringa oleifera seed extract as a sustainable solution for potable water[J]. Rsc Advances, 2016, 6.

[12] DASGUPTA A, POCO J, BERTINI E, et al. Reducing the Analytical Bottleneck for Domain Scientists: Lessons from a Climate Data Visualization Case Study[J]. Computing in Science & Engineering, 2016, 18(1):92-100.

[责任编辑：郝丽英]

Solutions to nonlinear equations based on machine learning theory

XU Lin

(Yangquan Techers College, Yangquan 045200,China)

In order to solve the problem of computational complexity, long calculation time and inaccurate calculation results in the process of solving nonlinear equations, this paper chooses machine learning method and Bayes rules to realize the decision-making and learning process for machine learning, by compromising the idea of semi-analytical solution, and developing real/complex solution procedure of nonlinear equations-“GuessKey”, in order to realize the search for all real solutions and complex solutions to nonlinear equations. Compared with the algorithm for solving the nonlinear equations which is commonly used in the present, the result shows this algorithm is superior to other algorithms in terms of global search capability, computational accuracy and computational speed.

Bayes rules; decision function; semi-analytical solution; computational accuracy

10.19352/j.cnki.issn1671-4679.2016.06.011

2016-06-30

徐 林(1982-)，女，讲师，研究方向：概率统计.

O241.7

A

1671-4679(2016)06-0045-04